Определяем основные геометрические размеры шестерни и колеса
Определяем делительные диаметры
Шестерни: d1 = z1 x m = 2 x 20 = 40 мм
Колеса: d2 = z2 x m = 80 x 2 = 160 мм
Определяем диаметры вершин зубьев
Шестерни: dа1 = d1 + 2 x m = 40 + 2 x 2 = 44 мм
Колеса: dа2 = d2 + 2 x m = 160 + 2 x 2 = 164 мм
Определяем диаметры впадин
Для прямозубых цилиндрических передач:
Шестерня: df1 = d1 – 2,5 x m = 40 – 2,5 x 2 = 35 мм
Колесо: df2 = d2 – 2,5 x m = 160 – 2,5 x 2 = 155 мм
Определяем высоту зуба
h = 2,25 x m = 2,25 x 2= 4,5 мм
Определяем ширину венца шестерни и колеса
Рабочая ширина венца b2 = 0,4 x 100 = 40 мм
b1 = (2…5) + b2 = 45 мм.
Проверяем величину межосевого расстояния
aw = 0,5 (d1 + d2) = 0,5 (40 + 160) =100 мм
Проверочный расчет закрытой передачи.
Проверка контактной выносливости рабочих поверхностей зубьев колес. Расчетом должна быть проверена справедливость соблюдения неравенства:
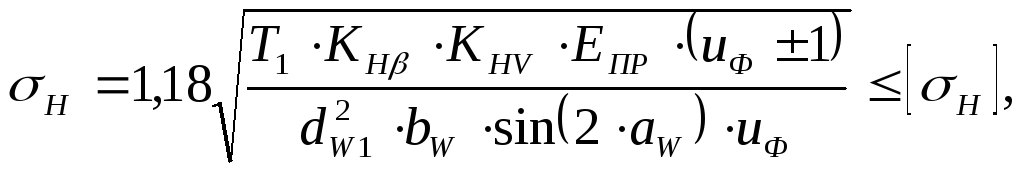
Т1 – вращающий момент на шестерне, Н мм;
КН
- коэффициент неравномерности распределения
нагрузки по длине контакта;
КНV – коэффициент внутренней динамической нагрузки;
ЕПР – приведенный модуль упругости, МПа;
uФ – фактическое передаточное число;
dW – начальный диаметр колеса, мм;
bW – рабочая ширина зубчатого венца колеса, мм;
aW – фактическое межосевое расстояние, мм 1.
bW =ba aW =0.4x100 = 40мм
Величину вращающего момента Т1 на шестерне определяем по формуле:
где - КПД передачи, принимаем = 0,96 1.
Коэффициент неравномерности нагрузки по длине контакта КН выбирают в соответствии с расположением колес относительно опор и твердостью рабочих поверхностей зубьев колес по графику, приведенному в 1: КН = 1,1.
Для определения коэффициента внутренней динамической нагрузки КНV необходимо рассчитать окружную скорость в зацеплении V, м/с:
В зависимости от значения V по таблице, приведенной в 1, назначаем степень точности передачи – 8. Затем определяем коэффициент внутренней динамической нагрузки КНV = 1,1.
Подставив численные значения в формулу (1.31) получим:
Допускаемое
контактное напряжение
,
т. е. неравенство не соблюдается:Н
> Н.
В результате проверки выявилась существенная недогрузка 10 %, то с целью более полного использования возможностей материалов зубчатых колес возможна корректировка рабочей ширины зубчатого венца по формуле:
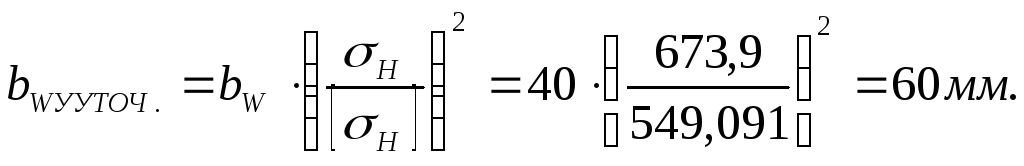
σH нов =550≤549,09МПа
Проверка прочности зубьев по напряжениям изгиба. Проверяют справедливость соотношения расчетных напряжений изгиба F и допускаемых напряжений F :
Ft – окружное усилие в зацеплении колес, Н;
КF - коэффициент неравномерности распределения нагрузки по длине контакта;
КFV – коэффициент внутренней динамической нагрузки;
YF1,2 – коэффициент формы зуба 1.
Окружное усилие в зацеплении колес Ft определяем по формуле:
Коэффициент неравномерности нагрузки по длине контакта КF выбирают в соответствии с расположением колес относительно опор и твердостью рабочих поверхностей зубьев колес по графику, приведенному в 1: КF = 1,05.
В зависимости от значения окружной скорости V по таблице, приведенной в 1, назначаем степень точности передачи – 8. Затем определяем коэффициент внутренней динамической нагрузки КFV = 1,1.
YF1,2 – коэффициент формы зуба определяем по графику 8.20 [2]
YF1=4,14;
YF2=3,72.
Подставив численные значения в формулу найдем значения расчетных напряжений изгиба F:
Допускаемые напряжения изгиба: F1 = 193,8 МПа; F2 = 212,148 МПа, неравенство соблюдается.