Достаточные признаки возрастания и убывания функции.
На основании достаточных признаков находятся промежутки возрастания и убывания функции. Вот формулировки признаков:
если производная функции y = f(x) положительна для любого x из интервала X, то функция возрастает на X;
если производная функции y = f(x) отрицательна для любого x из интервала X, то функция убывает на X.
Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:
найти область определения функции;
найти производную функции;
решить неравенства
и
на
области определения;к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.
Наибольшее
и наименьшее значение функции.С
практической точки зрения наибольший
интерес представляет использование
производной для нахождения наибольшего
и наименьшего значения функции. С чем
это связано? Максимизация прибыли,
минимизация издержек, определение
оптимальной загрузки оборудования...
Другими словами, во многих сферах жизни
приходится решать задачи оптимизации
каких-либо параметров. А это и есть
задачи на нахождение наибольшего и
наименьшего значения функции.
Наибольшим
значением функции y
= f(x)
на промежутке X
называют такое значение
,
что для любого
справедливо
неравенство
.
Наименьшим
значением функции y
= f(x)
на промежутке X
называют такое значение
,
что для любого
справедливо
неравенство
.
Эти
определения интуитивно понятны:
наибольшее (наименьшее) значение функции
– это самое большое (маленькое) принимаемое
значение на рассматриваемом интервале
при абсциссе
.
Стационарные
точки
– это значения аргумента, при которых
производная функции обращается в
ноль.
На
отрезке
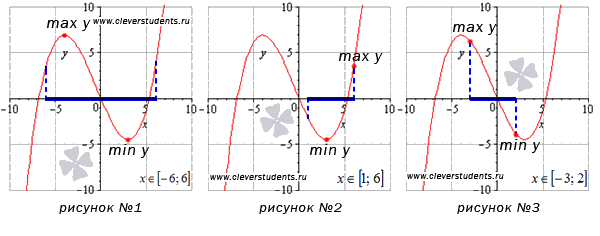
На первом рисунке функция принимает наибольшее (max y) и наименьшее (min y) значения в стационарных точках, находящихся внутри отрезка [-6; 6]. Рассмотрим случай, изображенный на втором рисунке. Изменим отрезок на [1; 6]. В этом примере наименьшее значение функции достигается в стационарной точке, а наибольшее - в точке с абсциссой, соответствующей правой границе интервала. На рисунке №3 граничные точки отрезка [-3; 2] являются абсциссами точек, соответствующих наибольшему и наименьшему значению функции.
15. Выпуклость, вогнутость и точки перегиба функции
Вторая производная. Если производная f ' ( x ) функции f ( x ) дифференцируема в точке ( x0 ), то её производная называется второй производной функции f ( x ) в точке ( x0 ), и обозначается f '' ( x0 ).
Функция
f
(
x
)
называется
выпуклой
на
интервале (
a,
b
),
если её график на этом интервале лежит
ниже
касательной,
проведенной к кривой
y
= f (
x
)
в любой точке (
x0
,
f
(
x0
) ), x0
(
a,
b
).
Функция f ( x ) называется вогнутой на интервале ( a, b ), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f ( x ) в любой точке ( x0 , f ( x0 ) ), x0 ( a, b ).
Достаточное условие вогнутости ( выпуклости ) функции.
Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:
если f '' ( x ) > 0 для любого x ( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );
если f '' ( x ) < 0 для любого x ( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) .
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба x0 существует вторая производная f '' ( x0 ), то f '' ( x0 ) = 0.
П р и м е р . |
Рассмотрим график функции y = x3 :
Эта функция является вогнутой при x > 0 и выпуклой при x < 0. В самом деле, y'' = 6x, но 6x > 0 при x > 0 и 6x < 0 при x < 0, следовательно, y'' > 0 при x > 0 и y'' < 0 при x < 0, откуда следует, что функция y = x3 является вогнутой при x > 0 и выпуклой при x < 0. Тогда x = 0 является точкой перегиба функции y = x3. |
Асимптоты функции
Асимптотой функции называют прямую, к которой приближаются точки графика функции при бесконечном удалении их от начала координат.
Вертикальные асимптоты
Вертикальные асимптоты определяются точками разрыва функции и границами области определения. График функции, непрерывной на всей числовой прямой, вертикальных асимптот не имеет. Некоторые особенности поведения функции в окрестности вертикальных асимптот представлено на рисунке. Вертикальные асимптоты определяются точками разрыва второго рода
Горизонтальные асимптоты
Если
,
то у = b — горизонтальная асимптота кривой y = f (x) (правая – при х стремящемуся к плюс бесконечности, левая – при х стремящемуся к минус бесконечности и двусторонняя, если пределы при х стремящемуся к плюс-минус бесконечности равны).
Рис.
8.3. Примеры горизонтальных двухсторонних
и односторонних асимптот
Наклонные асимптоты
Уравнение наклонной асимптоты функции y = f (x) определим уравнением y =k·x + b. При этом параметры наклонной асимптоты определяются соотношениями
,
.
Для
того, чтобы функция y
= f
(x
) имела асимптоту y
= k ·x + b,
н
еобходимо
и достаточно, чтобы существовали
указанные выше конечные пределы.
Общее исследование функции и построение графика
С помощью дифференциального исчисления можно установить характерные особенности изменения функций: возрастание и убывание, максимумы и минимумы, направление вогнутости графика, наличие асимптот. Обычно используют следующую схему исследования функций:
Определение области определения.
Определение четности или нечетности.
Определение периодичности функции.
Определение интервалов знака постоянства первой производной.
Определение интервалов знака постоянства второй производной.
Составление таблицы результатов.
х
у '
у ''
у
В первой строчке таблицы указываются интервалы, на которые разбивается область определения функции точками разрыва, точками экстремума и точками перегиба в порядке следования. Сами эти точки в порядке следования помещаются в отдельные столбцы. Во второй строчке таблицы в каждой ячейке указываются знаки первой производной. В третьей строчке таблицы в каждой ячейке указываются знаки второй производной. В четвёртой строчке определяется характер поведения функции в каждой ячейке. Если это точки экстремума или точки перегиба, то указываются значения функции в этих точках.
Нахождение асимптот.
Построение графика функции, начинается с построения асимптот и характерных точек.