13. (теорема Лагранжа). Если функция y=f(x) непрерывна на отрезке [ab] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [ab] найдется хотя бы одна точка c, a < c < b, что

f(b) - f(a) = f′(c) (b — a) (20.1)

Доказательство.

Обозначим и рассмотрим вспомогательную функцию F(x) = f(x) - f(a) - (x - a)Q. Эта функция удовлетворяет всем условиям теоремы Ролля: она непрерывна на [ab], дифференцируема на (ab) и F(a)=F(b)=0. Следовательно, на интервале (ab) есть точка с, в которой F′(c)=0. Но F′(x)=f′(x) — Q, то есть F′(c) = f′(c) — Q. Подставив в это равенство значение Q, получим

откуда непосредственно следует утверждение теоремы.

Замечание. Геометрический смысл теоремы Лагранжа: на графике функции y = f(x) найдется точка, касательная в которой параллельна отрезку, соединяющему точки графика с абсциссами а и b.

Теорема Ролля

Пусть функция f (x) непрерывна на [a, b], дифференцируема на (a, b) и на концах отрезка принимает равные значения f(a) = f(b). Тогда существует точка c Î (a, b), в которой f ' (c) = 0.

Доказательство. Так как функция f(x) непрерывна на [a, b],то по свойству непрерывных функций она достигает на этом отрезке максимальное значение М и минимальное значение m.

Возможны два случая: максимум и минимум достигаются на концах отрезка или что – либо (или максимум, или минимум) попадает вовнутрь интервала. В первом случае f (x) = const = M = m. Поэтому производная равна нулю f ' (c) = 0 в любой точке отрезка [a, b], и теорема доказана.

Во втором случае, так как f (x) дифференцируема в точке c, из теоремы Ферма следует, что f ' (c) = 0.

Раскрытие неопределенностей.

Если функции f(x) и g(x) удовлетворяют на некотором отрезке [ab] условиям теоремы Коши и f(a) = g(a) = 0, то отношение f(x)/g(x) не определено при х=а, но определено при остальных значениях х. Поэтому можно поставить задачу вычисления предела этого отношения при x→a. Вычисление таких пределов называют обычно «раскрытием неопределенностей вида {0/0}».

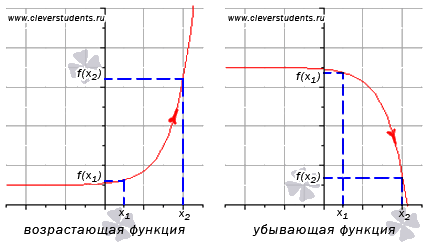
14. Определение возрастающей функции. Функция y = f(x) возрастает на интервале X, если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции. Определение убывающей функции. Функция y = f(x) убывает на интервале X, если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

ЗАМЕЧАНИЕ: если функция определена и непрерывна в концах интервала возрастания или убывания (a; b), то есть при x = a и x = b, то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке X. К примеру, из свойств основных элементарных функций мы знаем, что y = sinx определена и непрерывна для всех действительных значений аргумента. Поэтому, из возрастания функции синуса на интервале 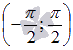мы можем утверждать о возрастании на отрезке . 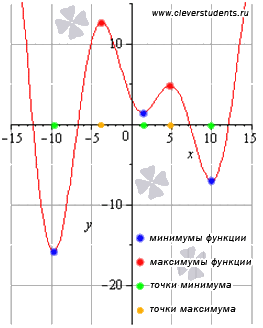Точку называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке максимума называют максимумом функции и обозначают . Точку называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают . Под окрестностью точки понимают интервал , где - достаточно малое положительное число. Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции.

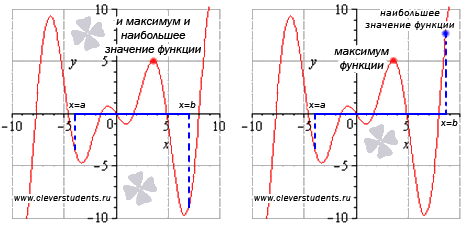
Не путайте экстремумы функции с наибольшим и наименьшим значением функции. На первом рисунке наибольшее значение функции на отрезке [a; b] достигается в точке максимума и равно максимуму функции, а на втором рисунке – наибольшее значение функции достигается в точке x = b, которая не является точкой максимума. \