15. Постулаты квантовой механики и описание динамических переменных с помощью операторов. Условие одновременной измеримости различных динамических переменных.

I постулат. Состояние движения квантового объекта описывается волновой функцией ψ.

Физический смысл волновой функции в том, что её квадрат есть плотность вероятности обнаружения частицы в данном квантовом состоянии. Плотность вероятности определяется так: , так как функция ψ комплексна. Тогда вероятность обнаружения частицы в данном квантовом состоянии, описываемом волновой функцией, будет: .

II постулат. Волновая функция ψ подчиняется волновому уравнению: . Здесь – оператор Гамильтона (полной энергии системы), а уравнение, сформулированное во втором постулате, называется уравнением Шредингера.

III постулат. Каждая динамическая переменная представляется определённым линейным эрмитовым оператором.

IV постулат. При изменении некоторой динамической переменной, описываемой оператором , с определённой вероятностью получается одно из собственных значений этого оператора. Вероятность измерения собственного значения равна , где есть коэффициент разложения волновой функции ψ по собственным функциям оператора : . Среднее значение динамической переменной, описываемой оператором в состоянии, описываемом волновой функцией ψ, определяется так: 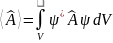. Условие одновременной измеримости различных динамических переменныхНеобходимым и достаточным условием того, чтобы две физические величины имели одновременно определённые значения, является коммутативность операторов, описывающих эти величины.

16. Соотношение неопределенностей. . Данное соотношение носит название соотношения неопределённостей Гейзенберга. Оно показывает, что импульс и координаты частицы не могут быть одновременно определены (измерены) со сколь угодно большой точностью, хотя любая из этих величин по отдельности измерима с любой точностью. До измерения частица не имела определённых значений динамических переменных. Определённые значения динамические переменные квантовой системы принимают только в процессе измерения.

17. Свободное движение частицы. Движение частицы на длине периодичности. : . общее уравнение Шредингера имеет однозначное и непрерывное решение, которое существует для любых значений , что означает, что энергия свободно движущейся частицы может принимать любые значения, то есть энергетический спектр непрерывен. Более того, энергия частицы и её импульс являются величинами одновременно измеримыми, то есть . Движение частицы на длине периодичности.Пусть само по себе движение частицы неограничено, но нас интересует движение частицы на участке L. В этом случае мы можем рассматривать не всё бесконечное пространство, а участок длиной L. Пусть вне этого участка значения волновой функции повторяются, то есть волновая функция периодична с периодом L. Условие периодичности мы можем записать в виде: . Так как движение ограничено, то спектр энергии может быть дискретен. Найдём все возможные значения энергии: . Условие периодичности нам даёт следующее выражение: , где . Очевидно, что данное равенство возможно, если 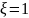. Распишем эту экспоненту: 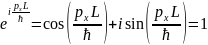. Отсюда , . Таким образом, импульс принимает какие-то строго определённые значения, значит, и энергия тоже принимает определённые дискретные значения: 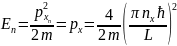. . Величина называется шагом дискретизации энергии. Найдём расстояние между энергетическими уровнями: . Из последней формулы видно, что расстояния между энергетическими уровнями обратно пропорциональны . Таким образом, чем конкретнее и меньше L, тем разрежённей энергетические уровни. При спектр, очевидно, становится непрерывным. Обобщая предыдущие рассуждения, можно сказать: чем точнее локализовано положение частицы. Тем ярче выражена дискретность её спектра.

18. Частица в одномерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками. Рассмотрим простейший случай одномерной потенциальной ямы с бесконечно высокими стенками. Её можно описать следующими уравнениями: . Стационарное уравнение Шредингера внутри ямы имеет вид: . Здесь – энергия частицы. Граничные условия: . Введём следующее обозначение: . Тогда уравнение Шредингера примет вид: . Решением данного уравнения является функция 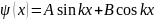. Используем первое граничное условие: , следовательно, . Но , поэтому B=0. Применим теперь второе граничное условие: 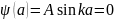. То есть . Получается, что k зависит от n. Тогда . Очевидно, что k принимает дискретные значения. Вспоминая, что , получим с учётом последнего выражения: 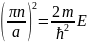. Отсюда , причём минимальная энергия равна: . Таким образом, энергию движущейся частицы внутри потенциальной ямы мы можем представить в виде энергетических уровней. Волновая функция такой частицы имеет вид: . Волновая функция основного состояния . Эта функция внутри ямы изменяется и с уменьшением размера ямы энергия возрастает. Найдём константу A из условия нормировки: вероятность нахождения частицы внутри ямы равна 1: . . Отсюда и для волновой функции имеем: . В случае конечных значений потенциальной энергии существует ненулевая вероятность прохождения частицы за пределы ямы.

19. Квантовый линейный гармонический осциллятор, энергия и волновые функции. Частица, совершающая гармонические колебания, называется гармоническим осциллятором. Уравнение Шредингера примет вид: , где , .

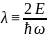. Минимальная энергия, которой может обладать квантовая частица, как следует из этого соотношения, будет . Эта энергия называется энергией вакуума (энергия нулевых колебаний).

Значение энергии: , , n – номер орбиты – главное квантовое число; l – орбитальное число; k – радиальное квантовое число.