13 Афчх сар

Если на вход элемента или всей системы подавать синусоидальные колебания с постоянной амплитудой и частотой, то после окончания переходного процесса на выходе возникают такие же синусоидальные колебания с такой же частотой, но другой амплитуды и фазы

Комплексная хар-ка вкл в себя АЧХ и ФЧХ наз АФЧХ

Синусоидальный сигнал можно представить в комплексной форме

АФЧХ строят на комплексной плоскости. Каждому значению частоты будет соответствовать точка на комплексной плоскости (мнимая и действительная ось)

АФЧХ легко получить из передаточной ф-ии путем замены р на jw

График АФЧХ наз годограф

14 Лачх и лфчх сар

ЛАЧХ - L(w) характеристика, построенная в логарифмическом масштабе частот по оси абсцисс и амплитуды по оси ординат

ЛФЧХ-φ(w) –хар-ка фазы сигнала от частоты, построенная в логарифмическом масштабе частот по оси абсцисс и в обычном масштабе по осси ординат.

При построении ЛАЧХ по оси абсцисс откладываются частоты в логарифмическом масштабе в декадах

Декада- интервал частот соответствующий измерению частоты в 10 раз

Единицей измерения амплитуды L(w) явл децибел

Единичным отрезком явл 20lg A(w)

15 Объекты с самовыравниванием и объекты без самовыравнивания

Самовыравнивание- это способность приходить после возмущения в новое установившееся состояние без вмешательства регулятора.

Объект с самовыравниванием наз Статическим.

А не обладающие самовыравниванием – Астатические

Без самовыравнивания

Самовыравнивание по стоку

Самовыравнивание по притоку

Самовыравнивание и по стоку и по притоку

Самовыравнивание объекта хар-ся коэф самовыравнивания

- относительный сток

- относительный приток

Если , то объект обладает идеальным самовыравниванием (гидравлический бак)

Если , то объект не обладает самовыравниванием

16. Идентификация объекта методом Симаю

Метод предназначен для идентификации объектов по экспериментальным данным кривой разгона.

Симаю предложил аппроксимировать S-образную ф-ию в виде передаточной ф-ии:

1. Находим коэффициент передачи объекта

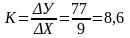
По кривой разгона заполняем таблицу:

t	y	ym-yi	z1	y1	z2
0	10	77	4,34	7,25	1,07
8	17,32	69,68	4,24	6,6	0,86
16	30,71	56,29	4,03	5,99	0,67
24	40,39	46,61	3,84	5,35	0,41
32	55,03	31,97	3,46	4,7	0,22
40	63,87	23,13	3,14	4,09	-
48	70,66	16,34	2,79	3,36	-
56	75,81	11,19	2,42	2,75	-
64	79,67	7,33	1,99	2,15	-
72	82,56	4,44	1,49	1,5	-
80	84,72	2,28	0,82	0,85	-
88	86,33	0,67	-	-	-
90	87,00	0	-	-	-

2. Находим координаты кривой z₁(t) по формуле:

Z₁= Ln(Ym-Y)= Ln(77)= 4,34

3) Строим кривую Z₁(t) и проводим касательную (~10%) к хвостовой части графика

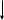Z₁

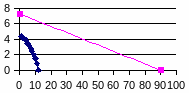Рисунок 1. Зависимость Z1(t)

4) Находим 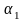– угол наклона касательной к оси t и постоянную времени T₁:

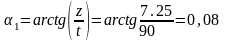
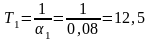
5) Находим площади S_1.1 – под касательной и S_1.2 – под кривой Z₁(t):

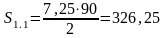
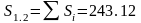
6) Определяем погрешность δ₁:

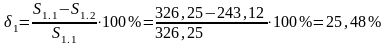
т.к. полученная погрешность больше допустимой 25,48% > 10%,то продолжаем расчет

7) Находим координаты кривой Z₂(t) по формуле:

Z₂(t)= Ln(Y1-Z1)= Ln(9,3-4,3)= 1,6

8) Строим кривую Z₂(t) и проводим касательную (~10%) к хвостовой части графика (Рисунок2):

Z₂

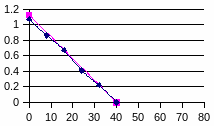
Рисунок 2. Зависимость Z2(t)

9) Находим 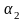– угол наклона касательной к оси t и постоянную времени T₂:

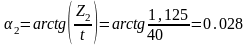
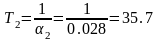
10) Находим площади S_2.1 – под касательной и S_2.2 – под кривой Z₂(t):

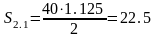
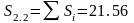
11) Определяем погрешность δ₂:

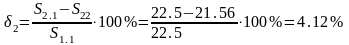
т.к. 4,12%<10% , то заканчиваем расчет.

12) Следовательно, кривая разгона имеет второй порядок и передаточная функция имеет вид: