Е

XoYплоскость колебаний, в ней колеблется вектор напряженности электрического поля

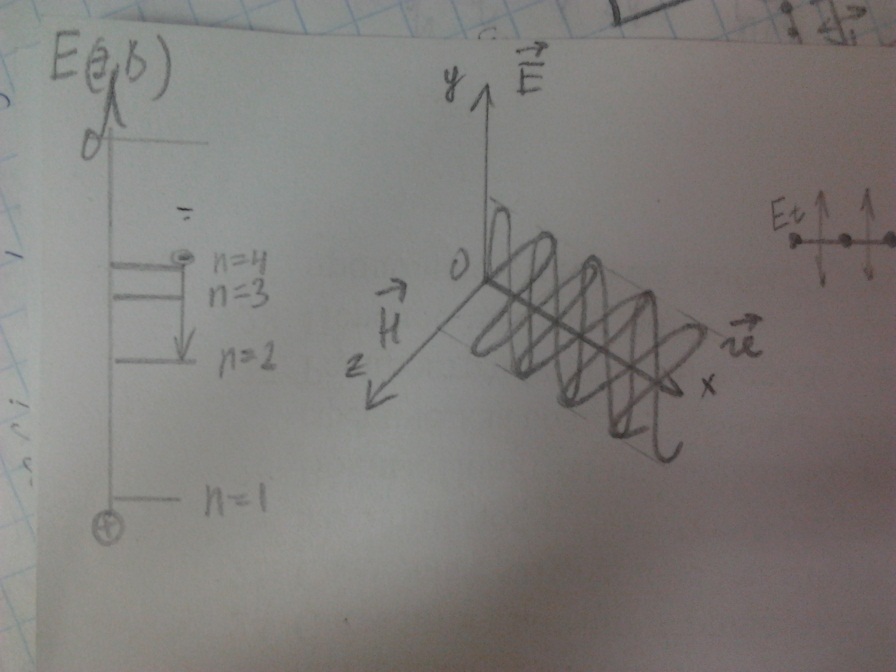
XOZ – плоскость поляризации, в ней колеблется вектор напряженности магнитного поля

Эта волна испускаемая одним электроном в атоме, где Е колеблется в одной плоскости называется плоскополяризованной

стественный свет состоит из бесчисленного множества элементарных волн («цугов») излучаемых отдельными электронами в атомах вещества. При их переходах из состояний с большей энергией в состояние с меньшей энергией, излучает при этом квант света, называемый элементарной волной или цугом.

Е стественный свет – это совокупность бесчисленного множества равновероятных ориентаций в пространстве вектора напряженностиЕ(плоскостей колебания Е) относительно скорости волны

Естественный свет обладает осевой симметрией:

Плоско поляризованный луч

Тоже, но перпендикулярно

Частично поляризованный (нормальных больше, чем тангенсальных)

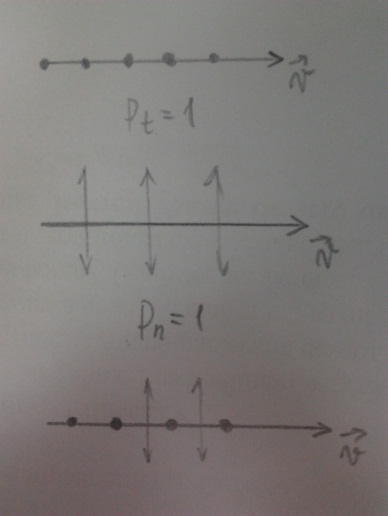
Явлением поляризации называется явление выделения из естественного света частичнополяризованного или плоскополяризованного луча.

P=(Y_max-Y_min)/(Y_max+Y_min)

Р– степень поляризации

Степень поляризации плоскополяризованной волны = 1 (Р=1)

Поляризатор, анализатор.

Поляризаторы – приборы, которые из естественного света выделяют свет частичнополяризованный или плоскополяризованный.

Анализатор в оптике - поляризатор, предназначенный для определения состояния поляризации света (степени поляризации, степени эллиптичности и т. п.) или для регистрации ее изменений.

Закон Малюса

Двойное лучепреломление закон Малюса. Наблюдается на испанском шпате – это кристаллы, которые имеют различный показатель преломления луча в различных направлениях. Но есть направление, вдоль которого луч света идет не преломляясь.

(обыкнов)

n₀=1,66

v₀=c/n₀

(необыкнов)

n_e=1,51 v_e=c/n_e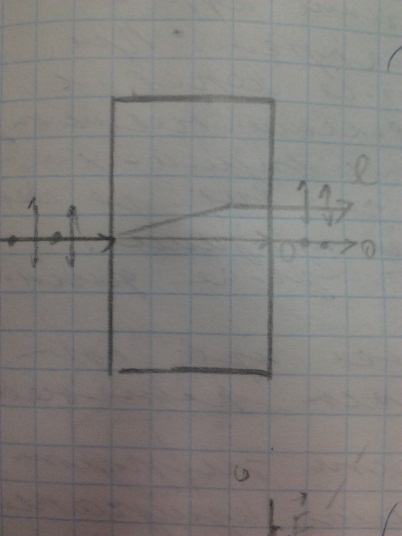

Закон Малюса — зависимость интенсивности линейно-поляризованного света после его прохождения через поляризатор от угла между плоскостями поляризации падающего света и поляризатора.

гдеI₀ — интенсивность падающего на поляризатор света, I — интенсивность света, выходящего из поляризатора.

Установлен Э. Л. Малюсом в 1810 году.

Свет с иной (не линейной) поляризацией может быть представлен в виде суммы двух линейно-поляризованных составляющих, к каждой из которых применим закон Малюса. По закону Малюса рассчитываются интенсивности проходящего света во всех поляризационных приборах, например в поляризационных фотометрах и спектрофотометрах. Потери на отражение, зависящие от и не учитываемые законом Малюса, определяются дополнительно.

Поляризация света при отражении и преломлении на границе двух диэлектриков

Если естественный свет падает на границу раздела двух диэлектриков (например, воздуха и стекла), то часть его отражается, а часть преломляется и распространяется во второй среде. Устанавливая на пути отраженного и преломленного лучей анализатор (например, турмалин), убеждаемся в том, что отраженный и преломленный лучи частично поляризованы: при поворачивании анализатора вокруг лучей интенсивность света периодически усиливается и ослабевает (полного гашения не наблюдается!). Дальнейшие исследования показали, что в отраженном луче преобладают колебания, перпендикулярные плоскости падения (они обозначены точками), в прелом ленном - колебания, параллельные плоскости падения (изображены стрелками).

Степень поляризации (степень выделения световых волн с определенной ориентацией электрического (и магнитного) вектора) зависит от угла падения лучей и показателя преломления. Шотландский физик Д. Брюстер (1781-1868) установил закон, согласно которому при угле падения ib (угол Брюстера), определяемого соотношением

(n21 - показатель преломления второй среды относительно первой), отраженный луч является плоскополяризованным (содержит только колебания, перпендикулярные плоскости падения). Преломленный же луч при угле падения iB поляризуется максимально, но не полностью.

Вопрос №37 Двойное лучепреломление. Одноосные кристаллы. Поляризационные призмы и поляроиды. Искусственная оптическая анизотропия. Вращение плоскости поляризации.

Двойное лучепреломление.

Двойно́е лучепреломле́ние — эффект расщепления в анизотропных средах луча света на две составляющие. Впервые обнаружен на кристалле исландского шпата. Если луч света падает перпендикулярно к поверхности кристалла, то на этой поверхности он расщепляется на два луча. Первый луч продолжает распространяться прямо, и называется обыкновенным(o — ordinary), второй же отклоняется в сторону, нарушая обычный закон преломления света, и называется необыкновенным (e — extraordinary).

;

;

Одноосные кристаллы.

• Отрицательные кристаллы — одноосные кристаллы, в которых скорость распространения обыкновенного луча света меньше, чем скорость распространения необыкновенного луча. В кристаллографии Отрицательными кристаллами называют также жидкие включения в кристаллах, имеющие ту же форму, что и сам кристалл.

• Положительные кристаллы — одноосные кристаллы, в которых скорость распространения обыкновенного луча света больше, чем скорость распространения необыкновенного луча

Поляризационные призмы и поляроиды.

В основе работы поляризационных приспособлений, служащих для получения поляризованного света, лежит явление двойного лучепреломления. Наиболее часто для этого применяются призмы и поляроиды. Призмы делятся на два класса:

1) призмы, дающие только плоскополяризованный луч (поляризационные призмы);

2) призмы, дающие два поляризованных во взаимно перпендикулярных плоскостях луча (двоякопреломляющие призмы).

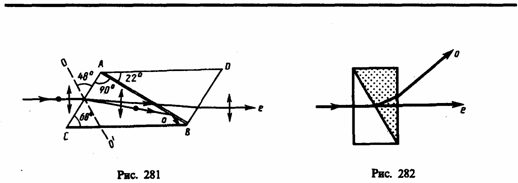
Поляризационные призмы построены по принципу полного отражения одного из лучей (например, обыкновенного) от границы раздела, в то время как другой луч с другим показателем преломления проходит через эту границу. Типичным представителем поляризационных призм является призма Николя, называемая часто николем. Призма Николя (рис. 281) представляет собой двойную призму из исландского шпата, склеенную вдоль линии АВ канадским бальзамом сп=1,55. Оптическая ось ОО' призмы составляет с входной гранью угол 48°. На передней грани призмы естественный луч, параллельный ребру СВ,раздваивается на два луча: обыкновенный (n_о=1,66) и необыкновенный (n_e=1,51). При соответствующем подборе угла падения, равного или большего предельного, обыкновенный луч испытывает полное отражение (канадский бальзам для него является средой оптически менее плотной), а затем поглощается зачерненной боковой поверхностью СВ. Необыкновенный луч выходит из кристалла параллельно падающему лучу, незначительно смещенному относительно него (ввиду преломления на наклонных гранях АС и BD). 

Двояко преломляющие призмы используют различие в показателях преломления обыкновенного и необыкновенного лучей, чтобы развести их возможно дальше друг от друга. Примером двояко преломляющих призм могут служить призмы из исландского шпата и стекла, призмы, составленные из двух призм из исландского пшата со взаимно перпендикулярными оптическими осями. Для первых призм (рис. 282) обыкновенный луч преломляется в шпате и стекле два раза и, следовательно, сильно отклоняется, необыкновенный же луч при соответствующем подборе показателя преломления стекла n (n»n_e) проходит призму почти без отклонения. Для вторых призм различие в ориентировке оптических осей влияет на угол расхождения между обыкновенным и необыкновенным лучами.

Двояко преломляющие кристаллы обладают свойством дихроизма, т. е. различного поглощения света в зависимости от ориентации электрического вектора световой волны, и называются дихроичными кристаллами. Примером сильно дихроичного кристалла является турмалин, в котором из-за сильного селективного поглощения обыкновенного луча уже при толщине пластинки 1 мм из нее выходит только необыкновен­ный луч. Такое различие в поглощении, зависящее, кроме того, от длины волны, приводит к тому, что при освещении дихроичного кристалла белым светом кристалл по разным направлениям оказывается различно окрашенным.

Дихроичиые кристаллы приобрели еще более важное значение в связи с изобретени­ем поляроидов. Примером поляроида может служить тонкая пленка из целлулоида, в которую вкраплены кристаллики герапатита (сернокислого иод-хинина). Герапатит — двояко преломляющее вещество с очень сильно выраженным дихроизмом в об­ласти видимого света. Установлено, что такая пленка уже при толщине »0,1 мм полностью поглощает обыкновенные лучи видимой области спектра, являясь в таком тонком слое совершенным поляризатором. Преимущество поляроидов перед призмами — возможность изготовлять их с площадями поверхностей до нескольких квадрат­ных метров. Однако степень поляризации в них сильнее зависит от l, чем в призмах. Кроме того, их меньшая по сравнению с призмами прозрачность (приблизительно 30%) в сочетании с небольшой термостойкостью не позволяет использовать поляро­иды в мощных световых потоках. Поляроиды применяются, например, для защиты от ослепляющего действия солнечных лучей и фар встречного автотранспорта.

Искусственная оптическая анизотропия.

Двойное лучепреломление имеет место в естественных анизотропных средах. Существуют, однако, различные способы получения искусственной оптической анизотропии, т. е. сообщения оптической анизотропии естественно изотропным веществам.

Оптически изотропные вещества становятся оптически анизотропными под действием:

1) одностороннего сжатия или растяжения (кристаллы кубической системы, стекла и др.);

2) электрического поля (эффект Керра; жидкости, аморфные тела, газы);

3) магнитного поля (жидкости, стекла, коллоиды).

В перечисленных случаях вещество приобретает свойства одноосного кристалла, оптическая ось которого совпадает с направлением деформации, электрического или магнитного полей соответст­венно указанным выше воздействиям. 

Мерой возникающей оптической анизотропии служит разность показателей прело­мления обыкновенного и необыкновенного лучей в направлении, перпендикулярном оптической оси:

,где k₁, k₂, k₃ — постоянные, характеризующие вещество, s — нормальное напряжение, Е и Н — соответственно напряженность электрического и магнитного полей.

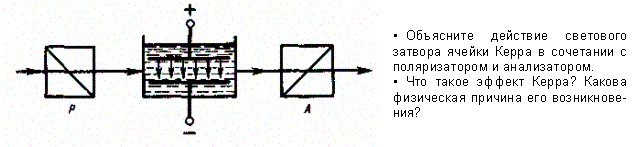
На рис. 284 приведена установка для наблюдения эффекта Керра в жидкостях (установки для изучения рассмотренных явлений однотипны). Ячейка Керра — кювета с жидкостью (например, нитробензолом), в которую введены пластины конденсатора, помещается между скрещенными поляризатором Р и анализатором А. При отсутствии электрического поля свет через систему не проходит. При наложении электрического поля жидкость становится двояко преломляющей; при изменении разности потенци­алов между электродами меняется степень анизотропии вещества, а следовательно, и интенсивность света, прошедшего через анализатор. На пути l между обыкновенным и необыкновенным лучами возникает оптическая разность хода

или соответственно разность фаз

где B=k₂/l — постоянная Керра.

Эффект Керра — оптическая анизотропия веществ под действием электрического поля — объясняется различной поляризуемостью молекул жидкости по разным направлениям. Это явление практически безынерционно, т. е. время перехода вещества из изотропного состояния в анизотропное при включении поля (и обратно) составляет приблизительно 10^–10 с. Поэтому ячейка Керра служит идеальным световым затвором и применяется в быстропротекающих процессах (звукозапись, воспроизводство звука, скоростная фото- и киносъемка, изучение скорости распространения света и т. д.), в оптической локации, в оптической телефонии и т. д.

Искусственная анизотропия под действием механических воздействий позволяет исследовать напряжения, возникающие в прозрачных телах. В данном случае о степени деформации отдельных участков изделия (например, остаточных деформаций в стекле при закалке) судят по распределению в нем окраски. Так как применяемые обычно в технике материалы (металлы) непрозрачны, то исследование напряжений производят на прозрачных моделях, а потом делают соответствующий пересчет на проектируемую конструкцию.

Вращение плоскости поляризации света, поворот плоскости поляризации линейно поляризованного света при его прохождении через вещество. Вращение плоскости поляризации наблюдается в средах, обладающих двойным круговым лучепреломлением, т. е. различными показателями преломления для право- и левополяризованных по кругу лучей. Линейно поляризованный пучок света можно представить как результат сложения двух лучей, распространяющихся в одном направлении и поляризованных по кругу с противоположными направлениями вращения. Если такие два луча распространяются в теле с различными скоростями, то это приводит к повороту плоскости поляризации суммарного луча. Вращение плоскости поляризации может быть обусловлено либо особенностями внутренней структуры вещества, либо внешним полем. Вращение плоскости поляризации наблюдается, как правило, в оптически изотропных телах (кубические жидкости, растворы и газы). Явлением вращение плоскости поляризации пользуются для исследования структуры вещества и определения концентрации оптически-активных молекул (например, в растворах, а также в ряде оптических приборов, оптические модуляторы, затворы, вентили, квантовые гироскопы и т.п.).

Вопрос №38 Тепловое излучение. Его характеристики и законы. Квантовая гипотеза и формула Планка.

Тепловое излучение - это электромагнитное излучение, происходящее за счет внутренней

энергии теплового движения атомов и молекул вещества во всем спектральном

интервале.

Тепловое излучение свойственно всем вещества, температура которых выше 0 К.

Тепловое излучение - это единственное излучение, которое может быть равновесным -

если тело поглощает энергию в каком либо интервале, то точно так же энергия излучается

в этом же интервале длины волны и частоты. При этом если тело не поглощает, то при

этом оно и не излучает.

Характеристики теплового излучения:

1. Тепловое излучение характеризуется сплошным спектром.

При высоких температурах короткая длина волны при высоких частотах характерна для

видимого и ультрафиолетового излучения.

При низких температурах излучаются длинноволновые инфракрасные волны.

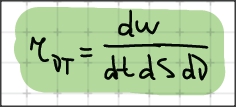
2) -- интегральная энергетическая светимость - это энергия электромагнитного излучения, испускаемая в единицу времени, единицу площади во всем спектральном интервале.

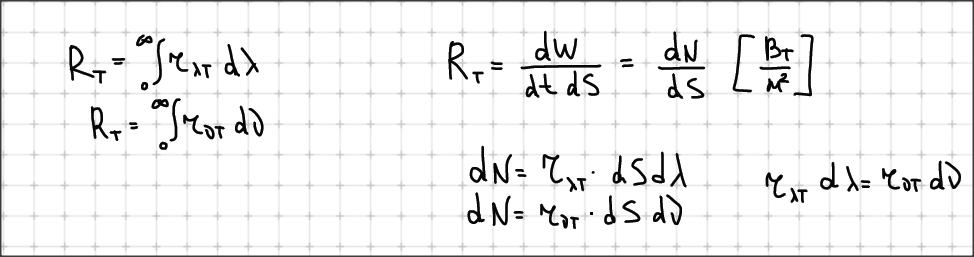
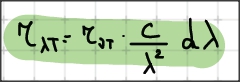
2. Спектральная поглощательная способность.

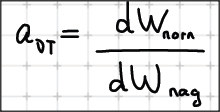-в единичном интервале частот, на единицу площади,

за единицу времени.

Основные законы теплового излучения.

1. Закон Кирхгофа.

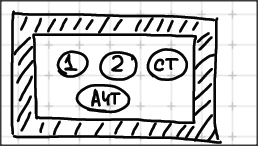
Серое тело - это тело, поглощательная способность которого меньше

единицы, но одинакова для всех частот и зависит только от

температуры, материала и состояния поверхности.

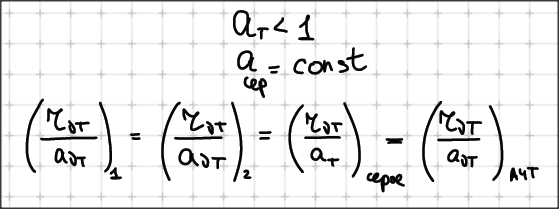
Отношение спектральной способности энергетической светимости

к спектральной поглощаемой способности не зависит от природы тела и является для

всех тел универсальной формулой частоты и температуры.

2. Закон Стефана-Больцмана.

О н определяет энергетическую светимость.

Энергетическая светимость для абсолютно чёрного тела = постоянной Больцмана умноженной на температуру в 4 степени.

3. Первый закон смещения Вина.

Длина волн, на которые приходится максимальная плотность энергетической светимости АЧТ

обратно-пропорционально термодинамической температуре. Этот закон объясняет, почему при

охлаждении нагретых тел в их спектре преобладает длиноволновое излучение.

4. Второй закон Вина.

5. Формула Рэлея и Джинса.

Формула Рилэя и Джинса является частным случаем формулы Планка при высоких температурах.

6. 14 декабря 1900 год – Планк предложил:

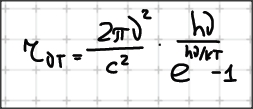
При высоких температурах kT>h*«ню», и тогда формула Планка примет вид:

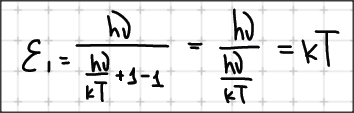
Вопрос №39 Фотоэффект, его законы. Энергия, масса импульс фотона. Эффект Комптона.

Явление фотоэффекта - явление вырывания электронов с поверхности металла под действием квантов света.

На рисунке показана схема установки для изучения внешнего фотоэффекта в металлах. Свет падает через окно D на поверхность катода К, находящегося внутри эвакуированной трубки и называемого фотокатодом. Характер зависимости фототока I в трубке от разности потенциалов U анода А и катода К при постоянной энергетической освещенности Е_э катода монохроматическим светом изображен на рисунке 2.

Существование фототока при отрицательных значениях U от 0 до-U₀ свидетельствует о том, что фотоэлектроны выходят из катода, имея некоторую начальную скорость и соответственно кинетическую энергию. Максимальная начальная скорость фотоэлектронов υ_макс связана с задерживающим напряжением (задерживающим потенциалом ) U₀соотношением

, Где е и m-абсолютная величина заряда и масса электрона.

Фототок увеличивается с ростом U лишь до определенного предельного значения I_н, называемого фототоком насыщения . При фототоке насыщения все электроны , вылетающие из катода под влиянием света , достигают анода. Если n_сек-число фотоэлектронов , покидающих катод за 1с, то

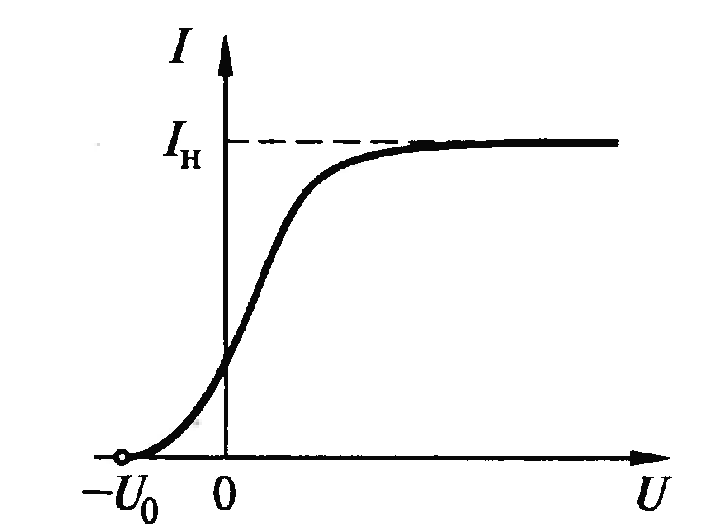
Рис 2

Законы фотоэффекта.

1.максимальная начальная скорость фотоэлектронов определяется частотой света и не зависит от его интенсивности.

2.Для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота ν₀ света, при которой еще возможен фотоэффект(ν₀ зависит от химической природы вещества и состояния его поверхности)

3. Число фотоэлектронов n, вырываемых из катода за единицу времени , пропорционально интенсивности света , т.е. фототок насыщения пропорционален энергетической освещенности Е катода(закон Столетова)

А. Эйнштейн показал, что все закономерности фотоэффекта объясняются, если предположить, что свет поглощается такими же порциями (квантами, фотонами), какими он по гипотезе Планка испускается. Согласно Эйнштейну, энергия фотона E=hν , полученная электроном, усваивается им целиком. Рассмотрим с квантовой точки зрения фотоэффект в металлах. Электрон удерживается в металле притяжением положительных ионов кристаллической решетки. Для того, чтобы покинуть металл, электрон должен совершить работу выхода Aвых . Если полученная электроном энергия E = hν > Aвых , то он при вылете будет обладать кинетической энергией. Величина этой энергии максимальна, если электрон покидает металл с поверхности, а не с какой-то глубины. В этом случае в соответствии с законом сохранения энергии выполняется соотношение, которое называется уравнением Эйнштейна для внешнего фотоэффекта:

E = hν = Aвых +W max ; W_max=mυ²/2;

Из формулы Эйнштейна видно, что фотоэффект с поверхности данного вещества наблюдается только при частотах, удовлетворяющих условию hν ≥ Aвых . Тогда красную границу фотоэффекта ( ν₀ или λ0 ) можно определить из уравнения hν₀ = Aвых

Энергия, масса импульс фотона

Фотон - ультрарелятивистская частица, так как он всегда движется со скоростью с света в вакууме. Это объясняется тем, что фотон имеет нулевую массу.

Импульс фотона p_f и его энергия W_f в соответствии с общей формулой теории относительности связаны соотношением

W_f=c

Для фотона m =0 и

Направление импульса совпадает с направлением распространения света, характеризуемым волновым вектором k, численно равным волновому числу.

Эффект Комптона.

Квантовые свойства света проявляются в эффекте, который обнаружил Комптон наблюдая рассеивание монохроматического рентгеновского излучения «легкими» веществами(графит, парафин и др.)

Опыты Комптона показали , что длина волны λ’ рассеянного излучения больше длины волны λ падающего излучения , причем разность λ’ – λ зависит только от угла рассеивания θ

λ’> λ E₁>E₂

E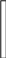 ₁=h Δ λ=

E₂=h Δ λ=

Δ λ=

λ θ

λ’

Эффектом Комптона называется упругое рассеивание коротковолнового электромагнитного излучения на свободных или слабосвязанных электронах вещества , сопровождающиеся увеличением длины волны излучения.

Вопрос №40 Корпускулярно-волновой дуализм (двойственность) света.

С увеличением частоты электромагнитных волн проявляются квантовые свойства света. Волновые свойства пренебрежимо малы. Благодаря квантовым свойствам света получило подтверждение тепловое излучение, явление фотоэффекта, эффект Контена. Присущи и волновые и квантовые свойства взаимно дополняют друг друга.

Большая частота (маленькая длина волны) - квантовые свойства.

Малая частота (большая длина волны) - волновые свойства света.

Корпускулярно-волновой дуализм вещества

Гипотеза Луи де Бройля

В 1923 году де Бройль выдвинул теорию об универсальности корпускулярно-волнового дуализма вещества. Де Бройль утверждал, что любые частицы вещества обладают волновыми свойствами наряду с корпускулярными.

Каждая частица вещества обладает:

1. Корпускулярными свойствами – импульс(P) и энергия(E).

;

;

2) Волновыми свойствами - длина волны и чаcтота

λ=; h=6,63*10^-34Дж λ=;

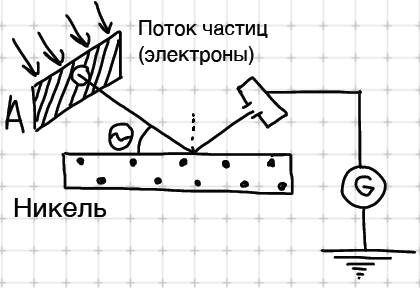
Экспериментальное подтверждение гипотезы. Был проведен опыт в 1927 году Дэвисоном и Джермером. Из утверждения, что частица - это волна, следовало то, что должна быть дифракция иинтерференция. Волны де Бройля - не электромагнитные волны, причем фазовая скорость волнде Бройля предполагалась больше скорости света, а групповая скорсть равна скорости частицы. Идея опыта Дэвисона и Джермера заключалась в том, что если микрочастицы действительно обладают волновыми свойствами, то они дрлжны отражаться от кристаллов так же, как коротковолновое электромагнитное излучение (рентгеновские лучи), то есть давать интерференционную картину в соответствие с условиями отражения рентгеновских лучей.

Релятивистскую частицу мы можем рассматривать как волну с длиной порядка 10^-10м

Волна де Бройля испытывает дисперсию, то есть их скорость зависит от длины волны частицы.

Соотношение неопределенностей Гейзенберга

Микрочастицы из-за проявления у них волновых свойств отличаются от классических частиц тем, что нельзя говорить о движении микрочастицы по определенной траектории и не правомерно говорить об одновременных точных значениях ее координат и импульса.

Микрочастицы с определенным импульсом имеет полностью неопределенные координаты, и наоборот, если микрочастице приписать точные значения координаты, то ее импульс будет полностью неопределен.

Для микрочастицы не существует состояния, в котором ее координаты и импульс имели бы одновременно точное значение, то есть соотношение неопределенностей вытекает из

волновых свойств частицы.

(так как мал); ; ;

- изменение импульса микрочастицы в результате дифракции от щели

, ,

; ;

– неопределенность Гейзенберга для импульса и координаты

Для макроскопических тел их координаты и скорость могут быть одновременно измеримы достаточно точно. Для них волновые свойства не играют роли.

Вопрос №41 Стационарное уравнение Шредингера. Частица в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Туннельный эффект.

Уравне́ние Шрёдингера — уравнение, описывающее изменение в пространстве и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах. Играет в квантовой механике такую же важную роль, как уравнение второго закона Ньютона вклассической механике. Его можно назвать уравнением движения квантовой частицы. Установлено Эрвином Шрёдингером в 1926 году.

Одномерное стационарное уравнение Шрёдингера — линейное обыкновенное дифференциальное уравнение второго порядка вида

где   — постоянная Планка,   — масса частицы,   — потенциальная энергия,   — полная энергия,   — волновая функция. Для полной постановки задачи о нахождении решения   надо задать такжеграничные условия, которые представляются в общем виде для интервала 

где   — константы. Квантовая механика рассматривает решения уравнения  , с граничными условиями   и  .

Одномерная потенциальная яма. Рассмотрим частицу, находящуюся в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. В этом случае потенциальная энергия частицы  имеет вид

     

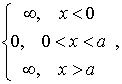
     т.е. внутри ямы ( ) потенциальная энергия  постоянна и равна нулю, а вне ямы обращается в бесконечность ( рис.4.1 ).

Запишем уравнение Шредингера для одномерного движения частицы вдоль оси 

     

Поскольку вне ямы потенциальная энергия обращается в бесконечность, то для того, чтобы выполнялось уравнение (4.11) , необходимо, чтобы вне ямы волновая функция   обращалась в ноль, т.е.  . Это означает, что в случае ямы с бесконечно высокими стенками частица не может выйти за пределы ямы, поскольку такие стенки являются непроницаемыми для частицы. В силу непрерывности волновая функция  должна обращаться в нуль и на границах ямы: при   и при  .

Таким образом, задача о движении частицы в яме сводится к решению уравнения

     

     

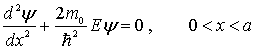
с граничными условиями

     

Введем обозначение

При этом уравнение (4.12) принимает вид хорошо известного из теории колебаний уравнения решение которого есть

Используя граничное условие  , получаем откуда следует, что  , где   . Отметим, что при четных значениях   и при   , а при нечетных значениях   . Однако, физический смысл имеет не сама волновая функция  , а квадрат ее модуля  , который от выбора значения  , т.е. от знака   не зависит. Поэтому без потери общности можно считать, что   .

Второе граничное условие   приводит к соотношению которое для   выполняется при

Отметим, что значение   , формально также входящее в решение (4.14) , не удовлетворяет условию задачи, т.к. при этом  , что означает, что частица в яме отсутствует. Поэтому значение   следует отбросить.

Подставляя (4.13) в (4.15) , приходим к выражению для полной энергии частицы, движущейся в потенциальной яме с непроницаемыми стенками   

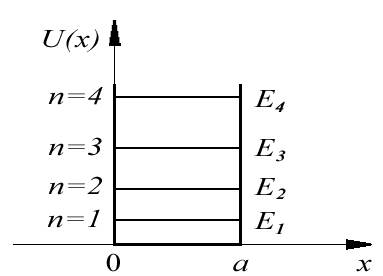
Важной особенностью полученного энергетического спектра (4.16) является его дискретность. Частица, находящаяся в потенциальной яме, может иметь только дискретные, квантованные, значения энергии, определяемые выражением (4.16) (см.рис.4.2) .

Число   в (4.16) , определяющее энергию частицы в яме, называется квантовым числом, а соответствующее ему значение   - уровнем энергии. Состояние частицы с наименьшей энергией, в данном случае с   , называется основным состоянием. Все остальные состояния являются возбужденными: значение   отвечает первому возбужденному состоянию, значение   - второму возбужденному состоянию и т.д.

Тунне́льный эффект, туннели́рование — преодоление микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелировании неизменной) меньше высоты барьера. Туннельный эффект — явление исключительно квантовой природы, невозможное и даже полностью противоречащее классической механике. Аналогом туннельного эффекта в волновой оптике может служить проникновение световой волны внутрь отражающей среды (на расстояния порядка длины световой волны) в условиях, когда, с точки зрения геометрической оптики, происходит полное внутреннее отражение. Явление туннелирования лежит в основе многих важных процессов в атомной и молекулярной физике, в физике атомного ядра, твёрдого тела и т. д.

Туннельный эффект можно объяснить соотношением неопределённостей.^[1] Записанное в виде: ,

оно показывает, что при ограничении квантовой частицы по координате, то есть увеличении её определённости по x, её импульс p становится менее определённым. Случайным образом неопределённость импульса   может добавить частице энергии для преодоления барьера. Таким образом, с некоторой вероятностью квантовая частица может проникнуть через барьер, а средняя энергия частицы останется неизменной.

Для областей   (до прохождения),   (во время прохождения внутри потенциального барьера) и   (после прохождения барьера).получаются соответственно функции:

где  ,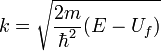 

Так как слагаемое   характеризует отраженную волну, идущую из бесконечности, которая в данном случае отсутствует, нужно положить  . Для характеристики величины туннельного эффекта вводится коэффициент прозрачности барьера, равный модулю отношения плотности потока прошедших частиц к плотности потока упавших:

Для определения потока частиц используется следующая формула:

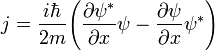
где знак * обозначает комплексное сопряжение.

Подставляя в эту формулу волновые функции, указанные выше, получим

Введем величину

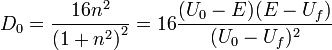
которая будет порядка единицы. Тогда:

Для потенциального барьера произвольной формы делаем замену

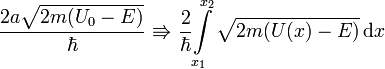
где   и   находятся из условия

Тогда для коэффициента прохождения через барьер получаем выражение

Вопрос №42 Заряд, размер, масса и состав атомного ядра. Массовое и зарядовое число ядра. Момент импульса ядра и его магнитный момент.

Ядром называется центральная часть атома, в которой сосредоточены практически вся масса атома и его положительный электрический заряд.

Заряд ядра равен величине , где e- заряд протона, Z-порядковый номер химического элемента в периодической системе Менделеева, равный числу протонов в ядре.

Состав атомного ядра.Все атомные ядра состоят из элементарных частиц- протонов и нейтронов, которые считаются двумя зарядовыми состояниями одной частицы- нуклона.Протон имеет положительный электрический заряд, равный по абсолютной величине заряду электрона.Нейтрон не имеет электрического заряда.

Масса ядра = масса атома –масса электронов

Размер атома характеризуется радиусом ядра,имеющим условный смысл ввиду размытости ядра.эмпирическая формула для радиуса:R= , где =(1,3-1,5)* м.

Зарядовое число атомного ядра — количество протонов в атомном ядре. Зарядовое число равно заряду ядра в единицах элементарного заряда и одновременно равно порядковому номеру соответствующего ядру химического элемента в таблице Менделеева. Зарядовое число обычно обозначается буквой Z. Ядра с одинаковым зарядовым числом, но различным массовым числом A (которое равно сумме числа протонов Z и числа нейтроновN) являются различными изотопами одного и того же химического элемента, поскольку именно заряд ядра определяет структуру электронной оболочки атома и, следовательно, его химические свойства.

Число нуклонов в ядре A=N+Z называется массовым числом.Массовое число у протонов и нейтронов=1, у электронов-0.

Н уклоны в атомных ядрах имеют спин h/2.Ядро атома имеет собственный момент импульса – спин ядра,равный:

=h , где I- внутреннее(полное) спиновое квантовое число.Число I принимает целочисленные или полуцелые значения(0,1/2,1..)Ядра с четными А имеют целочисленный спин,а ядра с нечетными А- полуцелый спин.

Я дерные частицы имеют собственные магнитные моменты, которыми определяется магнитный момент ядра в целом.Единицей магнитных моментов служит ядерный магнетон : = eh/(2 ), где е-абсолютное значение заряда электрона, -масса протона.Магнитные свойства атомов определяются магнитными свойствами его электронов.

М ежду спином , выраженном в h, и его магнитным моментом имеется соотношение

= , где - ядерное гиромагнитное отношение.

Магнитный момент нейтрона равен -1,91 .Знак минус показывает, что направления спина нейтрона и его магнитного моменты противоположны. Магнитный момент протона положителен и равен 2,79 .Его направление совпадает с направлением спина протона.

Вопрос №43 Дефект массы и энергия связи ядра.

Дефект массы – разность массы свободных частиц и массы ядра

Δm=[z*m_p+ (A-Z)m_n]-m_e

Масса ядра образовавшегося из свободных протонов и нейтронов меньше суммарной массы протонов и нейтронов. И эта величина определяет энергию связи.

ΔE = Δmc²[Дж] или ΔE = 935, 4 * Δm [МэВ]

Смысл энергии связи: та энергия, которая необходима для разделения ядра на нуклоны.

Свойства ядерных сил: (не поняла чем «понятие о свойствах ядерных сил» отличается от «свойств ядерных сил»)

1. Ядерные силы - это силы притяжения, так как они удерживают нуклоны внутри ядра (при очень сильном сближении нуклонов ядерные силы между ними имеют характер отталкивания).

2. Ядерные силы – это не электрические силы, так как они действуют не только между протонами, но и между не имеющими зарядов нейтронами, и не гравитационные, которые слишком малы для объяснения ядерных эффектов.

3. Область действия ядерных сил, ничтожно мала. Радиус их действия 10-13. При больших расстояниях между частицами ядерное взаимодействие не проявляется.

4. Ядерные силы (в той области, где они действуют) очень интенсивные. Их интенсивность значительно больше интенсивности электромагнитных сил, так как ядерные силы удерживают внутри ядра, одноимённо заряженные протоны, отталкивающиеся друг от друга с огромными электрическими силами.

5. Изучение степени связанности нуклонов в разных ядрах показывают, что ядерные силы обладают свойством насыщения, аналогичным валентности химических сил. В соответствии с этим свойством ядерных сил один и тот же нуклон взаимодействует не со всеми остальными нуклонами ядра. А только с несколькими соседними.

6. Важнейшим свойством ядерных сил является их зарядовая независимость, то есть тождественность трёх типов ядерного взаимодействия: между двумя протонами, между протоном и нейтроном и между двумя нейтронами.

Радиоактивность

Радиоакти́вныйраспа́д (от лат. radius «луч» и āctīvus «действенный») — спонтанное изменение состава нестабильных атомных ядер (заряда Z, массового числа A) путём испускания элементарных частиц или ядерных фрагментов. Процесс радиоактивного распада также называют радиоакти́вностью, а соответствующие элементы радиоактивными. Радиоактивными называют также вещества, содержащие радиоактивные ядра.

Установлено, что радиоактивны все химические элементы с порядковым номером, большим 82 (то есть начиная с висмута), и многие более лёгкие элементы (прометий и технеций не имеют стабильных изотопов, а у некоторых элементов, таких как индий, калий или кальций, часть природных изотопов стабильны, другие же радиоактивны).

Естественная радиоактивность — самопроизвольный распад ядер элементов, встречающихся в природе.

Искусственная радиоактивность — самопроизвольный распад ядер элементов, полученных искусственным путем через соответствующие ядерные реакции.

Энергетические спектры α-частиц и γ-квантов, излучаемых радиоактивными ядрами, прерывистые («дискретные»), а спектр β-частиц — непрерывный.

Распад, сопровождающийся испусканием альфа-частиц, назвали альфа-распадом; распад, сопровождающийся испусканием бета-частиц, был назван бета-распадом (в настоящее время известно, что существуют типы бета-распада без испускания бета-частиц, однако бета-распад всегда сопровождается испусканием нейтрино или антинейтрино). Термин «гамма-распад» применяется редко; испускание ядром гамма-квантов называют обычно изомерным переходом. Гамма-излучение часто сопровождает другие типы распада.

В настоящее время, кроме альфа-, бета- и гамма-распадов, обнаружены распады с эмиссией нейтрона, протона (а также двух протонов), кластерная радиоактивность, спонтанное деление. Электронный захват, позитронный распад (или -распад), а также двойной бета-распад (и его виды) обычно считаются различными типами бета-распада.

Некоторые изотопы могут испытывать одновременно два или более видов распада. Например, висмут-212 распадается с вероятностью 64 % в таллий-208 (посредством альфа-распада) и с вероятностью 36 % в полоний-212 (посредством бета-распада).

Образовавшееся в результате радиоактивного распада дочернее ядро иногда оказывается также радиоактивным и через некоторое время тоже распадается. Процесс радиоактивного распада будет происходить до тех пор, пока не появится стабильное, то есть нерадиоактивное ядро, а последовательность возникающих при этом нуклидов называется радиоактивным рядом. В частности, для радиоактивных рядов, начинающихся с урана-238, урана-235 и тория-232, конечными (стабильными) нуклидами являются соответственно свинец-206, свинец-207 и свинец-208.

Закон радиоактивного распада

N=N₀ e^-λt,

Где N- число оставшихся ядер

Если , то t= T_1/2 – период полураспада

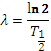- связь между периодом полураспада и постоянной полураспада.

N_{(распавшихся)}=N₀ –N₀ e^-λt=N₀(1- e^-λt)

Вопрос №44

Ядерные реакции. Реакция деления тяжелых ядер. Термоядерная реакция синтеза ядер.

Ядерная реакция – это процесс взаимодействия атомного ядра с другим ядром или элементарной частицей, сопровождающийся изменением состава и структуры ядра и выделением вторичных частиц или γ-квантов.

В результате ядерных реакций могут образовываться новые радиоактивные изотопы, которых нет на Земле в естественных условиях.

При ядерных реакциях выполняется несколько законов сохранения: импульса, энергии, момента импульса, заряда. Выполняется также ряд других законов сохранения, специфических для ядерной физики и физики элементарных частиц.

Ядерные реакции могут протекать при бомбардировке атомов быстрыми заряженными частицами (протоны, нейтроны, α-частицы, ионы). Первая реакция такого рода была осуществлена с помощью протонов большой энергии, полученных на ускорителе, в 1932 году: 

Однако наиболее интересными для практического использования являются реакции, протекающие при взаимодействии ядер с нейтронами. Так как нейтроны лишены заряда, они беспрепятственно могут проникать в атомные ядра и вызывать их превращения. Выдающийся итальянский физик Э. Ферми первым начал изучать реакции, вызываемые нейтронами. Он обнаружил, что ядерные превращения вызываются не только быстрыми, но и медленными нейтронами, движущимися с тепловыми скоростями.

Ядерные реакции сопровождаются энергетическими превращениями. Энергетическим выходом ядерной реакции называется величина 

Q = (MA + MB – MC – MD)c2 = ΔMc2.

где M_A и M_B – массы исходных продуктов, M_C и M_D – массы конечных продуктов реакции. Величина ΔM называется дефектом масс. Ядерные реакции могут протекать с выделением (Q > 0) или с поглощением энергии (Q < 0). Во втором случае первоначальная кинетическая энергия исходных продуктов должна превышать величину |Q|, которая называется порогом реакции.

Возможны два принципиально различных способа освобождения ядерной энергии.

1. Деление тяжелых ядер. В отличие от радиоактивного распада ядер, сопровождающегося испусканием α- или β-частиц, реакции деления – это процесс, при котором нестабильное ядро делится на два крупных фрагмента сравнимых масс.

В 1939 году немецкими учеными О. Ганом и Ф. Штрассманом было открыто деление ядер урана. Продолжая исследования, начатые Ферми, они установили, что при бомбардировке урана нейтронами возникают элементы средней части периодической системы – радиоактивные изотопы бария (Z = 56), криптона (Z = 36) и др.

Уран встречается в природе в виде двух изотопов:   (99,3 %) и   (0,7 %). При бомбардировке нейтронами ядра обоих изотопов могут расщепляться на два осколка.

Две типичные реакции деления этого ядра имеют вид: 

Обратите внимание, что в результате деления ядра, инициированного нейтроном, возникают новые нейтроны, способные вызвать реакции деления других ядер. Продуктами деления ядер урана-235 могут быть и другие изотопы бария, ксенона, стронция, рубидия и т. д.

Кинетическая энергия, выделяющаяся при делении одного ядра урана, огромна – порядка 200 МэВ.

Устройство, в котором поддерживается управляемая реакция деления ядер, называетсяядерным (или атомным) реактором.

Наряду с ядерным реактором, работающим на медленных нейтронах, большой практический интерес представляют реакторы, работающие без замедлителя на быстрых нейтронах. В таких реакторах ядерным горючим является обогащенная смесь, содержащая не менее 15 % изотопа   Преимущество реакторов на быстрых нейтронах состоит в том, что при их работе ядра урана-238, поглощая нейтроны, посредством двух последовательных β^–-распадов превращаются в ядра плутония, которые затем можно использовать в качестве ядерного топлива: 

2. Термоядерные реакции. Второй путь освобождения ядерной энергии связан с реакциями синтеза. При слиянии легких ядер и образовании нового ядра должно выделяться большое количество энергии. Вплоть до ядер с массовым числом около 60 удельная энергия связи нуклонов растет с увеличением A. Поэтому синтез любого ядра с A < 60 из более легких ядер должен сопровождаться выделением энергии. Общая масса продуктов реакции синтеза будет в этом случае меньше массы первоначальных частиц.

Реакции слияния легких ядер носят название термоядерных реакций, так как они могут протекать только при очень высоких температурах. Чтобы два ядра вступили в реакцию синтеза, они должны сблизится на расстояние действия ядерных сил порядка 2·10^–15 м, преодолев электрическое отталкивание их положительных зарядов. Для этого средняя кинетическая энергия теплового движения молекул должна превосходить потенциальную энергию кулоновского взаимодействия. Расчет необходимой для этого температуры T приводит к величине порядка 10⁸–10⁹ К. Это чрезвычайно высокая температура. При такой температуре вещество находится в полностью ионизированном состоянии, которое называется плазмой.

Энергия, которая выделяется при термоядерных реакциях, в расчете на один нуклон в несколько раз превышает удельную энергию, выделяющуюся в цепных реакциях деления ядер. Так, например, в реакции слияния ядер дейтерия и трития 

выделяется 3,5 МэВ/нуклон. В целом в этой реакции выделяется 17,6 МэВ. Это одна из наиболее перспективных термоядерных реакций.