Глубокие примесные центры.
Из условия E~Eg можно определить радиус связи состояния
15-2
=>
Масштабы локализации: реализуется на масштабе элементарной ячейки. Свойства примесных центров чувствительны к дефектам.
Свойства глубоких уровней.
Амфотерность – любая примесь может быть и донором и акцептором.
Многозарядность – один и тот же примесный атом может создавать несколько различных уровней с различающимся зарядом.
Как образуются связанные состояния на отталкивающем потенциале?
П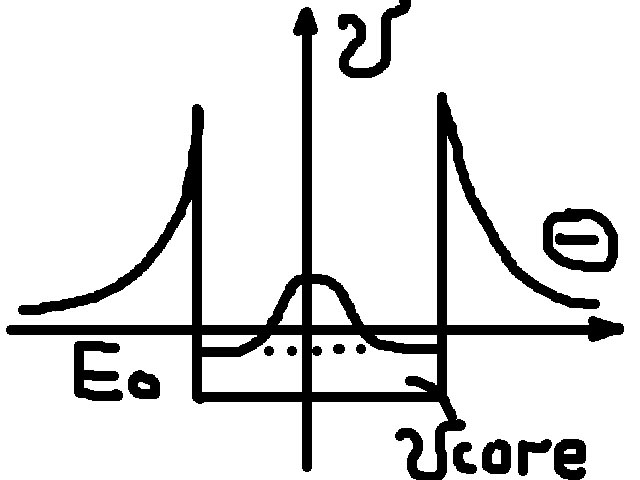
усть
на большом расстоянии от этого центра
имеется кулоновский потенциал, но вблизи
центра может существовать потенциал,
отличный от кулоновского, и даже имеющий
вид потенциальной ямы.
->Возникает перестройка решетки, потенциальная энергия понижается, становится выгоден переход на этот центр.
->Образование химической связи – Дополнительные носителинасышают ненасыщенные валентные связи.
С точки зрения зонной теории глубокие центры отличаются тот мелких тем, что их волновая функция сформирована из блоховских функций, принадлежащих различным зонам.
(зона проводимости),
(валентная
зона).
Г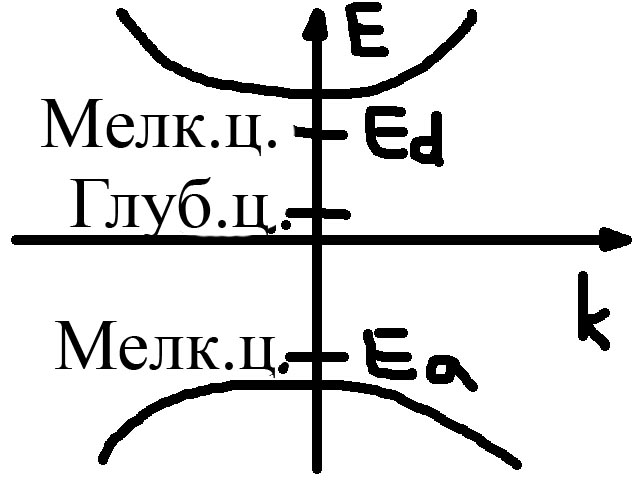
лубокие
центры:
m*>0 m*<0
Методы описания
Метод эффективной массы вследствие r0~a(переменной решетки), не применим(волновая функция плавно меняется на периоде решетки!). Для наглядного описания модно пользоваться методом сильной связи, а для количественного необходимо проводить численные расчеты.
Поляризация тела
есть сумма поляризаций всех физических
подсистем.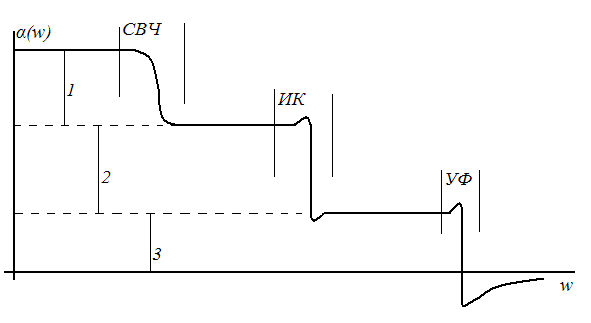
,
,
При низкой w все 3 физические подсистемы успевают за изменением внешнего поля.
При увеличении «выключается» дипольная поляризация (интервал СВЧ излучения), за тем ионная (интервал ИК излучения). При очень высоких частотах «выключается» и электронная поляризация.
29-2
31. Оптические свойства диэлектриков.
31-1
,
где
- диэлектрическая проницаемость с учетом
динамической поляризации
.
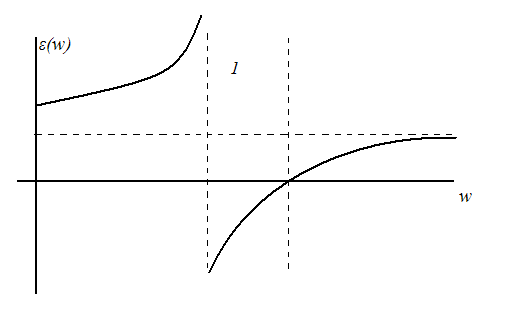1
- полоса
непрозрачности.
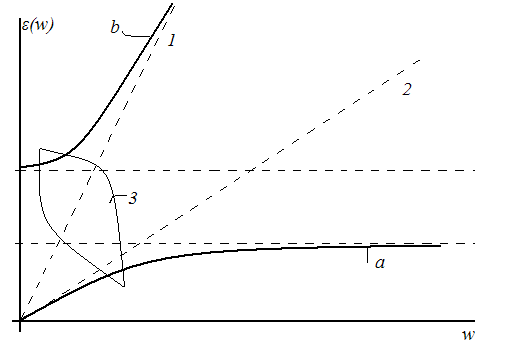
1
-
,
2
-
,
a
– поперечный
фонон, b
– продольный фонон.
3 – связанные фонон-фононные колебания. При квантовом описании им соответствуют свои новые частицы – поляритоны.
В объемных кристаллах колебания кристалла – это фононы. Для образования поляритона частота э/м поля находиться в области собственных резонансов кристалла (частота резонанса должна быть достаточно мала).
Существуют другие типы резонансов с образованием аксетонов (связанное состояние электрон-дырка).
32-1
Сегнетоэлектрик
– вещество, в котором при некоторой
(Крит.)
возникает спонтанная поляризация. (
при внешнем поле
)
;
;
При Е=0
;
система не устойчива.
Типы сегнетоэлектриков :
1) Упорядочения –
кристаллы с водородными связями; Водород
легко отдаёт свой электрон, что приводит
к возникновению поляризации. Малый
радиус
легко меняется направление дипольного
момента:
P=0;
P
0;
Замена водорода
на дейтерий повышает
в 2 раза, увеличивается радиус.
2) Смещения – ионный
кристалл. Ионы взаимодействуют друг с
другом. Возникает флуктуация
внутренне
поле
поляризация
(обратная связь, неустойчивость системы)
;
;
;
=2930К;
Микроскопические механизмы сегнетоэлектрического перехода. 1)Поляризационная «катастрофа»
;
Если поляризуемость возрастает
;
Нарастание диэлектрической проницаемости.
Локальное электрическое поле, обусловленное поляризацией, возрастает быстрее, чем упругие тормозящие силы, действующие на ионы в кристалле. Что приводит к ассиметричным смещениям ионов из положения равновесия. Для все положительные ионы смещены вверх (Ва, Ti), все отрицательные смещены в низ (O)
2) Из соотношения
Видемана-Франца
;
=
эквивалентно, что
=0;
Ситуация, когда имеет место понижение некоторой собственно частоты, называется смягчением соответствующей моды колебаний. В данном случае при переходе в сегнетоэлектрическое состояние, происходит смягчение поперечной оптической моды колебаний в системе.
В ФТТ существуют различные исследования влияния взаимодействия на частоты. Такой механизм называется мягкой модой.
Пироэлектрики
Пироэлектрики – вещества, у которых существует поляризация при любой температуре, вплоть до температуры плавления. Иначе это сегнетоэлектрик, у которого Тс находится выше Тплавл . Наличие поляризации означает отсутсвие инвариантности системы относительно инверсии координат. Т.е. пироэлектриком могут быть только не центросимметричные вещества, группа симметрии которых не содержит центра инверсии и допускает существование полярной оси.
33-1
Описание строиться на основе общей теории Ландау фазовых переходов.
Фазовые переходы:
I рода: свойства системы меняются скачком.
II
рода: свойства системы меняются
непрерывно. Для описания переходов II
рода Ландау предложил подход, основанный
на разложении энергии вблизи Т перехода
в ряд по степеням параметра порядка.
Параметр порядка – физическая величина,
которая характеризует изменения свойств
системы при фазовом переходе. Как правило
фазовый переход сопровождается изменением
симметрии системы. Поэтому, часто
параметром порядка называют физическую
величину, которая несёт информацию об
изменении симметрии системы. Примеры
параметра порядка:
;
- переход в магнитное состояние
;
-
магнитный момент;
- антиферромагитный вектор;
-
функция, тоже параметр перехода.
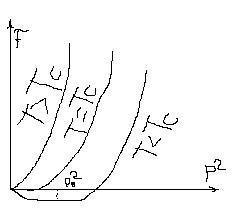
Закон
Кюри-Вейсса (обращение
в
)
Разложения
Ландау:
;
F-
плотность свободной энергии.
-
член взаимодействия с полем.
;
;
- макроскопические
хар-ки
E
=0;
Условие min
свободной энергии:
;
;
-равновесное
условие.
;
существует только для
,
оно и есть решение для min
свободной энергии.
С изменением температуры возникает новое физическое свойство.
, найдём ;
-
индуцир.внеш.полем;
-
спонтанная;
Условие
min
энергии
;
;
;
;
34-1
С
макроскопической точки зрения магнитные
свойства вещества описываются магнитной
проницаемостью µ ,
-
индукция
магнитного поля.
,
Намагниченность - плотность магнит. момента вещества
Вещества в которых
при
называются ферромагнетиками
Пусть при
,
, тогда
где
-
магнитная восприимчивость, то
По
определению при T=0
при
F=E-TS
F-свободная
энергия.
Тогда при
- парамагнетики.
При
- диамагнетики.
Причиной возникновения магнитного момента может служить ориентация спинов или(и) орбитальное движение носителей заряда ( микроскопические электрические токи).
И токи, и спины могут быть связанны как с электронами атомных остовов , так и с валентными делокализованными электронами.
Если магнитный момент определён электронами атомных остовов, то магнетики с локализованными моментами.
Если наш момент определяет делокализованный электрон, то такие магнетики называются несобственными.
Парамагнетизм локализованных моментов - парамагнетизм Кюри.
Парамагнетизм делокализованных моментов - парамагнетизм Паули.
Диамагнетизм локализованных моментов - диамагнетизм Ланжевена.
Диамагнетизм делокализованных моментов - диамагнетизм Ландау.
Классификация магнетиков по пространственному распределению:
Ферромагнетики
( все моменты в одну сторону)
Антиферромагнетики
,
но
(
имеются минимум 2 подрешётки и моменты
этих решёток равны и противоположны)
Ферримагнетики
34-2
Диамагнетизм локальных моментов- диамагнетизм Ланжевена
Диамагнетизм делокализованных моментов - диамагнетизм Ландау
На микроскопическом уровне взаим. вещ-ва с магнит. полем связанно с движением заряженных частиц и их спином. При этом если отношение орбитального магнитного момента к механ. орбитальному моменту есть -e/2mc , то для спинового (-e/2mc)*g0 , g0≈2
Магнитное поле в гамильтониан можно ввести 2 способами :
в орбитальную компаненту
;
(импульс удлиняется),
(*)в спиновую степень свободы ∆
=
g0μBHSz
,
rot
=
;
div
=0;
Удобно выбрать калибровку
подставим в (*)
,
где
-гамильтониан
( писать как H
)
Далее применяем
теорию возмущения. При этом для n-го
уровня возникает следующий
|n>-собственные волновые функция n-го уравнения в отсутствии возмущения
Возникает 3 члена
Пусть имеем дело с полностью заполненной оболочкой. В атомах заполнение электронных оболочек происходит по правилу Хунта. n-главное квантовое число
l-орбитальное квантовое число ,m –магнитное квантовое числа, s –спин. J- полный момент.
где J
: ...L+S
... |L-S|
В случае полной
замкнутой оболочки
это означает что,
в ∆E
остаётся только 3 последний член
,
F-свободная
энергия