13. Контакты металл – полупроводник.

13-2

Контакт Шоттки: вольт – амперная характеристика.

- работа выхода из металла.

У ровни Ферми должны выровняться. Можно рассмотреть контакт Ме-п/п, можно рассмотреть переход, где концентрация электронов в одном из них очень велика.

Поле в Ме экранируется на масштабе порядка межатомного.

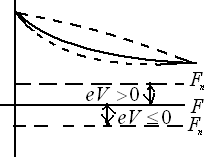
В результате контакта на границе Ме-п/п возникает барьер для электронов.

Существует 2 теории для анализа контакта Шоттки (отличаются механизмом, ограничивающим токоперенос через контакт):

Диодная – ток ограничен.

Диффузионная – ток ограничен диффузионными процессами в объёме п/п.

ВАХ контакта Шоттки.

Положительное смещение соответствует минусу на Ме и плюсу на п/п n типа (зоны смещаются вверх). При положительном барьер уменьшается, при отрицательном сужается (возрастает).

– величина барьера со стороны п/п.

– барьер со стороны Ме (не измен.)

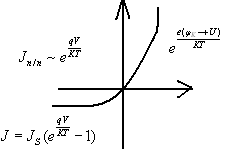
В состоянии равновесия токи уравновешены:

при V=0:

при V<0: , т.е. доля электронов, способных преодолеть барьер уменьшается.

при V>0:

- из Ме в п/п, ток термоэлектр. эмиссии (способен преодолеть фиксир. барьер);

;

n - эффективная плотность состояния

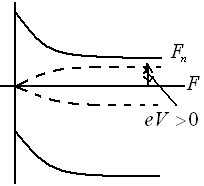
Распределение квазиуровней Ферми.

В диодной теории:	В диффузионной теории:
Скачком меняется квазиуровень Ферми.

5-2

-общий вид решения. А и B опред. из гран. усл.

На бескон. поле обращ. в ноль => B=0,

А определяется из гран усл. в нуле

, L_Д-это расст., на котором поле в невырожденном п/п уменьшается в e раз.

Неоднородный электрост. потенц. приводит к неодн. распред. носителей заряда. Качественно эту картину можно описать на языке краевых зон.

,

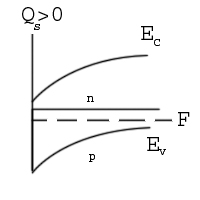
Пусть Q_S>0, найти зоны внутри п/п. Если Q_S>0, то потенц. >0 => энергия понижается. В сост. равн. (отсутствие тока) полож. ур. Ферми постоянно, его положение фиксир. объемом.

Когда протекает эл. ток, то исп. понятие квазиуровня Ферми.

Для n-типа такой изгиб зон — обогащение носителей, для p-типа – обеднение.

Если p-типа и изгиб зон очень сильный, тогда осн. носит. заряда изменяются, т.е. инверсия типа проводимости (в приповерхностных обл.)

З оны искривл. вверх. Для p-типа обогащ., для n-типа- обеднение. Если зоны искривл. сильно, то возможна инверсия типа проводника.

При сильном пов. потенц. край зоны вблизи поверх. может пересеч ур. Ф., т.е. возникнет вырождение. Вблизи пов-ти образ двумерн. электр. газ (2D – эл. газ.)

Прикладыв. к пов-ти заряд того или иного знака, можем менять концентр. носит. заряда => и проводимость в приповерх. слоях. Это и есть эффект поля, кот. заключ. в изменении пров-ти припов. слоя под действием внеш. поля. Этот эффект и лежит в основе действия полевого транзистора.

12-2

На прямой ветви преобладает рекомбинационное слагаемое:

– учет рекомбинационных токов; n – фактор неидеальности (1<n<2);

5 участок: вклад последовательных сопротивлений, уменьшающих эффективное напряжение на переходе.

18-1

18. Гармонические колебания кристаллической решётки и нормальные моды колебаний решётки.

Степени свободы кристалла – это количество переменных которые необходимы, чтобы описать колебания кристалла.

эл. ячеек в кристалле, в каждой ячейке атомов, каждый атом может смещаться в трёх направлениях ( ).

- степеней свободы (полное число).

Дальнейший вывод уравнений колебания кристаллов аналогичен выводу уравнения колебаний грузика на пружине . Основное отличие – большее число степеней свободы.

В формализме Лагранжа: ; ; ;

; – это гармоническое приближение.

Смещение S-ого атома в R-й элементарной ячейке в J-ом направлении: ,

Вектор обозначает разные элементарные ячейки.

Всего таких параметров .

– кинетическая энергия

– потенциальная энергия.

Ограничимся только квадратичными членами, получим гармоническое приближение.

Слагаемые порядка больше 2 – ангармонические, получим ангармоническое приближение.

Введём силовой тензор:

- уравнение движения

Записанное соотношение представляет собой систему из ур. (нерешаемая задача)

С учётом теоремы Блоха будем искать решение в виде

– силовой тензор зависит от расстояния между ячейками (Сила действующая со стороны на в ячейках и соответственно)

19-1

19. Квантование колебаний решетки. Фононы. Экспериментальные методы исследования спектра фононов.

Любые колебания крист. можно представить в виде совокупности норм. мод. С другой стороны, согласно общим принципам квантовой механики, любые колебания можно представить в виде совокупности квантов колебаний. При этом Q – обощенная координата.

– лагранжево описание на языке обобщенных скорости и координаты

Существует другое описание (гамильт.):

– обобщенный импульс

на языке операторов в квантовой механике

применим эту схему для описания колебаний решетки:

сумма гамильтонианов гармонического осцил.

– это ур-ние Шредингера для гарм. осцилл., соотв. норм. моде P.

– квант. энергия гарм. осцилл.

n – число квантов колебаний данного типа,

Фонон – квант колебаний кристаллической решетки. Т.о. различные классич. норм. моды колебаний кристалла на квантовом языке превращаются в различные фононы. Число типов фононов равно числу типов норм. колебаний. А число фононов данного типа опред. амплитуда колебаний нормальной моды – рожд. новые фононы.

(*)

– число фононов данной моды с заданной длиной волны.

Фонон – квазичастица (способ представления сложной системы в виде набора невзаимодействующих квазичастиц). Фононы не взаимодействуют в гармоническом приближении. Спина нет, заряда – нет.

Бозон – ф-ция распределения Бозе-Эйнштейна:

Число фононов не постоянно, они появляются и исчезают (колеб. системы). Число фононов определяется минимумом термодинамического потенциала . Условие минимума совпадает с определением