6.3.2. Задача компоновки модулей нижних уровней.

С учетом перечисленных особенностей появляется возможность выделить и проанализировать основные задачи конструкторского синтеза РЭС. Проделаем это на примере проектирования пространственного (компоновочного) решения ячейки.

ПРИМЕР: Ячейка, рис. 6.7., состоит из некоторого числа N микроэлектронных узлов (МЭУ), расположенных на печатной плате (ПП).

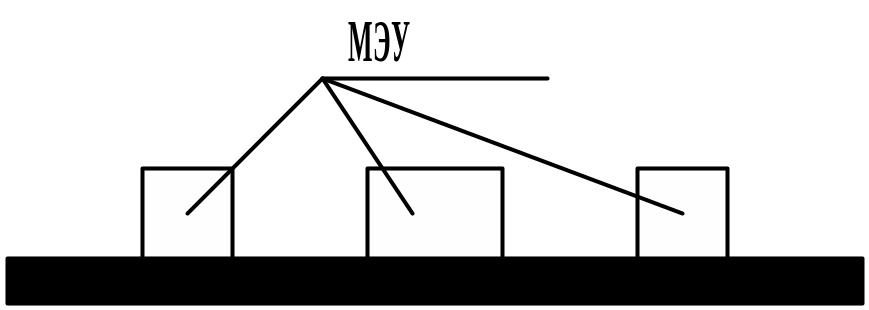
Рис. 6.7. Ячейка (субблок) РЭС.

Следовательно, необходимо синтезировать пространственную систему S_пр, состоящую из N+1 элементов Г = {₁, ₂, … _N, _N+1} c априорно известной структурой Θ_пр = { Θ ₁, Θ₂, … Θ_m } всех видов отношений R₁, R₂, … R_m . Рассмотрим совокупность R_пр = { R₁, R₂, … R_m} пространственных отношений между элементами Г, которые существуют в данной системе и которые необходимо определить.

Начнем с синтеза унарных отношений R₁. Указанные отношения описывают пространственные свойства элементов, в нашем случае - МЭУ и ПП.

Пространственная структура Θ ₁ унарных отношений R₁ означает не что иное, как форму всех N+1 элементов. В данном случае - это плоские прямоугольные элементы (высотой МЭУ можно пренебречь). Поскольку форма известна, значит известны структуры Θ₁ унарных пространственных отношений R₁.

Конституэнты Е₁ отношений R₁ представляют собой пространственные параметры элементов, а именно, их геометрические размеры, т.е.

Е₁ = {Х₁, Х₂, … Х_N, Х_N+1},

где Х_i - множество параметров (геометрические характеристики) МЭУ и ПП, X_i = {x_1i, x_2i}; x_1i, x_2i - длина и ширина i- го МЭУ.

Совокупность бинарных отношений R₂ описывает пространственное отношение пар элементов хГ², хГ² = ГхГ.

Структура Θ₂ бинарного пространственного отношения R₂ задается рисунком или вербально (словесно): "все МЭУ располагаются строго ориентировано на одной стороне ПП не наползая друг на друга". Знание структуры Θ₂ позволяет сделать вывод, что из множества отношений R₂ пар элементов хГ² наиболее существенны отношения R'₂, R'₂  R₂, описывающие свойства множества пар МЭУ-ПП. Указанное свойство определяет пространственное положение каждого МЭУ на ПП. При этом из множества пар хГ² выделяется с помощью R'₂ некоторое подмножество Г_s'  хГ² , а именно

Г_s' = {<₁, _N+1>,< ₂, _N+1 >, … < _n, _N+1>}.

Рассматривая отдельно каждую пару <_i, _N+1> элементов из множества хГ² можно установить, что в качестве конституэнт бинарных отношений выступают два параметра - координаты положения на плоскости одного элемента относительно другого. Отсюда следует, что в качестве конституэнт Е₂ отношений R₂ в общем случае выступает оператор ψ размещения МЭУ на поверхности ПП или координаты положение МЭУ на ПП

Е₂ = ψ .

Из множества многоместных отношений выделим (N+1) - арное отношение R_N+1, а именно то, которое описывает отношение пространственного соответствия всех N узлов и ПП, т.е. для Г_S"  хГ^N+1,

Г_s'' = {<₁, ₂, … _N, _N+1>}.

По смыслу это пространственное отношение выражает свойство соответствия площади Р_мэу , занимаемой множеством МЭУ и площадью Р_пп ПП, R'_N+1: .

Конституэнта Е_N+1 отношения R_N+1 в простейшем случае (при одинаковых размерах всех МЭУ) представляет собой константу N_max, Е_N+1=N_max.

где N_max - максимальное количество МЭУ, располагаемое на ПП, N ≤ N_max. В общем случае конституэнта Е_N+1 представляет собой алгоритм g распределения (выделение списка, компоновки) МЭУ для установки на конкретной ПП,

Е_N+1 = g.

Следует учесть, что совокупность свойств Х_N+1 ПП должна включать в себя свойства, определяющие рисунок (топологию) электрических связей. В общем случае, кроме обычных размерных параметров Х'_N+1, включается в Х_N+1 и оператор прорисовки (трассировки) связей π (по аналогии с операторами компоновки и размещения),

Х_N+1 = {Х'_N+1, π }.

Таким образом, для синтеза указанной пространственной системы S_пр необходимо определить следующую совокупность конституэнт отношений

Е_пр = {Х₁, Х₂, … Х_i, … X_N, g, {X'_N+1, π }, ψ }

В нашем примере совокупность Х₁, Х₂, …, X_N известна.

Очевидно, что подобные по содержанию задачи приходится решать и при синтезе конструкции модулей и других иерархических уровней.

Из приведенного примера видно, что конструктор должен решать следующие задачи в процессе синтеза современной РЭС:

• выбор совокупности конструктивных модулей всех иерархических уровней с определением их типоразмеров (определение Х или Х_N+1);

- определение списка модулей всех уровней (определение g или N);

- размещение модулей (определение ψ);

- трассировка электрических связей между модулями (определение π).

Интересно, что рассматривая проектирование S_пр с общих позиций, удалось установить только перечень задач синтеза, которые необходимо решить, но ничего не известно о последовательности решения.

Простейший анализ показывает, что синтез конституэнт Е_пр должен бы быть выполнен одновременно, но сейчас это невозможно. В инженерной практике проектирования конструкций РЭС используют, как уже было сказано, последовательную схему работ.

Рис. 6.8. Последовательность задач компоновки.

Перейдем теперь к рассмотрению типовых задач анализа полученного пространственного (компоновочного) решения РЭС. Далее в курсе этот вопрос будет рассматриваться подробнее, сейчас же только укажем без объяснения перечень таких задач. К ним относятся:

• анализ теплового режима;

• анализ устойчивости к механическим воздействиям;

• анализ электромагнитной совместимости элементов;

• анализ надежности РЭС;

• анализ затрат на жизнь РЭС и т.д.

Т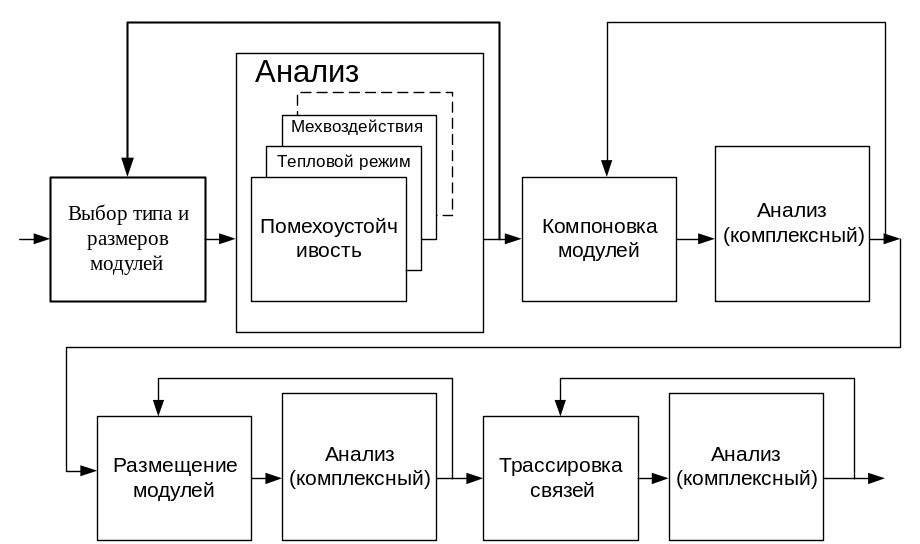 аким образом, можно представить себе содержательную модель конструирования РЭС (перечень задач) в следующем виде, рис. 6.9.

Рис. 6.9. Содержательная модель конструирования.

Следует отметить, что не всегда анализ после каждого этапа осуществляется в полном объеме; и, второе, схема работ (задач) не имеет в своем составе задач принятия решения, хотя реально они присутствуют на каждом этапе и являются чрезвычайно важными с точки зрения качества полученного окончательного решения.

6.4. Унифицированные конструкции модулей первого уровня.

Унифицированные конструктивные решения модулей 1-го уровня выполняются практически по двум вариантам: корпусированный и бескорпусный модуль.

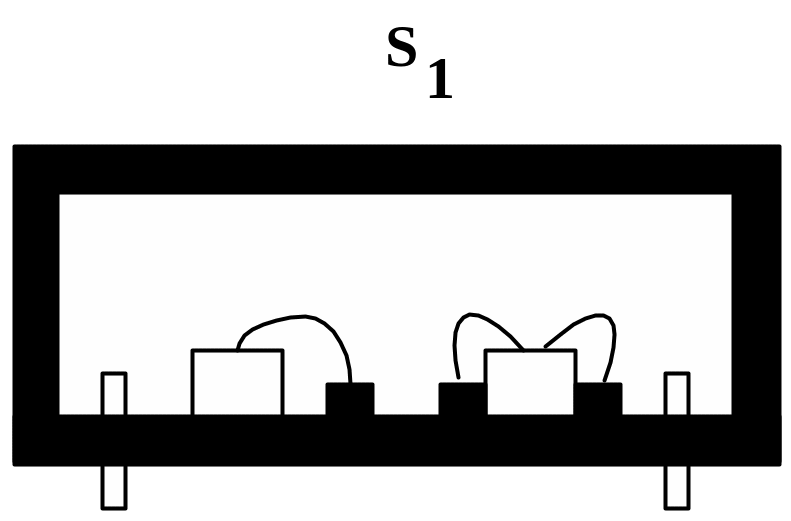
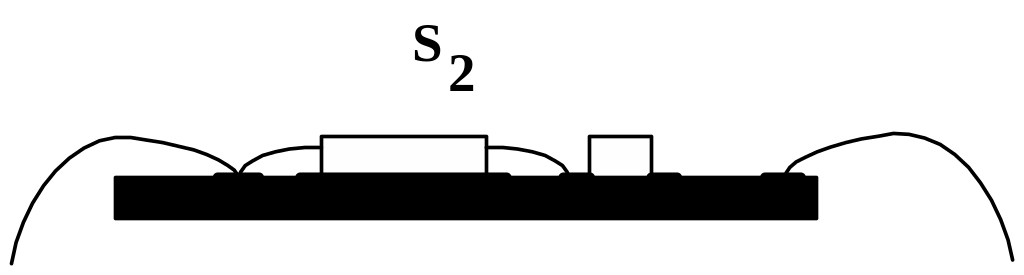
Рис. 6.10.Унифицированные конструкции.

В целом оба варианта характеризуются тем, что заранее известен принцип П компоновки, набор основных элементов Г, компоновочная схема Θ и задан ряд типоразмеров будущей конструкции модуля.

6.4.1. Корпусированные микросхемы и микросборки.

Корпус является конструкторской базой, на которой устанавливаются микроплаты и навесные компоненты МКС. Корпуса выполняют ряд функций:

• защиту от механических и климатических воздействий;

• экранировку от помех;

• упрощение сборки МКС;

• унификацию исходного конструктивного элемента по габаритам и установочным размерам.

Корпуса бывают:

• металлостеклянные (сварка крышки с основанием). Обеспечивают надежность, высокую плотность монтажа, минимизацию габаритов, но дороги;

• металлокерамические (пайка, сварка), применяются пока в 4 типе корпусов;

• металлополимерные (заливка). Технологичны, дешевы, отсутствие нежелательных воздействий при герметизации, но малая допустимая мощность рассеивания (до 100мВт);

• керамические (окись алюминия, пайка), не получили пока широкого распространения;

• пластмассовые (стеклоэпоксидные, опрессовка). Дешевы, но возможен перегрев.

По конструктивным разновидностям и габаритным размерам корпуса отечественных МКС унифицированны. В ГОСТе 17467-79 (микросхемы интегральные. Корпуса. Типы и размеры) установлены 5 типов корпусов по таким признакам, как проекция тела корпуса на плоскость основания и расположению выводов.

По габаритным и присоединительным размерам типы корпусов подразделяются на подтипы и типоразмеры, каждому из которых присваивается шифр, состоящий из слова «Корпус», обозначения типоразмера корпуса и порядкового номера типоразмера (двузначное число от 1 до 99).

В конструкторской документации корпусам присваивается еще и цифра, обозначающая число выводов МКС, и порядковый номер разработки.