2. Метод параллельного сближения.

Является одним из основных методов самонаведения.

При использовании этого метода линия ракета-цель перемещается параллельно самой себе.

=0 ( =0, =0)

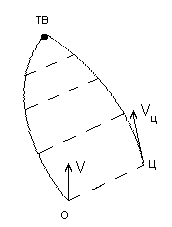
Этот метод в отношении нормальных и потребных перегрузок обладает оптимальным свойством: потребные перегрузки меньше, чем при наведении любым другим методом.

Потребные перегрузки не превосходят перегрузки, с которыми маневрирует цель. Если цель не маневрирует, то потребные перегрузки равны 0.

С инета:

При данном методе вектор скорости ракеты V_p в каждый момент времени t направлен в точку упреждения, то есть точку, где произошла бы встреча цели и ракеты, если после момента времени t они двигались бы равномерно и прямолинейно . Рассмотрим ситуацию, представленную на рисунке:

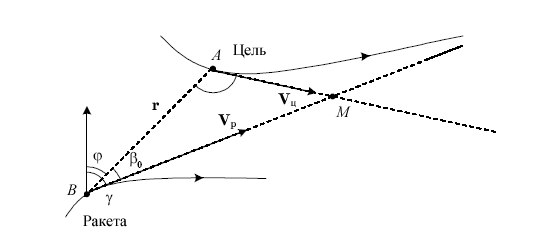
Здесь цель и ракета движутся по некоторым криволинейным траекториям и в момент времени t находятся, соответственно, в точках А и В. Точка упреждения М для момента времени t находиться как точка пересечения лучей, являющихся продолжением векторов скоростей цели V_ц и ракеты V_р. Угол β_о можно определить из треугольника АВМ.

Угол β_о называется идеальным углом упреждения. В любой момент времени угол упреждения для метода параллельного сближения должен быть равен β_о.

При движении цели угол α, угол между вектором скорости цели V_ц и направлением на ракету, постоянно меняется. Следовательно, будет меняться и угол β_о. Однако, как показывает анализ, вектор r, соединяющий точки расположения ракеты и цели, будет перемещаться в пространстве параллельно самому себе, не вращаясь. Это свойство определило название метода. Учитывая последнее обстоятельство, для метода параллельного сближения будет справедливо равенство:

По сравнению с методом погони метод параллельного сближения дает минимальную кривизну траектории движения ракеты.

Билет №3

1 Упрощенный метод оценки параметров автоколебаний в контурах угловой стабилизации.

В нелинейной автоколебательной САУ эффективный коэффициент усиления регулятора по медленной составляющей сигнала обратно пропорционален амплитуде автоколебаний, которая, в свою очередь, является некоторой функцией переменных параметров объекта управления. Причем если амплитуда автоколебаний при некоторых структурах САУ прямо пропорциональна коэффициенту усиления объекта, зависимость ее от других параметров объекта более сложна.

САУ технически работоспособна при амплитуде автоколебаний, не превышающей некоторое максимальное значение, поэтому пределы изменения переменных параметров объекта управления, при которых САУ сохраняет свою работоспособность, жестко ограничены. Их можно значительно расширить путем выбора рациональной структуры САУ.

Анализ и синтез таких систем удобно проводить на базе метода гармонической линеаризации.

Известно, при выполнении условия

где - внешнее воздействие; Т – период автоколебаний нелинейной САУ, процессы в некоторой нелинейной системе приближенно можно описать следующими уравнениями:

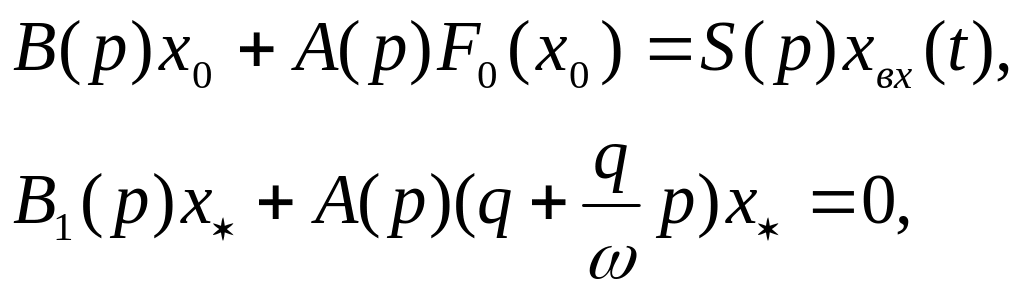
где - функция смещения соответствующего для медленного меняющейся составляющей; - медленно меняющаяся составляющая; - высокочастотная колебательная составляющая.

Учитывая, что , как правило, является непрерывной плавной функцией, при малых значениях ее можно линеаризовать, т.е.

Тогда уравнение для медленного меняющейся составляющей можно записать в виде где - эквивалентный коэффициент усиления нелинейного усилителя, т.е. по отношению к медленно меняющимся внешним воздействиям такая система ведет себя как линейная.

В связи с этим при медленно меняющихся воздействиях автоколебательную САУ можно заменить эквивалентной линейной.

Для пояснения:

Физическая картина работы системы угловой стабилизации на упругой ракете

Пусть программное положение x₁ следующее:

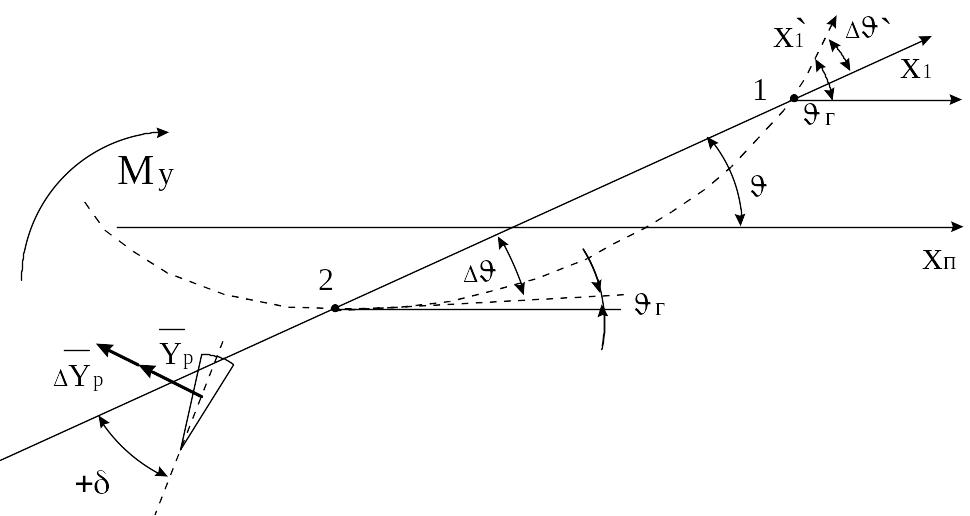
Но под действием возмущений продольная ось отклонилась от программного направления. Пусть гироприборы расположены в точке 1, тогда

.

 будет измерена гирогоризонтом и произойдёт отклонение руля на угол На руль действует подъёмная сила Y_p, создающая момент M_y, возвращающий КА к x_п. Но под действием Y_p происходит прогиб. Если гироприборы находятся в точке 1, то они реагируют уже на _г= + ’.

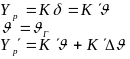
Возникнет увеличение подъёмной силы на руле.

Таким образом, при расположении гироприборов в носовой части ЛА через систему угловой стабилизации по упругим колебаниям реализуется положительная обратная связь. Она приводит к нарастанию амплитуды упругих колебаний. Амплитуда будет возрастать, пока в каком-то звене не сработает насыщение или ограничение. Тогда прекратится рост амплитуды и появятся автоколебания на частотах упругих автоколебаний.

Если гироприборы будут находиться в точке 2, то знаки в уравнениях для угла поворота руля и подъёмной силы руля поменяются на противоположные, и с точки зрения возврата x₁ к x_п добавка к подъёмной силе руля будет играть негативную роль, но с точки зрения прогиба эта добавка способствует разгибанию ЛА. При расположении гироприборов в хвостовой части ЛА по упругим колебаниям через систему угловой стабилизации реализуется жёсткая обратная связь. Упругие колебания будут затухать, поэтому гироприборы необходимо ставить в хвостовой части. Но по первому тону в точке 2 действительно существует устойчивый тон упругих колебаний, в то время как в точке 1 неустойчивый, зато по другим тонам мы можем получить картину обратную. Кроме того, нам придётся иметь гироприборы на каждой ступени ракеты или потребуется их лифтирование. Это в ряде случаев неприемлемо, поэтому, как правило, гироприборы устанавливают в носовой части, но приходится принимать меры по подавлению упругих колебаний. Можно ставить фильтры подавления упругих колебаний. Обычно это узкополосные самонастраивающиеся фильтры, тогда мы разрываем обратную связь по упругим колебаниям, и они затухают сами по себе за счёт диссипативных сил (потеря энергии в конструкции). Если колебания гаснут за счёт диссипативных сил, то такой способ называется пассивным. Активным называют способ, когда в гашении колебаний участвуют рули.

Если в диапазоне частот упругих колебаний инвертировать знак тогда и добавка Y тоже получится с минусом. Инвертирование знака у равносильно переносу гироприборов из точки 1 в точку 2. Другой способ реализуется на основе сдвига фаз

Это фазовое подавление упругих колебаний (здесь уже участвуют рули).

Сложность в том, что должен иметь место большой излом в фазочастотной характеристике корректирующего звена.