§6. Соприкасающийся параболоид к поверхности.

О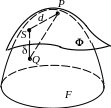 пределение. Пусть две поверх-ности  и F имеют общую точку P и общую касательную плоскость  в этой точке. Пусть S – близкая к P точка. Проведем через S прямую, перпендикулярную плоскости . Она пересечет F в некоторой точке Q . Обозначим d = | PS | , =|QS | . Говорят, что поверхности  и F соприкасаются в точке P, если Combin = 0.

Теорема 3. Пусть  – регулярная поверхность класса C². Тогда в каждой ее точке существует, и притом единственный, соприкасающийся параболоид, который может вырождаться в параболический цилиндр или плоскость.

Доказательство. Пусть P – произвольная точка, а  – касательная плоскость к  в точке P. Введем в пространстве декартову СК Oxyz так, чтобы P = O, а  совпадала с Oxy. Тогда поверхность  в окрестности точки P можно задать уравнением в явном виде

z = f(x, y).

При этом, (0, 0) = 0. В соответствии с (7) уравнение касательной плоскости в точке P имеет вид

z = x · f_x(0, 0) + y · f_y(0, 0).

Но в нашей СК касательная плоскость имеет уравнение z = 0. Значит,

f_x(0, 0) = f_y(0, 0) = 0. ()

Поэтому разложение функции f(x, y) в ряд Тейлора в окрестности точки (0, 0) имеет вид:

f(x, y) = (f_xxx² + 2f_xyxy + f_yyy²) + (x, y)(x² + y²),

где (x, y) ^– 0 при x, y ^– 0. Значит, уравнение поверхности  в окрестности точки P имеет вид

z = (f_xxx² + 2f_xyxy + f_yyy²) + (x, y)(x² + y²).

(все производные вычисляются в точке (0, 0)). Определим поверхность F уравнением

z = (f_xxx² + 2f_xyxy + f_yyy²). ()

Пусть S(x, y, z) – близкая к P точка. Тогда точка QF имеет те же координаты x, y, что и точка S, т.е. Q(x, y, z) 

 = z – z= (x, y)(x² + y²) , d = | OS | = ;

= ^– 0

при x, y ^– 0, т.к. 0   1.

Выясним, какого типа поверхность F определяется уравнением (). С учетом (), формулы (13) дают L = f_xx, M = f_xy , N = f_yy . Значит,

уравнение F имеет вид

2z = L x ² + 2M xy + N y² . (22)

Если мы, к тому же, направим координатные оси Ox и Oy по главным направлениям поверхности  в точке P, то уравнение F примет вид

2z = ₁x² +₂ y² .

Теперь очевидно, что для эллиптической точки P поверхность F будет эллиптическим параболоидом, для гиперболической – гиперболическим параболоидом; для параболической точки P уравнение F примет вид

2z = ₁x² или 2z = ₂ y^2,

^{а значит} F будет параболическим цилиндром. В точке уплощения имеем уравнение 2z = 0  F будет плоскостью.

Е динственность соприкасающегося параболоида примем без доказательства.

Мы выяснили, что

1) ближайшая окрестность эллиптической точки P похожа на окрестность вершины эллиптического параболоида;

2 ) ближайшая окрестность гиперболической точки имеет седлообразную форму, как область на гиперболическом параболоиде.

3) ближайшая окрестность параболической точки похожа на область на параболическом цилиндре.

4 ) ближайшая окрестность точки уплощения мало отличается от плоской области, но более точное изучение может показать, что эта окрестность имеет очень сложную структуру.

Пусть F – соприкасающийся

параболоид к поверхности  в точке P . Пусть декартова СК в пространстве выбрана также, как и в доказательстве теоремы и (22) – уравнение F. Рассмотрим сечение F плоскостью z = 1/2 . Получившуюся кривую спроецируем в касательную плоскость. Тогда уравнение проекции  будет ₁x² +₂ y² = 1. Значит  будет индикатрисой кривизны.

Заметим, что в точке P первая и вторая квадратичные формы для  и для F одинаковы. Отсюда следует, что нормальная кривизна поверхности и ее соприкасающегося параболоида в любом направлении одинакова.