1.6. Обобщенное однородное уравнение

Определение. Уравнение называется обобщённым однородным, если удаётся подобрать такое число k, что левая часть этого уравнения становится однородной функцией некоторой степени m относительно x, y, dx и dy при условии, что x считается величиной первого измерения, y – k-го измерения, dx – нулевого измерения и dy – ( )-го измерения.

Например, таковым будет уравнение

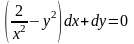. (6.1)

Действительно, при сделанном предположении относительно измерений x, y, dx и dy члены левой части и dy будут иметь соответственно измерения (–2), (2k) и (k–1). Приравнивая эти величины, получаем условие, которому должно удовлетворять искомое число k:

.

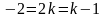Это условие выполняется при (при таком k все члены левой части рассматриваемого уравнения будут иметь измерение (–2)). Следовательно, уравнение (6.1) является обобщённым однородным.

Обобщенное однородное уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки 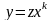, где z – новая неизвестная функция. Проинтегрируем уравнение (6.1) описанным методом. Так как , то 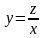, а следовательно уравнение (6.1) примет вид:

.

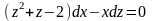Решая полученное уравнение путем разделения переменных, находим 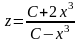, откуда 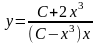. Последнее равенство определяет общее решение уравнения (6.1).

1.7. Линейные дифференциальные уравнения 1-го порядка

Определение. Линейным уравнением 1-го порядка называется уравнение, линейное относительно искомой функции и её производной. Оно имеет вид:

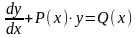, (7.1)

где и – заданные непрерывные функции от x. Если функция , то уравнение (7.1) имеет вид:

(7.2)

и называется линейным однородным уравнением, в противном случае ( ≢0) оно называется линейным неоднородным уравнением.

Линейное однородное дифференциальное уравнение (7.2) является уравнением с разделяющимися переменными:

;

;

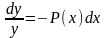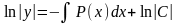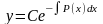. (7.3)

Выражение (7.3) определяет общее решение уравнения (7.2).

Чтобы найти общее решение уравнения (7.1), в котором функция обозначает ту же функцию, что и в уравнении (7.2), воспользуемся так называемым методом вариации произвольной постоянной, который состоит в следующем: постараемся подобрать функцию 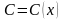так, чтобы общее решение линейного однородного уравнения (7.2) являлось решением неоднородного линейного уравнения (7.1). Тогда производная функции (7.3) примет вид:

.

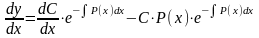Подставляя найденную производную в уравнение (7.1), получим:

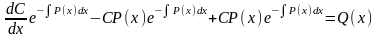
или

.

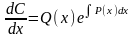Отсюда

,

где 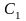– произвольная постоянная.

В результате общее решение неоднородного линейного уравнения (7.1) будет иметь вид:

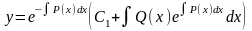. (7.4)

Заметим, что первое слагаемое в выражении (7.4) представляет общее решение (7.3) линейного однородного дифференциального уравнения (7.2), а второе слагаемое – частное решение линейного неоднородного уравнения (7.1), полученное из общего (7.4) при 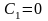. Сформулируем замеченный факт в виде теоремы.

Теорема. Если известно одно частное решение линейного неоднородного дифференциального уравнения 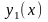, то все остальные решения имеют вид , где 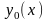– общее решение соответствующего линейного однородного дифференциального уравнения.

Однако надо отметить, что для решения линейного неоднородного дифференциального уравнения 1-го порядка (7.1) чаще применяется другой метод, иногда называемый методом Бернулли. Будем искать решение уравнения (7.1) в виде 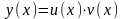. Тогда

.

Подставим найденную производную в исходное уравнение (7.1), получим:

.

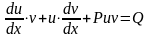Объединим, например, второе и третье слагаемые последнего выражения и вынесем функцию u(x) как общий множитель за скобку:

. (7.5)

Потребуем обращения в нуль круглой скобки:

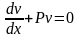. (7.6)

Решим уравнение (7.6), полагая произвольную постоянную C равной нулю:

, .

Найденную функцию v(x) подставим в уравнение (7.5), откуда получим:

.

Решая его, приходим к:

.

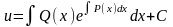Следовательно, общее решение линейного дифференциального уравнения 1-го порядка (7.1) имеет вид:

.