
- •Оглавление
- •1.1. Обыкновенные дифференциальные уравнения. Основные понятия
- •1.2. Обыкновенные дифференциальные уравнения 1-го порядка
- •1.3. Дифференциальные уравнения 1-го порядка с разделяющимися переменными
- •1.4. Однородные дифференциальные уравнения 1-го порядка
- •1.5. Дифференциальные уравнения, приводящиеся к однородным
- •1.6. Обобщенное однородное уравнение
- •1.7. Линейные дифференциальные уравнения 1-го порядка
- •1.8. Уравнение Бернулли
- •1.9. Дифференциальные уравнения в полных дифференциалах
- •1.10. Интегрирующий множитель
- •2. Дифференциальные уравнения 2-го порядка
- •2.1. Методы понижения порядка уравнения
- •2.2. Линейное дифференциальное уравнение 2-го порядка
- •2.3. Определитель Вронского
- •2.4. Структура общего решения лоду 2-го порядка
- •2.5. Лоду 2-го порядка с постоянными коэффициентами
- •2.6. Структура общего решения лнду 2-го порядка
- •2.7. Решение лнду 2-го порядка с постоянными коэффициентами со специальной правой частью
- •2.8. Метод вариации произвольных постоянных (метод Лагранжа)
- •3. Линейные уравнения высших порядков
- •3.1. Однородное уравнение
- •3.2. Линейное однородное дифференциальное уравнение с постоянными коэффициентами
- •4. Системы обыкновенных дифференциальных уравнений
- •4.1. Нормальные системы
- •4.2. Метод исключения
- •4.3. Линейные однородные системы дифференциальных уравнений (лос ду)
- •4.4. Лос ду с постоянными коэффициентами
- •4.5. Линейные неоднородные системы дифференциальных уравнений (лнс ду)
- •4.6. Метод вариации произвольных постоянных
4.6. Метод вариации произвольных постоянных
Применим метод вариации постоянных, описанный ранее, для решения линейной неоднородной системы дифференциальных уравнений (4.14).
Общее решение соответствующей однородной системы (4.5) задаётся парой выражений:
 ,
,
где и – произвольные постоянные. Будем искать решение системы (4.14) в виде
 (4.19)
(4.19)
где
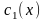 и
и
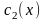 – функции, подлежащие определению.
– функции, подлежащие определению.
Подставим выражения (4.19) в систему (4.14), получим:

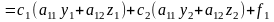 .
.
Откуда получаем
 .
.
Аналогично получаем
второе уравнение для функций
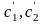 :
:
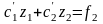 .
.
Итак, для производных имеем систему уравнений
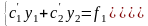 . (4.20)
. (4.20)
Определитель
последней системы есть определитель
Вронского для фундаментальной системы
решений системы (4.5), который не обращается
в нуль ни в одной точке интервала
.
Поэтому, решая систему (4.20), однозначно
определяются
 и
и
 :
:
 и
и
 .
.
Интегрируя эти выражения и подставляя результат в систему (4.19), получим ответ.
