
- •1. Модель лп на max прибыли
- •2. Модель лп на min затрат
- •4. Допустимое решение задачи лп
- •3. Границы устойчивости для коэфф-тов цел.Ф-ции.
- •5. Модель двойственной задачи.
- •6. Взаимно-обусловленные двойственные оценки
- •7. Границы устойчивости двойственных оценок
- •8. Однопродуктовая модель оптимального смешения на min затрат.
- •9. Многопродуктовая модель оптимального смешения на max прибыли
- •10. Модель оптимального раскроя с min расходами материалов.
- •11. Модель оптимального раскроя с min отходами.
- •12. Модель оптимального раскроя с учетом комплектации
- •13. Рац. Способы раскроя
- •14. Модель транспортной задачи в открытом виде.
- •15. Замкнутая транспортная задача.
- •16. Модель транспортной задачи с ограничениями на пропускную способность
- •19. Модель задачи о назначениях в стандартной форме.
- •17. Модель транспортной задачи с запретами.
- •20. Модель max дохода
- •21. Модель минимизации цел фонда.
- •22. Издержки заказа в модели управления запасами.
- •24. Детерминированная модель оптимального размера заказа.
- •25. Модель с дефицитом. Max дефицит.
- •28. Модель с фиксированным временем выполнением заказа.
- •29. Точка восстановления запаса.
- •30. Модель с производством. Max уровень запасов.
- •31. Стратегич. Игры. Седловая точка. Нижняя и верхняя цена игры.
- •38. Вероятность завершения проекта в установленный срок.
- •32. Доминирование стратегий. Мат. Ожидание выигрыша.
- •33. Одноканальная модель массового обслуживания. Параметры моделей массового обслуживания.
- •35. Модель с ограниченной очередью. Абс. И отн. Попускная способность.
- •34. Многоканальная модель массового обслуживания. Условие, ограничивающее рост очереди.
- •37. Метод pert. Ожидаемое время выполнения проекта. Вариация времени выполнения работы проекта.
- •39. Анализ затрат pert/cost. Оценка удельных затрат на сокращение продолжительности работ.
- •41. Модель лп для игры двух лиц с нулевой суммой.
- •42. Принятие решений в условиях неопределенности.
- •43. Принятие решений в условиях риска. Ожидаемая стоимостная оценка альтернативы.
- •44. Дерево решений. Ожидаемая ценность достоверной инфо-и.
- •45. Целочисленная задача лп.
- •46. Моделирование логической взаимосвязи в задаче булевыми переменными.
- •Геометрический смысл
- •47. Понятие границы Парето.
- •48. Имитационное моделирование. Метод Монте-Карло.
45. Целочисленная задача лп.
Задачи о назначении
Представление о модели:
![]()
![]()
![]()
![]()
![]()
![]() —
определяется,
распределяется рабочий на станок или
нет (в задачах о назначении).
—
определяется,
распределяется рабочий на станок или
нет (в задачах о назначении).
Задачи с неделимостью
Представление о модели:
![]()
![]()
![]()
![]() (целые).
(целые).
Задачи с булевыми переменными
![]() ;
;
![]() — j-й
проект (определяется, выполняется он
или нет).
— j-й
проект (определяется, выполняется он
или нет).
46. Моделирование логической взаимосвязи в задаче булевыми переменными.
;
- j-й проект (определяется, выполняется он или нет).
Геометрический смысл
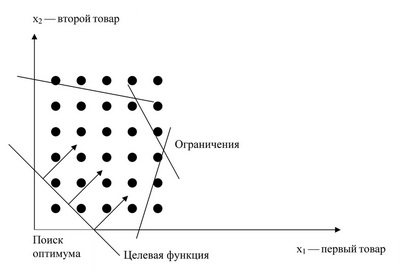
Используется метод ветвей границ — область делится на несколько частей.
Пример.
![]()
![]()
Условие взаимоисключения
![]() - данные выражения
означают, что только одна переменная
получит решение
- данные выражения
означают, что только одна переменная
получит решение
![]()
Условие взаимообусловленности
Выражение![]() означает,
что, если реализовать проект k,
то j
должно быть обязательно произведено.
Причем
означает,
что, если реализовать проект k,
то j
должно быть обязательно произведено.
Причем
![]() .
Если j
– ое значение должно получить такое же
значение, как и k,
то
.
Если j
– ое значение должно получить такое же
значение, как и k,
то
![]() .
.
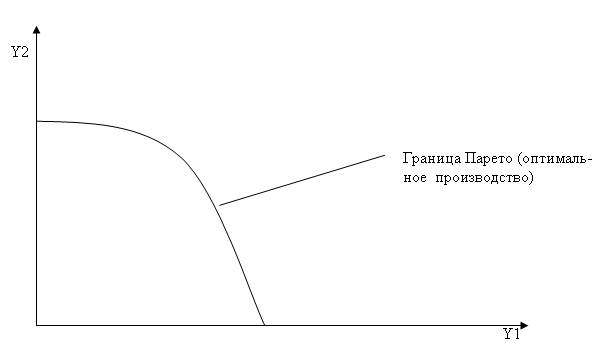
47. Понятие границы Парето.
Оптимальность по Парето — такое состояние системы, при котором значение каждого частного критерия, описывающего состояние системы, не может быть улучшено без ухудшения положения других элементов, т.е. решение называется оптимальным по Парето, если оно равномерно неулучшаемо: нельзя найти другое решение, лежащее в допустимой области, которое по всем критериям будет не хуже данного, а по какому-нибудь одному будет лучше. Множество состояний системы, оптимальных по Парето, называют «множеством Парето», «множеством альтернатив, оптимальных в смысле Парето», либо «множеством оптимальных альтернатив». Ситуация, когда достигнута эффективность по Парето — это ситуация, когда все выгоды от обмена исчерпаны.
48. Имитационное моделирование. Метод Монте-Карло.
![]()
S1 - первоначальное состояние системы (система 1);
S2 - новое состояние системы (система 2);
I - факторы, внутренние и внешние, влияющие на систему 1, под действием которых она переходит в систему 2.
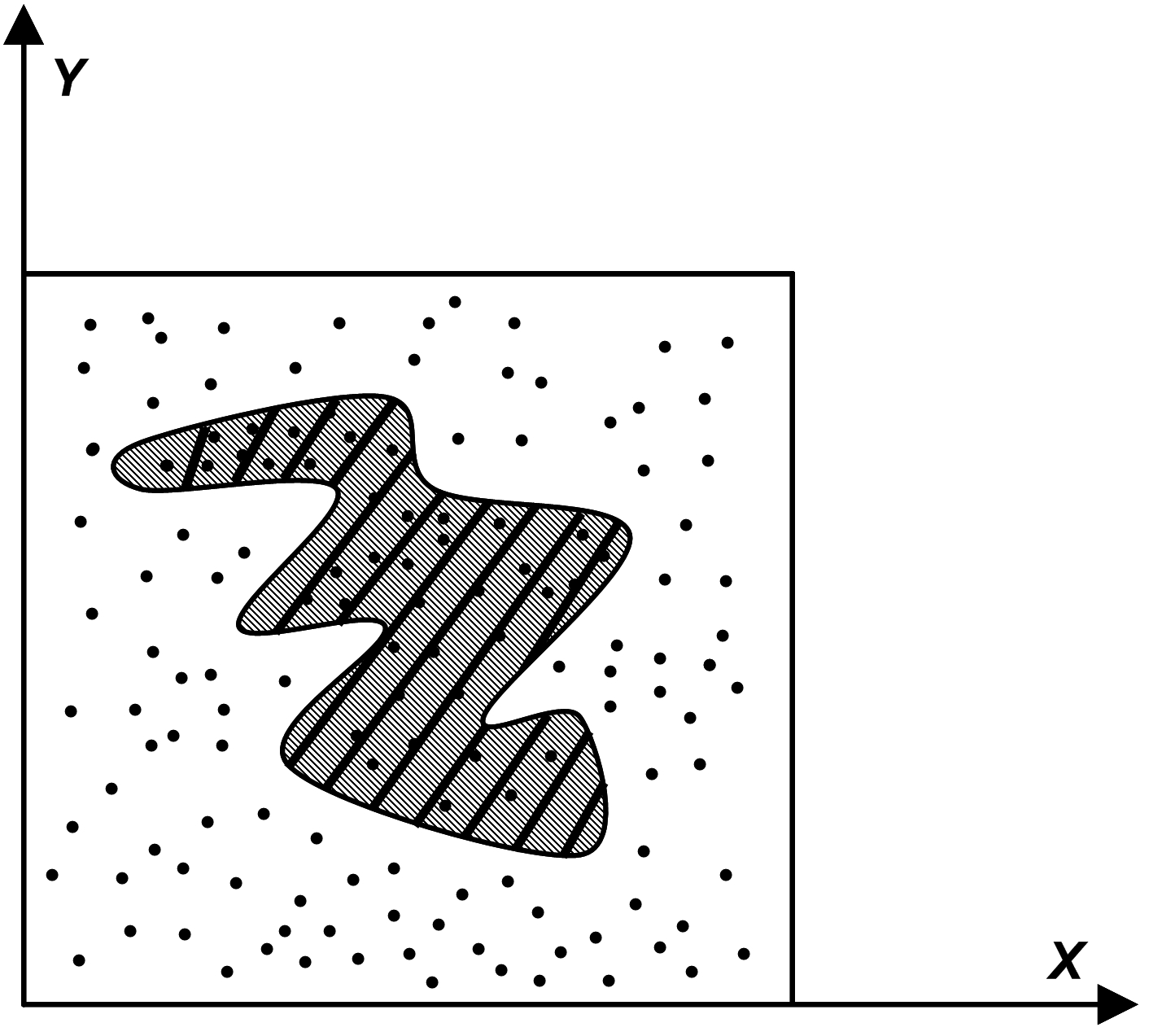
![]() где
где
![]() - количество точек,
попавших в фигуру;
- количество точек,
попавших в фигуру;
![]() -
общее количество точек.
-
общее количество точек.


![]() — критерий Стьюдента,
количество стандартных ошибок при
заданном уровне значимости
— критерий Стьюдента,
количество стандартных ошибок при
заданном уровне значимости ![]() ;
;
![]() — дисперсия
случайной величины
— дисперсия
случайной величины
![]() ;
;
![]() — несмещенная
оценка.
— несмещенная
оценка.
Y1
