4.1.2 Расчет с учетом влияния переменной нагрузки
Определяем запас прочности по нормальным напряжениям:
,
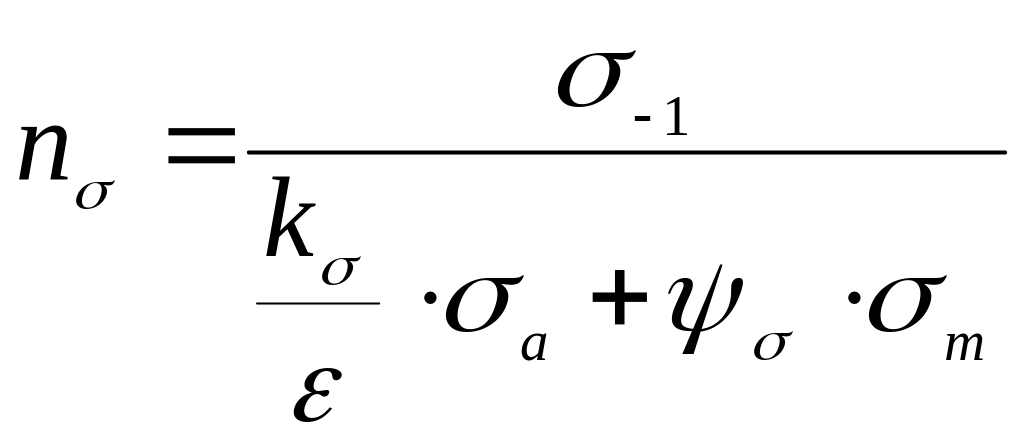где
– предел выносливости при изгибе,
.
,
,
– предел прочности при растяжении,
,
(
).
,
.
– эффективный коэффициент концентрации
напряжений при
изгибе,
(рис. П.1, П.2 [1, стр. 405]).
– коэффициент влияния абсолютных
размеров,
(рис. П.5 [1, стр. 405]).
– амплитуда нормальных напряжений,
.
,
,
– наибольшее нормальное напряжение,
,
,
– наибольший изгибающий момент в
сечении,
.
,
,
– наибольшая реакция опоры,
,
(таблица 6).
,
;
,
.
– наименьшее нормальное напряжение,
.
,
,
– наименьший изгибающий момент в
сечении,
.
,
,
– наименьшая реакция опоры,
,
(таблица 6).
,
;
,
;
,
.
– коэффициент, учитывающий асимметрию
цикла, (
);
– среднее значение нормальных напряжений
,
;
,
;
.
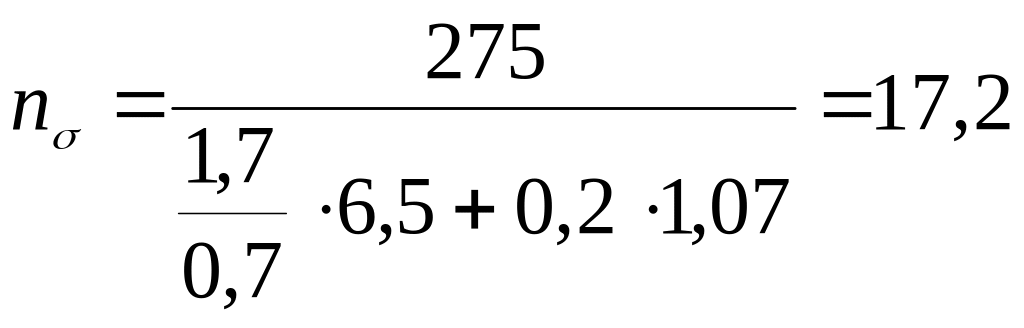Определяем запас прочности по касательным напряжениям:
,
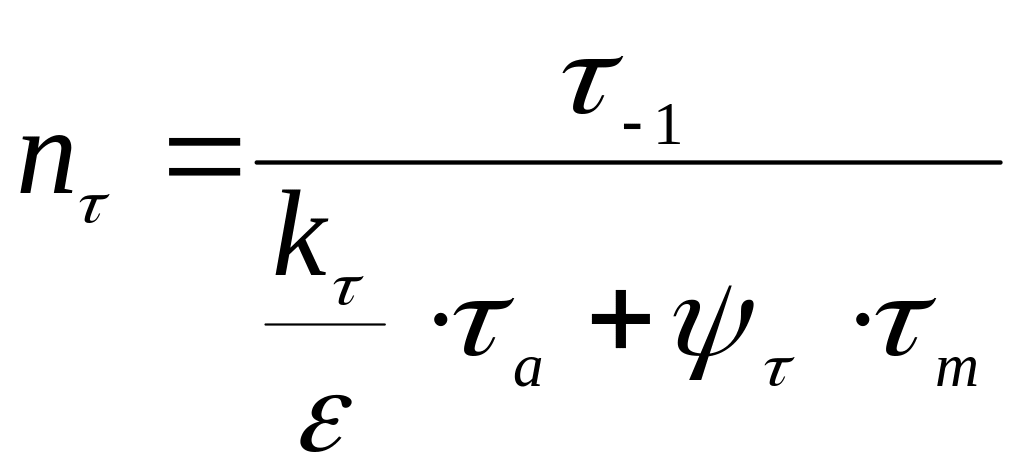где
– предел выносливости при кручении,
.
,
;
,
.
– эффективный коэффициент концентрации
напряжений при
кручении,
(рис. П.3, П.4 [1, стр. 405]).
– амплитуда тангенциальных напряжений,
.
,
,
– наибольшее касательное напряжение,
.
,
,
– наибольший крутящий момент в сечении,
.
,
,
,
.
– наименьшее касательное напряжение,
.
,
,
– наименьший крутящий момент в сечении,
.
,
,
,
;
,
.
– коэффициент, учитывающий асимметрию
цикла, (
);
– среднее значение касательных
напряжений.
,
;
,
;
.
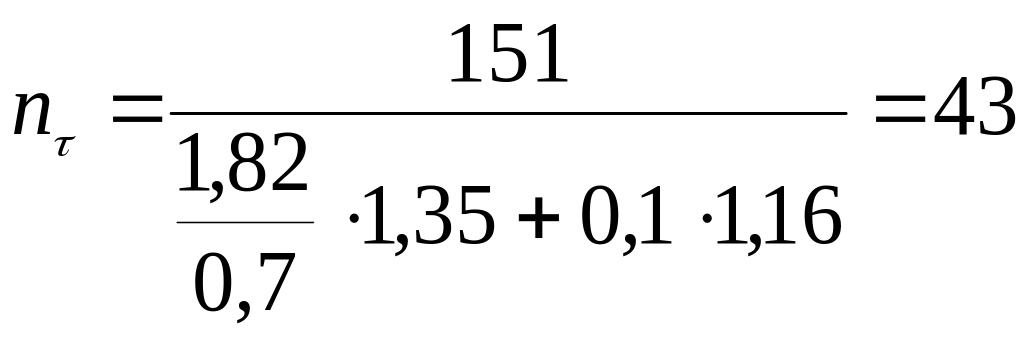Определяем общий запас прочности при наличии сложного напряженного состояния:
;
.
Допускаемые
значения
.
4.1.3 Расчет вала на жесткость
Прогибы коленчатого
вала рассчитываем графоаналитическим
методом. Как и в расчете по статическим
нагрузкам, принимаем, что максимальным
прогибам вала соответствуют максимальные
силы в цилиндре 3 при
.
Графическая часть приведена на рис. 6 и
рис. 7. На схему вала, вычерченную в
масштабе
,
наносим кроме сил
и
силы инерции противовесов и силу тяжести
полумуфты. Все силы откладываем в
соответствии с принятым правилом знаков.
,
Н
Силой тяжести муфты можно пренебречь, ввиду ее малого значения.
Составляющая силы тяжести полумуфты в плоскости, перпендикулярной плоскости колена
,
Н
Находим реакции в опорах:
В плоскости колен А'=716,3, Н, В'=2315,9, Н
В перпендикулярной плоскости А'=-2996,7, Н, В'=-6419,4, Н
Для
построения силового многоугольника
принимаем полюсное расстояние
,
причем располагаем полюс на одной
горизонтали с точкой, из которой
откладываются реакции в опорах. Построение
проводим в принятом масштабе сил
,
откладывая поочередно с учетом направления
силы и реакции в опорах, начиная с реакции
в левой опоре. Начало каждой силы соединим
силовыми лучами с полюсом. Веревочный
многоугольник, представляющий в
определенном масштабе эпюру изгибающих
моментов, строим последовательно,
проводя прямые, параллельные силовым
лучам. Первая прямая проводится от точки
пересечения с линией действия реакции
до пересечения линией действия следующей
силы
.
Если построение выполнено правильно,
точка пересечения последнего луча с
линией действия
должна лежать на одной горизонтали с
начальной точкой.
Второй веревочный многоугольник, представляющий нагрузку на вал от эпюры изгибающих моментов, строим по фиктивным силам. Разбиваем эпюру изгибающих моментов вертикальными линиями на участки, где вал имеет одинаковое сечение, и по существенным изломам эпюры. Находим фиктивные силы, действующие по вертикали через центр тяжести на каждый участок. Принимаем сечение вала на всех участках постоянным, равным сечению шатунной шейки, приводя жесткость этих участков к жесткости шатунной шейки. При этом фиктивные силы вычисляем по формуле:
,
,
где
– площадь участка эпюры,
.
,
,
– длина участка эпюры,
;
и
– размеры, выражающие изгибающие моменты
на границах
участка, ;
– момент инерции сечения вала на участке
эпюры,
;
– момент инерции сечения шатунной
шейки,
.
Момент инерции круглого сечения определяем по формуле:
,
,
где
– диаметр сечения,
.
Момент инерции прямоугольного сечения определяем по формулам:
,
;
,
,
где – ширина сечения, ;
– высота сечения,
.
Определим координаты центра тяжести участков:
,
,
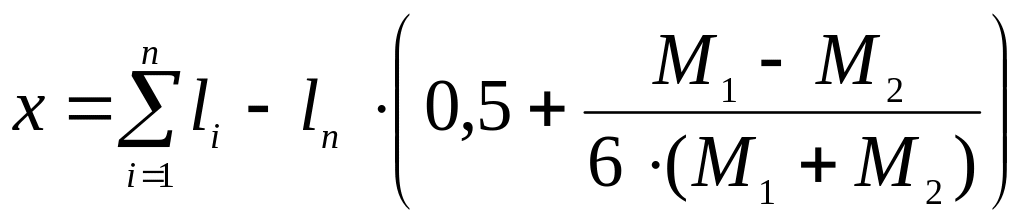где
– порядковый номер участка.
Расчетные значения
фиктивных сил и координаты их приложения
приведены в таблице 8. Для построения
силового многоугольника фиктивных сил
принимаем масштаб сил
,
полюсное расстояние
.
Строим веревочный многоугольник слева
направо. При правильном построении
многоугольника точки пересечения
первого и последнего лучей с соответствующими
линиями действия реакций опор лежат на
одной горизонтали. Через конечную точку
построения веревочного многоугольника
и точку его пересечения с линией действия
реакции левой опоры проводим нулевую
линию. Вертикальные ординаты между
нулевой линией и линией веревочного
многоугольника
и
представляют прогиб в масштабе:
Таблица
8
Значения и координаты приложения фиктивных сил
№ участка |
|
|
|
|
|
|
|
|
|
||||||||
плоскость колен |
||||||||
1 |
7 |
0 |
1,5 |
5,3 |
3,22 |
0,91 |
4,82 |
4,7 |
2 |
6 |
1,5 |
2 |
10,5 |
9,16 |
2,6 |
27,3 |
10,1 |
3 |
6 |
2 |
5 |
21 |
9,16 |
2,6 |
54,6 |
16,4 |
4 |
5 |
5 |
11,5 |
41,3 |
3,52 |
1 |
41,3 |
21,8 |
5 |
10 |
11,5 |
15 |
132,5 |
3,52 |
1 |
132,5 |
29,2 |
6 |
5 |
15 |
13 |
70 |
3,52 |
1 |
70 |
36,4 |
7 |
36 |
13 |
2 |
270 |
4,9 |
1,39 |
375,3 |
52,6 |
8 |
5 |
2 |
0,5 |
6,3 |
3,52 |
1 |
6,3 |
77 |
9 |
10 |
0,5 |
2 |
12,5 |
3,52 |
1 |
12,5 |
86 |
10 |
5 |
2 |
2 |
10 |
3,52 |
1 |
10 |
92,5 |
11 |
6 |
2 |
7 |
27 |
9,16 |
2,6 |
70,2 |
98,6 |
12 |
6 |
7 |
4 |
33 |
9,16 |
2,6 |
85,8 |
103,7 |
13 |
7,5 |
4 |
0 |
15 |
3,22 |
0,91 |
13,65 |
109,5 |
плоскость, перпендикулярная к плоскости колен |
||||||||
1 |
51,5 |
0 |
1,5 |
38,6 |
2,01 |
0,57 |
22 |
34,3 |
2 |
7 |
1,5 |
2 |
12,3 |
3,22 |
0,91 |
11,2 |
55,2 |
3 |
7 |
2 |
5 |
24,5 |
3,22 |
0,91 |
22,3 |
62,5 |
4 |
12 |
5 |
10 |
90 |
1,91 |
0,54 |
48,6 |
72,2 |
5 |
5 |
10 |
12,5 |
56,3 |
3,52 |
1 |
56,3 |
80,1 |
6 |
10 |
12,5 |
16 |
142,5 |
3,52 |
1 |
142,5 |
87,7 |
7 |
5 |
16 |
17,5 |
83,8 |
3,52 |
1 |
83,8 |
95 |
8 |
36 |
17,5 |
29,5 |
846 |
4,9 |
1,39 |
1175,9 |
117 |
9 |
5 |
29,5 |
31 |
151,3 |
3,52 |
1 |
151,3 |
136 |
10 |
10 |
31 |
23 |
270 |
3,52 |
1 |
270 |
143,3 |
11 |
5 |
23 |
18 |
102,5 |
3,22 |
1 |
102,5 |
150,9 |
12 |
12 |
18 |
7,5 |
153 |
1,91 |
0,54 |
82,6 |
158,7 |
13 |
7,5 |
7,5 |
0 |
28,1 |
0,91 |
0,91 |
25,6 |
168 |
,
,
,
,
Из графического
построения, представленного на рис. 6 и
на рис. 7, ординаты, представляющие
прогибы, равны в начале первого колена
мм,
мм;
в конце первого колена
мм
мм;
в начале второго колена
мм,
мм;
в конце второго колена
мм,
мм.
Определяем результирующие прогибы:
,
;
,
;
,
;
,
;
,
;
,
;
,
;
,
.
Принимаем, что результирующие прогибы одной шейки находится в одной плоскости.
Определяем
максимальный прогиб вала в пределах
одного вкладыша
с учетом кривизны линии прогибов для
первого колена:
,
,
где – количество шатунов на одной шейке.
,
.
Определяем максимальный прогиб вала для второго колена:
,
;
,
.
Значения
максимального прогиба в пределах одного
вкладыша шатуна необходимы для определения
минимально допустимой толщины масляного
слоя при расчете смазки.