
- •Интегрирование по частям. Примеры решений
- •Интегрирование некоторых дробей. Методы и приёмы решения
- •Сложные интегралы
- •Последовательная замена переменной и интегрирование по частям
- •Методом сведения интеграла к самому себе
- •Интегрирование сложных дробей
- •Интеграл от неразложимого многочлена 2-ой степени в степени
- •Интегрирование сложных тригонометрических функций
- •Интеграл от корня из дроби
Интеграл от корня из дроби
Интеграл, который мы рассмотрим, встречается достаточно редко, но я буду очень рад, если единственный пример данного параграфа вам поможет.
Корнями
всё начиналось, корнями и закончится.
Рассмотрим неопределенный интеграл:
![]() ,
где
,
где ![]() –
числа. Руководствуясь законом подлости,
считаем, что все эти числа коэффициенты
не равны нулю. Это уже не смешно, так
обычно и бывает.
–
числа. Руководствуясь законом подлости,
считаем, что все эти числа коэффициенты
не равны нулю. Это уже не смешно, так
обычно и бывает.
В подынтегральной функции у нас находится корень, а под корнем – дробь, в числителе и знаменателе которой располагаются линейные функции.
Метод стар – необходимо избавиться от корня. Стар и уныл, но сейчас станет веселее, поскольку придется проводить непростую замену.
Замена,
с помощью которой мы гарантированно
избавимся от корня, такова:
![]()
Теперь нужно выразить «икс» и найти, чему равен дифференциал .
Выражаем
«икс»:

Теперь
найдем дифференциал:

Зачем были эти нелепые скучные телодвижения?
Я вывел готовые формулы, которыми можно пользовать при решении интеграла вида !
Формулы
замены таковы:
![]()
Это было ни в коем случае не хвастовство, просто я не смог быстро найти эти формулы в близлежащей литературе и Сети – оказалось проще вывести. Да и может быть кто-нибудь для реферата возьмет.
Опять – двадцать пять, заключительный пример:
Пример 25
Найти
неопределенный интеграл
![]()
Проведем
замену: ![]()
В
данном примере: ![]()
![]()
Таким
образом:
![]()
Еще
куда ни шло, могло всё оказаться
значительно хуже. Такой интеграл, кстати,
уже фигурировал в Примере 13. Интегрируем
по частям:
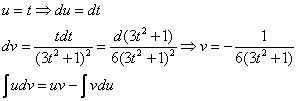
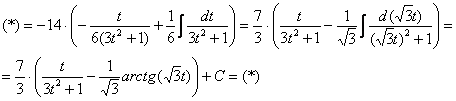
Проведем
обратную замену. Если изначально
,
то обратно:
![]()
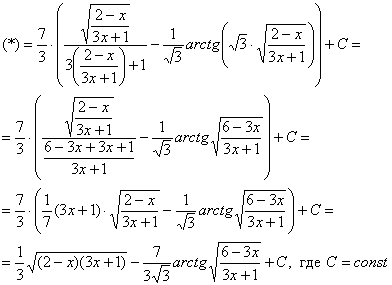
Некоторым страшно, а я это продифференцировал, ответ верный!
Иногда
встречаются интегралы вида ![]() ,
, ![]() ,
но это нужно быть либо слишком умным
либо попасть под раздачу. Идея та же –
избавиться от корня, причем во втором
случае, как все догадались, следует
проводить подстановку
,
но это нужно быть либо слишком умным
либо попасть под раздачу. Идея та же –
избавиться от корня, причем во втором
случае, как все догадались, следует
проводить подстановку ![]() и
самостоятельно выводить, чему будет
равняться дифференциал
.
и
самостоятельно выводить, чему будет
равняться дифференциал
.
Теперь вам практически любой интеграл по силам, успехов!
Решения и ответы:
Пример
2: Решение:
![]() Проведем
замену:
Проведем
замену:
![]()
![]() Интегрируем
по частям:
Интегрируем
по частям:
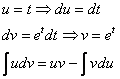

Пример
3: Ответ:
![]()
Пример
4: Ответ:
![]()
Пример
6: Решение:
![]() Интегрируем
по частям:
Интегрируем
по частям:

 Таким
образом:
Таким
образом:
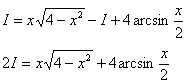 В
результате:
В
результате:
![]()
Пример
8: Решение:
Дважды
интегрируем по частям и сводим интеграл
к себе:
![]()
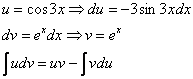
![]()
![]()
![]() Таким
образом:
Таким
образом:
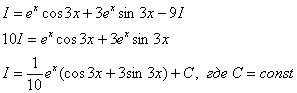
Пример
10: Решение:
![]() Проведем
замену:
Проведем
замену:
![]()

Пример
11: Решение:
![]() Замена:
Замена: ![]()

Пример
12: Решение:
![]() Замена:
Замена: ![]()
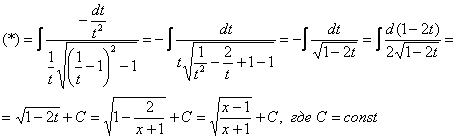
Пример
14: Решение:
![]() Дважды
используем рекуррентную формулу
Дважды
используем рекуррентную формулу ![]()
![]()
![]()
![]()
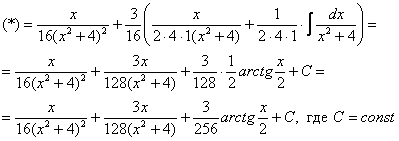
Пример
16: Решение:
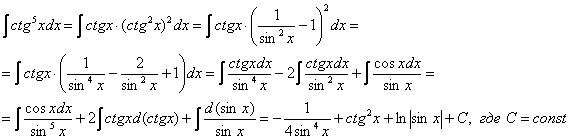
Пример
18: Решение:
![]() Используем
формулу приведения:
и
формулу двойного угла:
.
Используем
формулу приведения:
и
формулу двойного угла:
.

Пример
19: Решение:
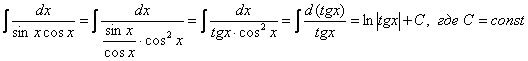
Пример
21: Решение:
–3
– 3 = –6 – целое отрицательное число
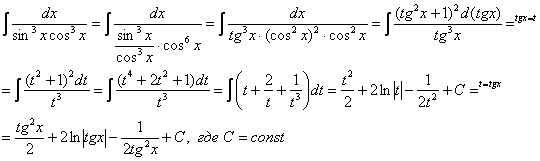
Пример
23: Решение:

Пример
24: Решение:

