Сложные интегралы
Данная статья завершает тему неопределенных интегралов, и в неё включены интегралы, которые я считаю достаточно сложными. Урок создан по неоднократным просьбам посетителей, которые высказывали пожелания, чтобы на сайте были разобраны и более трудные примеры.
Предполагается, что читатель сего текста хорошо подготовлен и умеет применять основные приемы интегрирования. Чайникам и людям, которые не очень уверенно разбираются в интегралах, следует обратиться к самому первому уроку – Неопределенный интеграл. Примеры решений, где можно освоить тему практически с нуля. Более опытные студенты могут ознакомиться с приемами и методами интегрирования, которые в моих статьях еще не встречались.
Какие интегралы будут рассмотрены?
Сначала мы рассмотрим интегралы с корнями, для решения которых последовательно используется замена переменной и интегрирование по частям. То есть, в одном примере комбинируются сразу два приёма. И даже больше.
Затем мы познакомимся с интересным и оригинальным методом сведения интеграла к самому себе. Данным способом решается не так уж мало интегралов.
Третьим номером программы пойдут интегралы от дробей, которые пролетели мимо кассы в предыдущих статьях.
В-четвертых, будут разобраны дополнительные интегралы от тригонометрических функций. В частности, существуют методы, которые позволяют избежать трудоемкой универсальной тригонометрической подстановки.
И в заключении рассмотрим интеграл от корня, под которым находится дробь, в числителе и знаменателе дроби – линейные функции.
Конечно, название урока не совсем точно, будут и не сказать, что сильно сложные интегралы. Тем не менее, крепких орешков предостаточно. Запланировано довольно много примеров, поэтому поехали.
Последовательная замена переменной и интегрирование по частям
Пример 1
Найти
неопределенный интеграл
Подынтегральная
функция представляет собой арктангенс,
под которым находится кубический корень.
Первая же мысль, которая приходит в
голову – избавиться бы от этого корня.
Данный вопрос решается путем замены
переменной, сама техника замены
специфична, и она подробно рассмотрена
на уроке Интегралы
от иррациональных функций.
Проведем замену:
После
такой замены у нас получится вполне
симпатичная вещь: 
Осталось
выяснить, во что превратится 
.
Навешиваем дифференциалы на обе части
нашей замены:
И
само собой раскрываем дифференциалы:
На
чистовике решение кратко записывается
примерно так:
Проведем
замену:
В
результате замены получен знакомый тип
интеграла, который интегрируется
по частям:
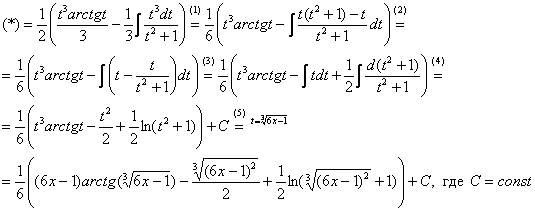
(1)
Выносим 
за
скобки. К оставшемуся интегралу применяем
прием, который рассмотрен в первых
примерах урока статьи Интегрирование
некоторых дробей.
(2) В подынтегральной функции почленно делим числитель на знаменатель.
(3) Используем свойство линейности неопределенного интеграла. В последнем интеграле сразу подводим функцию под знак дифференциала.
(4)
Берём оставшиеся интегралы. Обратите
внимание, что в логарифме можно
использовать скобки, а не модуль, так
как 
.
(5)
Проводим обратную замену, выразив из
прямой замены
«тэ»: 
Студенты-мазохисты могут продифференцировать ответ и получить исходную подынтегральную функцию, как только что это сделал я. Нет-нет, я-то в правильном смысле выполнил проверку =)
Как видите, в ходе решения пришлось использовать даже больше двух приемов решения, таким образом, для расправы с подобными интегралами нужны уверенные навыки интегрирования и не самый маленький опыт.
На практике, конечно же, чаще встречается квадратный корень, вот три примера для самостоятельного решения:
Пример 2
Найти
неопределенный интеграл
Пример 3
Найти
неопределенный интеграл
Пример 4
Найти
неопределенный интеграл
Данные
примеры однотипны, поэтому полное
решение в конце статьи будет только для
Примера 2, в Примерах 3-4 – одни ответы.
Какую замену применять в начале решений,
думаю, очевидно. Почему я подобрал
однотипные примеры? Часто встречаются
в своем амплуа. Чаще, пожалуй, только
что-нибудь вроде 
.
Но не всегда, когда под арктангенсом, синусом, косинусом, экспонентой и др. функциями находится корень из линейной функции, приходится применять сразу несколько методов. В ряде случаев удается «легко отделаться», то есть сразу после замены получается простой интеграл, который элементарно берётся. Самым легким из предложенных выше заданий является Пример 4, в нём после замены получается относительно несложный интеграл.