
- •1.Классификация уравнений в частных производных в точке (в области).
- •2.Приведение к каноническому виду уравнения 2 – го порядка в случае
- •3.Приведение к каноническому виду уравнений второго порядка с постоянными коэффициентами в случае независимых переменных.
- •4.Постановка задачи Коши. Теорема Ковалевской
- •5.Корректность постановки задачи. Пример Адамара.
- •6. Уравнения колебания струны
- •7.Малые продольные колебания упругого стержня
- •8.Малые крутильные колебания вала.
- •9. Телеграфное уравнение. Частные случаи.
- •10. Уравнение колебания мембраны
- •11. Уравнение теплопроводности
- •12.Задача Коши для одномерного волнового уравнения.
- •13.Осреднение функции на сфере и трехмерное волновое уравнение.
- •14.Задача Коши для трехмерного волнового уравнения. Формула Кирхгофа
- •15.Задача Коши для волнового уравнения. Метод спуска. Формула Пуассона.
- •16.Единственность и устойчивость решения задачи Коши для волнового уравнения.
- •17.Элементарное (фундаментальное) решение уравнения теплопроводности.
- •18.Задача Коши для уравнения теплопроводности.
- •19.Принцип экстремума для уравнений теплопроводности.
- •20.Единственность и устойчивость решения задачи Коши для уравнения теплопроводности.
- •21.Задача Штурма-Лиувилля. Свойства собственных значений и собственных функций.
- •22.Метод Фурье решения смешанных задач для однородных уравнений гиперболического и параболического типа.
- •23.Самосопряженность дифференциального оператора. Формулы Грина.
- •24.Смешанные задачи для неоднородных уравнений. Задачи с неоднородными граничными условиями.
- •25.Единственность решений смешанных задач для волнового уравнения и уравнения теплопроводности.
- •26.Свободные колебания прямоугольной мембраны.
- •27.Уравнение Бесселя. Функции Бесселя.
- •28.Радиальные колебания круглой мембраны.
- •29.Крутильные колебания вала с диском на конце.
- •30.Уравнение эллиптического типа.
- •31. Определение гармонической функции. Фундаментальное решение уравнения Лапласа
- •32. Решение задачи Дирихле для ур-я Лапласа внутри и вне круга.
- •33.Внутренняя и внешняя задача Неймана для круга. Необходимое условие существования. Теорема Гаусса
- •34. Метод Фурье решения задач Дирихле и Неймана для круговых областей.
- •35. Интегральное представление произвольной функции
- •36. Свойства гармонических функций: аналитичность и теорема о среднем на сфере
- •37.Свойства гармонических функций: принцип максимума/минимума.
- •38 Единственность и устойчивость решения задачи Дирихле.
- •39. Функция Грина в задаче Дирихле.
- •40.Функция Грина в задаче Неймана.
- •41.Формула Пуассона решения внутр. Задачи Дирихле для шара
- •42.Формула Пуассона решения задачи Дирихле для круга
- •43.Неравенство Харнака. Теорема Лиувилля
- •44. Поведение производных гармонической функции на бесконечности.
- •45. Единственность решения задачи Неймана.
- •46.Потенциалы:объемный, простого слоя, двойного слоя.
- •47. Свойства объемного потенциала
- •48. Свойства потенциала простого слоя
- •49.Свойства потенциалов двойного слоя.
- •50.Сведение краевых задач к интегральным уравнениям
33.Внутренняя и внешняя задача Неймана для круга. Необходимое условие существования. Теорема Гаусса
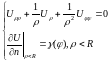 -
задача
Неймана для круга. Если
-
задача
Неймана для круга. Если
 -
внутренняя задача. Если
-
внутренняя задача. Если
 -
внешняя задача. Ф-ция
-
внешняя задача. Ф-ция


 .
Эта ф-ция будет гармонической внутри
круга любого радиуса. Надо подобрать
.
Эта ф-ция будет гармонической внутри
круга любого радиуса. Надо подобрать
 т.о., чтобы при
т.о., чтобы при
 производная по нормали от нашего ряда
совпадала с разложением ф-ции
производная по нормали от нашего ряда
совпадала с разложением ф-ции
 в ряд по косинусам и синусам кратных
углов.
в ряд по косинусам и синусам кратных
углов.


 ,
т.е. свободный член в произ-ой по нормали
отсут-ет, то внутр. задача Неймана имеет
реш-е при вып-ии усл-я:
,
т.е. свободный член в произ-ой по нормали
отсут-ет, то внутр. задача Неймана имеет
реш-е при вып-ии усл-я:
 .
Если это вып-ся , то реш-е внутр. зад.
Неймана запишется:
.
Если это вып-ся , то реш-е внутр. зад.
Неймана запишется:
 .
В этом реш-ии
.
В этом реш-ии
 - произвольная const,
поэтому реш-е внутр. З.Н. определено с
точностью до const.
В случае внешней задачи её реш-е ищем в
виде:
- произвольная const,
поэтому реш-е внутр. З.Н. определено с
точностью до const.
В случае внешней задачи её реш-е ищем в
виде:



 .
Реш-е внешней задачи Неймана:
.
Реш-е внешней задачи Неймана:

Интегральная теорема Гаусса.
При изучении смешанных задач в рассмотрение был введен оператор

При д-ве самосопряженности этого оп-ра была получена первая ф-ла Грина:

 .
Пусть Х2=U,
X2=V.
.
Пусть Х2=U,
X2=V.

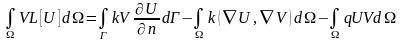
 -
вторая формула Грина. Если оп-р L[U]
=∆U,
то 2-ая ф-ла Грина имеет вид:
-
вторая формула Грина. Если оп-р L[U]
=∆U,
то 2-ая ф-ла Грина имеет вид:

Будем
считать, что ф-ция U
явл. гармонической в Ω, а ф-ция V=1.
Тогда ∆U=0,
∆V=0.
 .
Последнее выражение – матем. запись
теоремы Гаусса.
.
Последнее выражение – матем. запись
теоремы Гаусса.
34. Метод Фурье решения задач Дирихле и Неймана для круговых областей.
 .
Будем искать реш-я, кот. представляются
в виде
.
Будем искать реш-я, кот. представляются
в виде
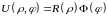
 ;
;
 ;
;
 ;
;
 ;
;
 -
аналог задачи Штурма-Лиувиля.
-
аналог задачи Штурма-Лиувиля.

 ;
;
 ;
;
 .
.
Ур-ие по R:
 ;
;
 ;
;
 ;
; ;
;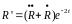 ;
; ;
; Пусть
Пусть




З аметим,
что полученное решение позволяет решить
задачу Дирихле для кольца
аметим,
что полученное решение позволяет решить
задачу Дирихле для кольца




Получим систему:
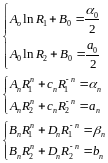
.
35. Интегральное представление произвольной функции
Теорема:
Если ф-ция U(x),
непрер. в обл. Ω, имеет в ней непрер.
вплоть до границы произв. 1-ого порядка
и непрер. в обл. Ω произв. 2-ого порядка,
то


◄
-фундаментальное
решение уравнения Лапласа. n
– размерность пространства, |Sn|
- площадь сферы единичного радиуса в
n-мерном
пространстве.
Известно, что функция En(x,ξ) явл. гармонической везде, исключ. т. ξ=x, где она обращ. в ∞. Вспомним вторую формулу Грина:
Эта формула справедлива и для случая областей, в кот. граница представляется объединением 2 границ. Во второй ф-ле Грина положим V=E и запишем её для случая объединения 2-х границ

 Пусть
имеется произв. обл. Ω. Возьмем в ней т.
х, окружим шаром, площадь шаровой пов-ти
S.
Обл., заключ. м-ду Г и S,
обозн. Ω1.
Пусть
имеется произв. обл. Ω. Возьмем в ней т.
х, окружим шаром, площадь шаровой пов-ти
S.
Обл., заключ. м-ду Г и S,
обозн. Ω1.


Устремим ε→∞. ε-радиус сферы.

т.к.
в обл. Ω1
ф-ция En(x,ξ)
гармонич. и => ∆En(x,ξ)=0.
Отметим, что интеграл по Г от ε не зависит
и не меняется при ε→0. Остается найти
 .Найдем
.Найдем











Т.к.
площадь пов-ти сферы радиуса R
в n-мерном
пр-ве равна S=|Sn|Rn-1,
т.о.
 среднее
значение ф-ции на сфере радиуса ε.
среднее
значение ф-ции на сфере радиуса ε.






Т.о.

Заметим,
что если U
– гармонич., то
 - интегр. представление гармонической
ф-ции.►
- интегр. представление гармонической
ф-ции.►
36. Свойства гармонических функций: аналитичность и теорема о среднем на сфере
1. Теорема (об аналитичности гармонической функции). Ф-ция U(x) гармонич. внутри обл. Ω с границей Г имеет в этой обл. производные всех порядков.
◄ В обл. Ω возьмем произв. т. х и окружим
её некот. пов-тью σ, целиком лежащей в
обл. Ω. Т.к. U
явл. гармонич. в обл. Ω, то она явл.
гармонич. и в обл., огранич. пов-тями Г и
σ, причем в указ. обл. ф-ция U(x)
имеет непрер. произв. второго порядка.
Согласно интегр. предст. гармонич. ф-ции
можно записать

Т .к.
т. х удалена из обл. Ω, то в интегр. по Г
можно находить производные по х любого
порядка.
.к.
т. х удалена из обл. Ω, то в интегр. по Г
можно находить производные по х любого
порядка.
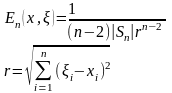
В
интеграле по пов-ти σ т. η лежит на пов-ти
σ, а т. х наход. внутри неё и

Как в предыд. случае сущ. произв. по х любого порядка, кот. можно находить дифференц. под знаком интеграла по σ. Т.к. т. х явл. произв. точкой обл. Ω, то приходим к выводу о бесконечности дифференц. ф-ций U(x) в обл. Ω, т.е. её аналитичности в этой обл.►
2. Теорема (о среднем). Среднее значение на сфере функции гармонической в шаре, ограниченном этой сферой равно значению функции в центре шара.
Док-во:
Т.к.
функция является гармонической в шаре,
то согласно интегральному представлению

Пусть
- центр шара. Подынтегральное выражение
мы высчитываем на заданной поверхности:



