
- •Высшего профессионального образования Башкирский государственный университет
- •9. Прогнозирование на основе полученной модели. Доверительный интервал прогноза.
- •1. Постановка задачи
- •2. Описание используемых данных
- •Источник данных
- •Описание данных
- •Ксерокопии источников данных
- •3. Расчёт параметров однофакторного регрессионного уравнения
- •4. Анализ адекватности однофакторного регрессионного уравнения
- •5.Прогнозирование на основе полученной модели. Доверительный интервал прогноза.
- •Двухфакторная модель
- •Анализ адекватности двухфакторного регрессионного уравнения
- •9.Прогнозирование
5.Прогнозирование на основе полученной модели. Доверительный интервал прогноза.
После
получения адекватного регрессионного
уравнения прогнозирование осуществляется
путем подстановки в регрессионное
уравнение прогнозного значения
независимой переменной (x),
то есть прогнозное значение (у)
определяется как функция: yпрогноз=f(xпрогноз),
т.е. как
![]()
Надежность прогноза сводится к проблеме построения доверительного интервала прогноза. Построение доверительного интервала прогноза для однофакторного уравнения опирается на оценку дисперсии ошибки прогноза.
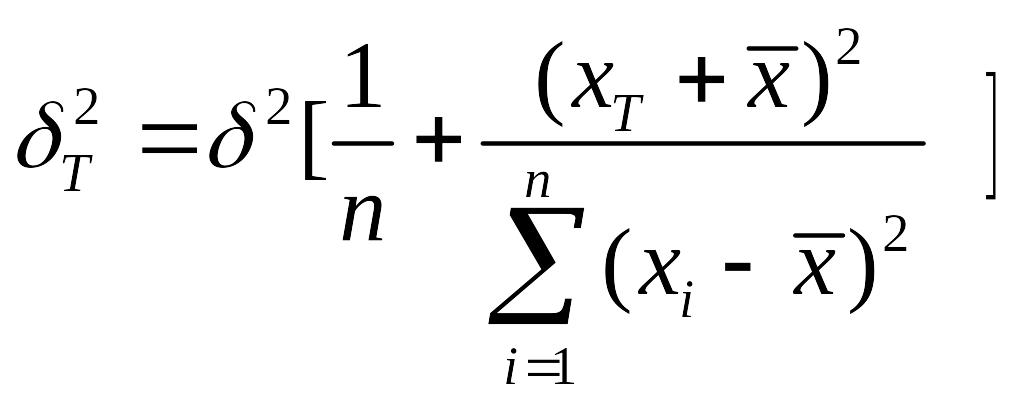 ,
где
,
где
![]() –
значение независимой переменной, для
которого определяется прогноз;
–
значение независимой переменной, для
которого определяется прогноз;
![]() -
остаточная дисперсия регрессионного
уравнения.
Используя
необходимо
построить доверительный интервал для
истинного значения прогноза
-
остаточная дисперсия регрессионного
уравнения.
Используя
необходимо
построить доверительный интервал для
истинного значения прогноза
![]() с заданной вероятностью p.
Для этого рассчитывается величина
t
по формуле:
с заданной вероятностью p.
Для этого рассчитывается величина
t
по формуле:
![]() ,
которая подчиняется t-распределению
с n-2
степенями свободы. Отсюда с заданной
вероятностью величина
t
находится в интервале:
,
которая подчиняется t-распределению
с n-2
степенями свободы. Отсюда с заданной
вероятностью величина
t
находится в интервале:
![]() Отсюда интервал для истинного значения
прогноза определяется как:
Отсюда интервал для истинного значения
прогноза определяется как:
![]()
Выводы
На основе проделанных расчетов можно сделать вывод о том, что данная модель адекватна. На основе f -статистики можно сделать вывод о существенности модели. При помощи статистики Дарбина - Уотсона выяснилось ,что автокорелляция в регрессионной модели отсутствует. А также на основе t- статистики выяснили, что х влияет на у существенно. И, наконец, наше прогнозное значении ВВП, попадает в доверительный интервал, то есть данную модель можно использовать в экономическом анализе.
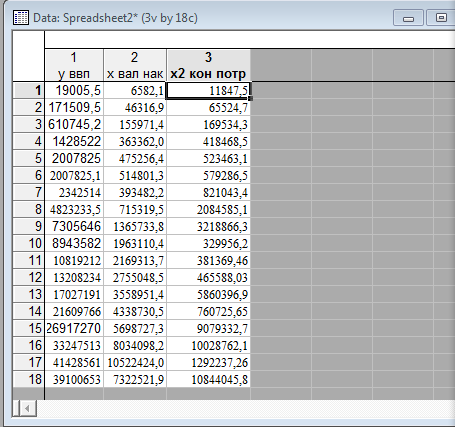
Двухфакторная модель
Исходные данные в программе STATISTICA 6.0 (все данные приведены в миллионах рублей)
Проводим анализ множественной регрессии:
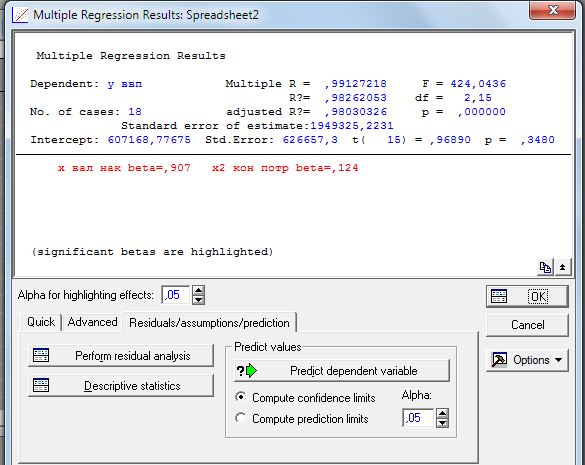
На основе полученных данных можно отметить, что коэффициент детерменации R^2 >0,7 и зависимость очень хорошая. F критерий больше его табличного значения, что говорит об отклонении гипотезы о несущественности.Степени свободы равны 2 и 15 соотвественно.
Анализ адекватности двухфакторного регрессионного уравнения
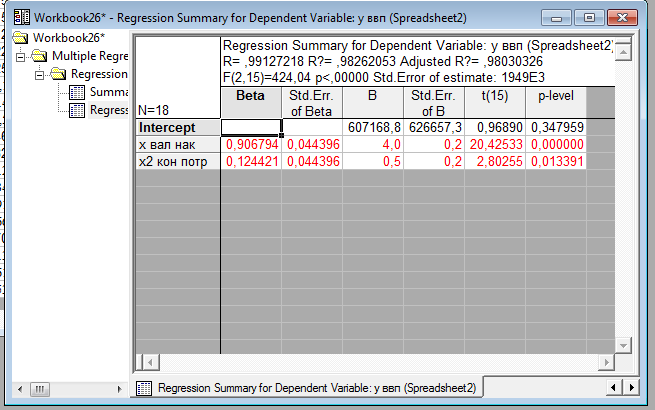
Данные этих результатов дают нам сделат ьвывод о том , что гипотезу что b=0 отвергаем и Х1 и Х2 влияют на У существенно, так как │ t расч│ > tтабл .
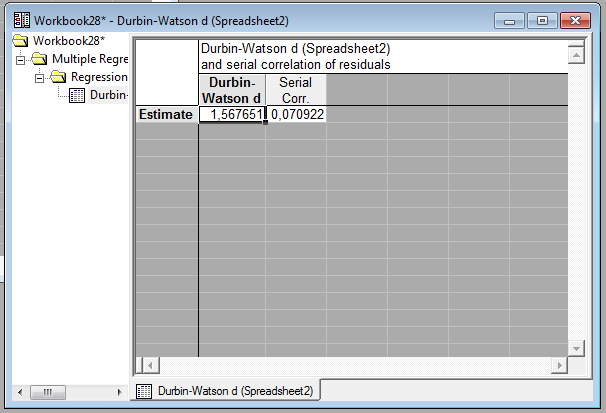
На основе этих данных можно сделат ьвывод о том , (d1=1,05; d2=1,35) что и гипотеза об отсутствии автокорреляции принимается, так как .
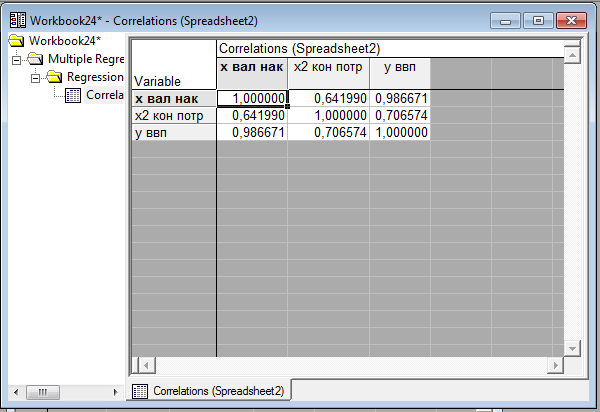
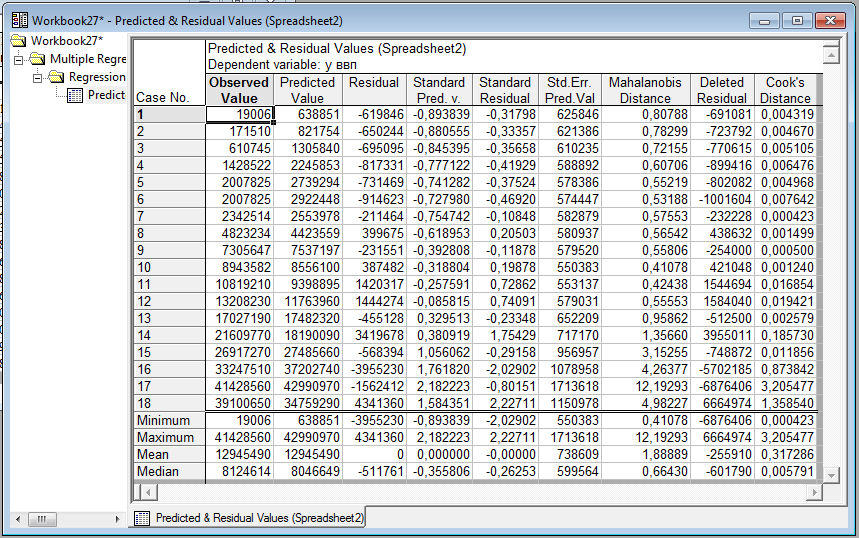
Эти результаты говорят о том что данные подобраны правильно. Зависимости между двумя влияющими на у фактором нет, то есть отсутствует мультиколлинеарность. Но в то же время они оба хорошо влияют на у.
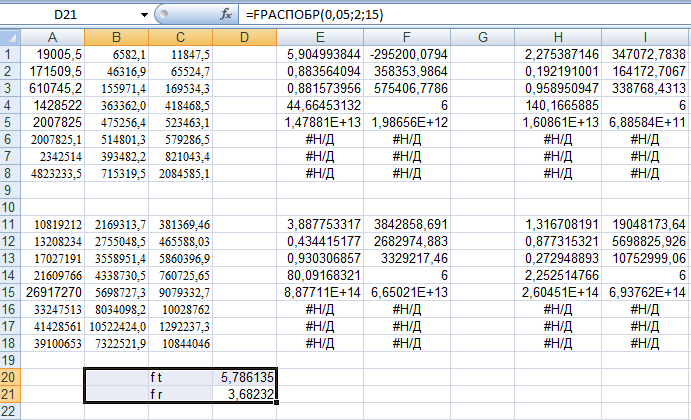
В нашем случае Fr < Ft можно считать, что дисперсия постоянна (наблюдается гомоскедастичность).
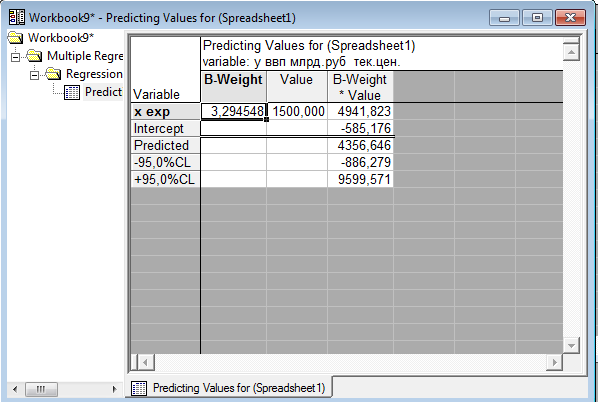
9.Прогнозирование
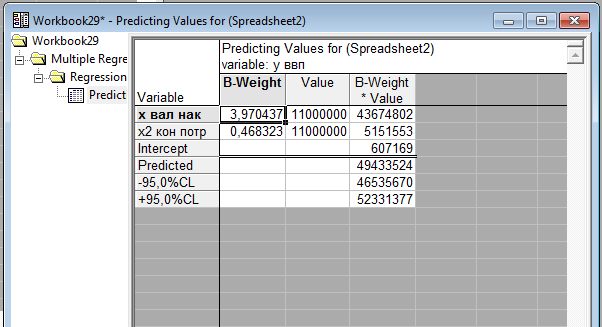
Увеличив Х максимальное на 10 % в обоих случаях , здесь приведено У прогнозное, которое попадает в доверительный интервал(49433524).
Выводы
На основе проделанных расчетов можно сделать вывод о том, что данная модель адекватна. На основе f - статистики можно сделать вывод о существенности модели. При помощи статистики Дарбина - Уотсона выяснилось, что автокорелляция в регрессионной модели отсутствует. На основе анализа корреляции можно сделать вывод об отсутствии мультиколлениарности. А также на основе t- статистики выяснили, что х влияет на у существенно. Кроме того регрессионная модель обладает гомоскедастичностью (в нашем случае Fr < Ft можно считать, что дисперсия постоянна наблюдается). И, наконец, наше прогнозное значение попадает в доверительный интервал, то есть данную модель можно использовать в экономическом анализе.
