Экзаменационный билет № 4

1. Аналоговые измерительные приборы. Общие сведения. Классификация измерительных приборов по способу преобразования электрической энергии.

2. Цифровые приборы. Основные определения. Коды, системы счисления. Погрешности цифровых приборов.

1. Аналоговым измерительным прибором называют прибор, информативный параметр выходного сигнала которого является физическим аналогом измеряемой величины. Показания аналогового прибора являются непрерывной функцией изменения измеряемой величины.

С реди приборов прямого преобразования основную группу составляют электромеханические приборы, принцип действия которых заключается в преобразовании электромагнитной энергии в механическую энергию перемещения подвижной части. Обобщенная структурная схема такого прибора представлена на рис. 8.1 и состоит из измерительной цепи 1, измерительного механизма (ИМ) 2 и отсчетного устройства 3.

Измерительная цепь 1 служит для преобразования измеряемой электрической величины X (напряжения, тока, мощности и т. п.) в некоторую промежуточную электрическую величину Х₁ (ток или напряжение), функционально связанную с величиной X и непосредственно воздействующую на ИМ 2. В ее составе могут быть и преобразователи: шунты, делители напряжения и т. п. С целью повышения чувствительности прибора и расширения диапазона измерений в сторону малых значений измеряемых величин измерительная цепь содержит электронные узлы. Такие приборы в отличие от обычных аналоговых приборов прямого преобразования называют электронными.

Измерительный механизм, состоящий из подвижной и неподвижной частей, предназначен для преобразования электромагнитной энергии величины Х₁ в механическую, необходимую для перемещения (углового либо линейного) подвижной части.

П од действием измеряемой величины в ИМ возникает вращающий момент, значение которого может быть определено как

где — изменение энергии электромагнитного поля, необходимое для выполнения работы дА по перемещению подвижной части на угол дα .

Для того чтобы угол поворота α подвижной части был однозначно связан со значением измеряемой величины, в приборе при повороте подвижной части создается противодействующий момент, направленный навстречу вращающему и зависящий от угла поворота.

У механизмов с подвижной частью на керновых опорах противодействующий момент создается с помощью спиральных пружин, а с подвижной частью на растяжках — за счет упругих свойств растяжек. Во всех этих случаях , где W – удельный противодействующий момент; α – угол поворота подвижной части.

Противодействующий момент может создаваться не только механическим способом, но и электрическим. В так называемых логометрических ИМ имеются две закрепленные под некоторым углом рамки, в которых при протекании через них электрического тока возникают два вращающих момента: причем . Поскольку они направлены навстречу друг другу, один из них можно рассматривать как противодействующий.

На подвижную часть, выведенную из установившегося положения на некоторый угол , будет действовать устанавливающий момент м_уст , значение которого определяется разницей между вращающим и противодействующим моментами. Устойчивость установившегося положения характеризуют по значению удельного устанавливающего момента.

Д ля ускорения процесса достижения установившегося отклонения ИМ создается момент успокоения М_у, который направлен навстречу движению и пропорционален угловой скорости подвижной части ИМ:

где Р — коэффициент успокоения.

С этой целью в ИМ вводится успокоитель: магнитоиндукционный, воздушный либо жидкостный.

Магнитоиндукционный успокоитель состоит из постоянного магнита , подвижного сектора из неферромагнитного проводникового материала и магнитопровода . В подвижном секторе при его перемещении в поле постоянного магнита наводится э. д. с., которая создает в нем ток, взаимодействующий с потоком постоянного магнита, образуя при этом момент успокоения.

Элементами воздушного успокоителя являются легкое подвижное крыло, укрепленное на оси подвижной части, и камера успокоителя. Воздушное успокоение основано на использовании явления вязкого трения.

Жидкостные успокоители применяют, если необходимо получить значительный коэффициент успокоения, либо в том случае, когда введение дополнительной детали в форме крыла воздушного успокоителя приводит к недопустимому увеличению момента инерции подвижной части ИМ. Жидкостные успокоители бывают двух видов. У одних вся подвижная часть ИМ помещена в футляр с жидкостью — маслом либо спиртом. У других — успокоитель капельный. В узкой щели между подвижным и неподвижным кольцами капля практически несохнущей (время 50 %-ного высыхания — до 50 лет) кремнийорганической жидкости надежно удерживается силами поверхностного натяжения. В зависимости от вязкости жидкости достигается разная степень успокоения.

2. Цифровыми (ЦИП) называют приборы, автоматически вырабатывающие дискретные сигналы измерительной информа­ции, показания которых представляются в цифровой форме. В цифровых приборах в соответствии с размером измеряемой величины образуется код, а затем в соответствии с кодом значение измеряемой величины представляется на отсчетном устройстве в цифровой форме. Код — условные сигналы (обычно электрические). Код может подаваться в цифровое регистрирующее устрой­ство, вычислительную машину или другие автоматические устрой­ства. Цифровой прибор включает в себя два обязательных функци­ональных узла: аналого-цифровой преобразователь (АЦП) и цифровое отсчетное устройство (ЦОУ). АЦП выдает код в соответствии со значением измеряемой величины, а цифровое отсчетное устройство отражает это значе­ние в цифровой форме. В настоящее время получили применение аналого-дискретные измерительные приборы (АДИП). В отличие от ЦИП в этих приборах используют квазианалоговые отсчетные устройства, т. е. устройства, в которых роль указателя выполняет светящаяся полоса или светящаяся точка, меняющие дискретно свою длину (полоса) или положение (точка) относительно шкалы. Квази­аналоговые отсчетные устройства управляются кодом. При рассмотрении вопросов, общих для ЦИП, АЦП и АДИП вводится понятие цифровое измерительное устройство (ЦИУ), под которым понимается любое из указанных средств измерений. Для образования кода непрерывная измеряемая величина в ЦИУ дискретизируется во времени и квантуется по уровню. Дискретизацией непрерывной во времени величины х {t) на­зывается операция ее преобразования в прерывную во времени, т. е. величину, значения которой отличны от нуля и совпадают с соответствующими значениями х (t) только в определенные моменты времени. Промежуток между двумя соседними момента­ми времени дискретизации называют шагом дискретизации, кото­рый может быть постоянным или переменным. Квантованием по уровню непрерывной по уровню величины х (t) называют операцию ее преобразования в квантованную величину х_к. Фиксированные значения квантован­ной величины называют уровнями квантования, разность между двумя ближайшими уровнями — ступенью, или шагом квантова­ния, или квантом.

Системы счисления, коды. В ЦИУ кодирование производится по определенному правилу, например с использованием системы счисления.

В привычной для нас десятичной системе счисления любое целое число N может быть представлено в виде:

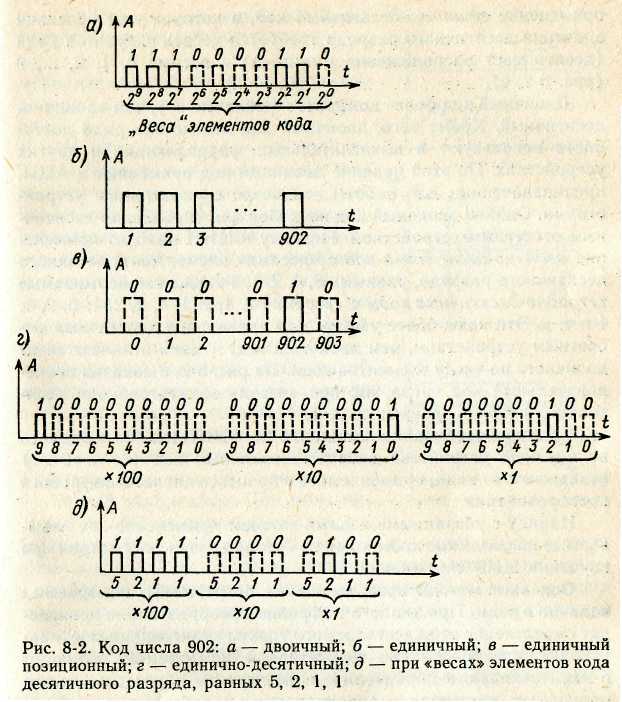
где n — число разрядов; k_i — коэффициент, принимающий зна­чения 0, 1,2,..., 9 (используется 10 различных символов). Напри­мер, число 902 можно представить в виде суммы: 9*10² + 0*10¹+ 2*10°. Любое целое число N можно выразить также в двоичной системе:

где п — число разрядов;k_i— коэффициент, принимающий зна­чения 0 и 1 (используются два символа). Например, то же число 902 в двоичной системе: 1*2⁹ + 1*2⁸ + 1*2⁷ + 0*2⁶ + 0*2⁵ + 0*2⁴ + 0*2³+1*2²+1*2¹ + 0*2°. Для уп­рощения записи указывают только коэффициенты ki, располагаемые в соответствии с порядком следования разрядов, т. е. в упро­щенном виде число 902 в двоичной системе равно 1110000110. Наиболее простая система счисления — единичная, имеющая один символ (цифра 1), при помощи которого можно выразить любое число, например, следующим образом:

Число в десятичной системе счисления .... ………..1 2 3 4……..

Число в единичной системе счисления. . . . .1 11 111 1111 ...

При образовании кодов каждому символу используемой сис­темы счисления должен соответствовать свой элемент кода.

Находят применение комбинации систем счисления. Например, двоично-десятичная система строиться на сочетании признаков двоичной и десятичной системы расположение десятичных разрядов сохраняется, но цифра каждого десятичного разряда изображается в двоичной системе. Число 902 в двоично-десятичной системе: 1001 0000 0010.

В зависимости от очередности передачи элементов кода все коды разделяют на последовательные и параллельные. У после­довательного кода элементы кода передаются последовательно во времени, причем могут передаваться по одному каналу. У па­раллельного кода элементы кода передаются одновременно по различным каналам.

Если образовывать последовательный код импульсами посто­янного тока и считать, что символу 1 двоичной системы счисления соответствует наличие импульса, а отсутствие импульса соответ­ствует символу 0, то число 902 в двоичной системе счисления имеет вид, показанный на рис. 8-2, а. Каждый импульс кода в за­висимости от места (во времени) имеет определенную значи­мость — «вес». Код, построенный с использованием двоичной системы, называют двоичным кодом.

На рис. 8-2, б показан последовательный код в виде импуль­сов тока, представляющий число 902 в единичной системе счисле­ния. Такой код носит название число-импульсного или единично­го кода. Он более громоздок, чем двоичный, однако находит при­менение в тех случаях, когда измеряемая величина простыми средствами преобразуется в этот код. Достоинство этого кода заключается также в простоте суммирования импульсов кода с помощью пересчетных устройств.

Находит применение единичный позиционный код, при ис­пользовании которого число выражается положением (порядко­вым номером) элемента кода на оси времени (последовательный код). На рис. 8-2, в представлен последовательный единичный позиционный код числа 902. в практике измерений получил применение единично-десятичный код, в котором для передачи значения десятичного разряда требуется десять элементов кода (десять мест расположения импульса) с весами 0, 1, 2, .... 9 (рис. 8-2, г).

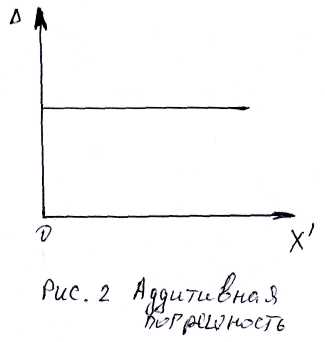
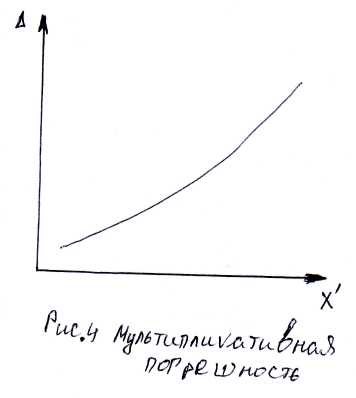
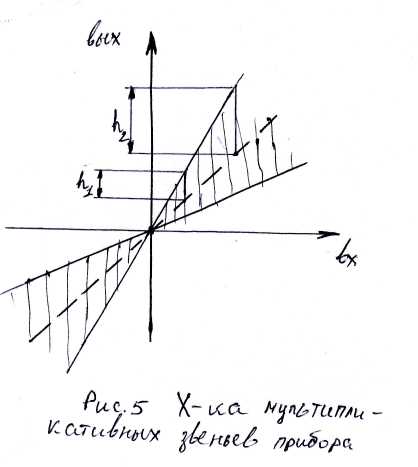
Погрешности ЦИП. При наличии аддитивной (погрешность не зависит от измеряемой величины, см рис.2,3) и мультипликативной (погрешность, возрастающая с увеличением измеряемой величины (сбивается угол), см рис.4,5) погрешностей предел допускаемой абсолютной погрешности циф­ровых средств измерения устанавливают по формуле

где X — значение измеряемой величины; а и b — положительные чис­ла, не зависящие от X.

Тогда предел допускаемой относительной погрешности определит­ся по формуле

где | Х_к | — больший по модулю из пределов измерения; с и d — положительные числа, выбираемые из ряда согласно требованиям ГОСТ 8.401—80. Коэффициенты с и d определяют по формулам

где b — коэффициент при пределе мультипликативной погрешности; а — предел аддитивной погрешности Δ₀.

Погрешность квантования основана на сравнении неизвестной величины х с известной величиной х_к (рис.8.5).

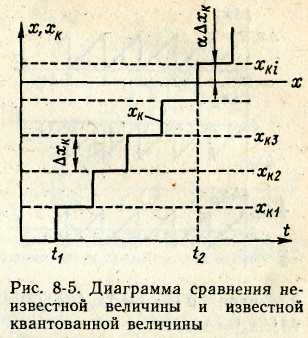
Определение отождествляемого уровня происходит при уста­новлении равенства х_к и х или, точнее, при выполнении условия х_к≥х. Выходной сигнал (показания) ЦИУ должен устанавли­ваться в соответствии с отождествляемым уровнем. Положим, что отождествление неизвестной величины х происходит с бли­жайшим большим или равным уровнем квантования, т. е. в дан­ном случае (см. рис. 8-5) с уровнем х_кi. Следовательно, в момент времени t₂ установится соотношение x_ki- х=αΔх_к, где α — ко­эффициент, значения которого могут быть в пределах от 0 до 1. Погрешность ЦИУ при этом . Эта погреш­ность есть погрешность дискретности (квантования) (Δx = Δx_д), принимающая различные значения в пределах от 0 до Δх_к. Поскольку α зависит от измеряемой величины х, которая является случайной величи­ной, то погрешность дискретности также имеет случайный ха­рактер.

Погрешность от нестабильности уровня квантования при смещении всех уровней на х_см. тогда в момент установления равенства х_к и х примем (x_ki+х_см)- х=αΔх_к. откуда погрешность ЦИУ . В этом случае появляется составляющая погрешности, обусловленная смещением уровней. Если смещение уровня зависит от номера уровня, то погрешность Δх_р зависит от х.

Погрешность сравнивающего устройства обусловлена тем, что бесконечное множество значений измеряемой величины отражается лишь ограниченным числом кодовых комбинаций ЦИУ.