3. Симплектические пространства.

Пусть V – конечномерное ВП над полем К, и : VVK кососимметрично и невырожденно. Как мы уже устанавливали (где, в каком месте?), размерность такого симплектического пространства всегда чётна. Пусть она равна 2r. Мы также устанавливали, что в таком пространстве существует симплектический базис {e₁,…,e_r;e_r+1,…,e_2r} с матрицей Грама 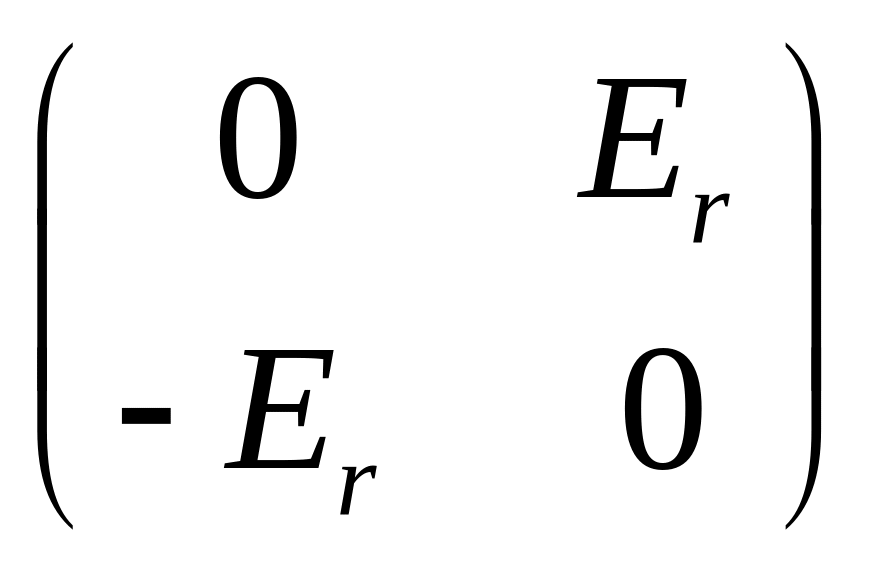, E_r=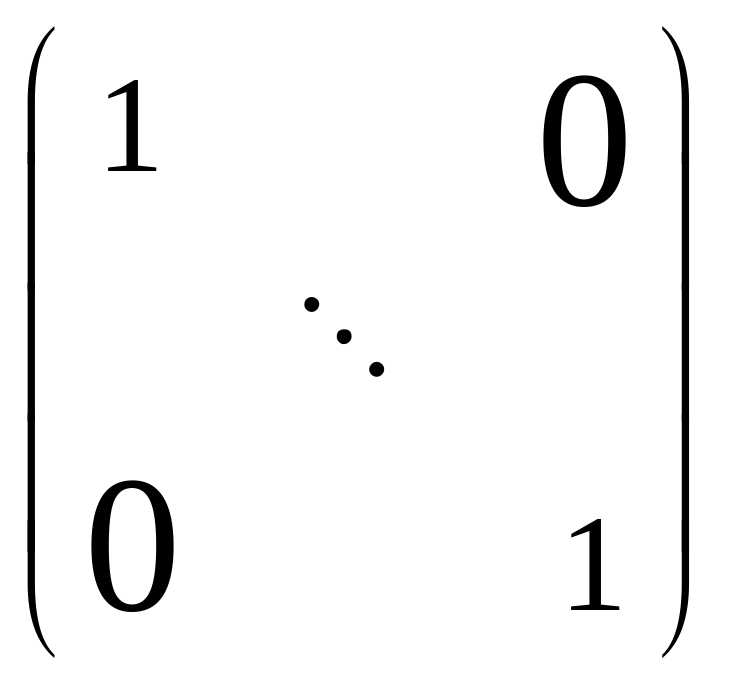 (r единиц на диагонали). Подпространство LV называется изотропным, если j_L0 (это читается так: ограничение j на пространство L тождественно равно нулю). В частности, все одномерные пространства изотропны.

Упражнение 93*. Пусть LV – изотропное подпространство размерности t. Тогда tr. (hint: j defines the isomorphism VV*.  dim L^=2r-dimL. L is isotropic  LL^).

Упражнение 94*.

Пусть LV – изотропное подпространство размерности t, t<r. Тогда L содержится в изотропном подпространстве М размерности r. (hint: prove that L = kerj_L^. Than look at symplectic basis in L^).

Итак, каждое изотропное подпространство содержится в некотором максимальном изотропном пространстве. Их, этих максимальных изотропных подпространств, может быть, разумеется, много. Оказывается, что всякое симплектическое невырожденное пространство V разлагается в прямую сумму пары своих максимальных изотропных подпространств. Сейчас в серии упражнений вы и докажите этот факт.

Итак, пусть dimV=2r, {e₁,…,e_r; e_r+1,…,e_2r} - симплектический базис V, W₁ - максимальное изотропное подпространство V; dimW₁=r. Пусть М=L{e₁,…,e_r }- линейная оболочка первых r векторов симплектического базиса и пусть dim(MW₁)=s; 0sr.

Упражнение 95.

Докажите, что существует множество номеров I{1,2,…,r}, состоящее из r-s элементов такое, что линейная оболочка N=L{e_iiI}векторов с номерами из I трансверсальна к MW₁, а именно, что N(MÇW₁)={0}.

Упражнение 96.

Положим теперь J={1,2,…,r} \ I, и W₂=L{e_i,e_r+j}; iI, jJ. Докажите, что

1. W₂, как и W₁, – изотропно.

2. W₁= W₁^; W₂= W₂^; М=М^.

3. М=MÇW₁+N ортогонально W₂ÇW₁ и W₂ÇW₁М.

4. W₂ÇW₁=(W₂ÇМ)(МW₁)= N(MÇW₁)={0}.

Упражнение 97.

Итак, вы доказали, что, если W₁ - максимальное изотропное подпространство V, то имеется другое максимальное изотропное подпространство W₂ такое, что V=W₁W₂. Докажите теперь, что билинейная форма на V индуцирует изоморфизм W₂W₁^*. Упражнение 98.

Любые пары взаимно дополнительных изотропных подпространств в V одинаково расположены, а именно: если V=V₁V₂=W₁W₂ , то существует изометрия f: VV такая, что f(V₁)=W₁; f(V₂)=W₂.

Выведите отсюда как следствие, что любые изотропные подпространства одинаковой размерности переводятся одно в другое некоей изометрией.

Упражнение 99.

Множество всех изометрий f: VV симплектического пространства V над полем F, dimV=2r, образует группу. Множество матриц, представляющих эту группу в симплектическом базисе {e₁,…,e_r; e_r+1,…,e_2r} называется симплектической группой и обозначается Sp(2r,F). Докажите, что A Sp(2r,F)  detA=1.

3. СТО (Специальная Теория Относительности)

Пространством Минковского¹ называется четырёхмерное вещественное пространство М с симметрической билинейной формой сигнатуры (1,3). Начало координат этого пространства означает событие, произошедшее «здесь и сейчас» с точки зрения некоторого наблюдателя. То есть, у другого наблюдателя – другие часы и с его точки зрения это же событие произошло в другое время. Отсутствие единого, «всемирного», универсального времени – одна из главных черт, отличающих физику высоких скоростей (физику элементарных частиц), от классической физики. В «классике» у нас для времени и пространства разные единицы измерения – метры и секунды, например. Здесь же, поскольку мы строим модель пространства-времени, нам нужны единые координаты, допускающие пересчёт единиц пространства и времени. Принято за единицу длины брать расстояние, проходимое светом (фотоном) за единицу времени, например, за 1 секунду. Уже в основу этой модели положен принцип постоянства скорости света. Итак, s=ct (c – скорость света) и после выбора единичного вектора по t скорость света (в этих единицах длины и времени) становится равной 1. Итак, мы имеем метрику (в ортонормальном базисе) (t,x₁,x₂,x₃)²=t²-x₁²-x₂²-x₃².

Заменив все три пространственных координаты одной, ; ( ), имеем:(t,x)²=t²-x².

Эта форма, как и само пространство М, называются также «псевдоевклидовыми». Таким образом, мы видим, что квадрат вектора в пространстве Минковского может быть положительным, отрицательным или нулевым. Соответственно этому, вектора эти (в физике) носят названия времениподобных, светоподобных или пространственноподобных. Если вектор, например, времениподобен, то и любой коллинеарный ему вектор времениподобен, а вся прямая L, его содержащая, называется тогда «мировой линией инерциального наблюдателя». Время между двумя точками l₁ и l₂ – событиями на этой прямой, измеренное по часам наблюдателя образующего эту прямую, относится именно к этому наблюдателю (у другого наблюдателя – другая мировая линия!) считается по формуле l₁-l₂= . Система координат в М, заданная в ортонормированном базисе называется инерциальной системой. Группа изометрий пространства М называется группой Лоренца.

Найдём теперь матрицу Р, переводящую один ортонормированный базис в другой: .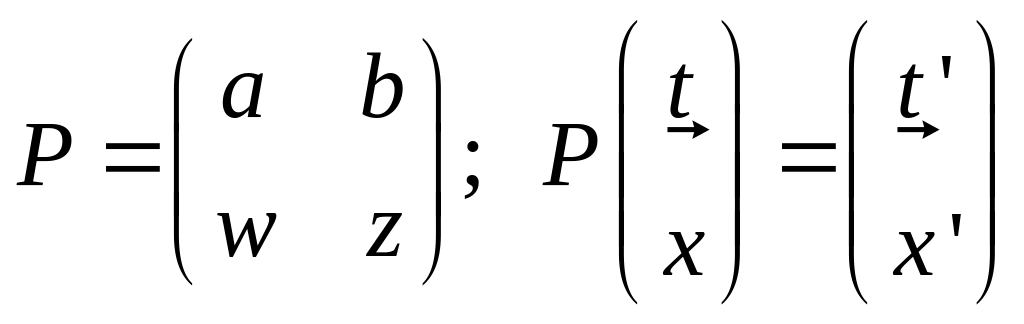

Упражнение 100.

Используя ортонормированность обоих базисов, докажите, что w=b и z=a. Итак, t’=at+bx; x’=bt+ax. Теперь определим скорость v, с которой система (t’,x’) движется относительно системы (t,x). Для этого надо расстояние, на которое вектор х’ переместился по часам системы (t,х) c момента t=0 до настоящего времени, поделить на время, которое прошло «за это время» по часам системы (t’,x’).

Упражнение 101.

Докажите, что v=b:a.

Упражнение 102.

Используя полученную формулу для скорости, и то, что длина вектора t’ равна 1, выразите обе величины а и b через скорость v. Окончательно, запишите матрицу перехода Р в виде Р=P(v). Как вы помните (вернее, - как вы должны были бы помнить!), соответствующая матрица преобразования координат L_v связана с матрицей Р формулой L_v=^tP^-1. Найдя эту матрицу, вы и найдёте так называемое преобразование Лоренца. Найдём теперь закон сложения скоростей в СТО. Пусть (t’,x’) движется со скоростью v₁ относительно (t,x), а (t’’,x’’) движется со скоростью v₂ относительно (t’,x’). Тогда .

Упражнение 103.

Найдя v такое, что вы и получите искомую формулу. Получите же её!

Проверьте, что у вас получится, если складываться будут две скорости света (два фотона летят навстречу друг другу). Наоборот, каков будет результат, если (как это обычно и бывает в наблюдаемой нами жизни, даже если речь идёт о пуле, снаряде или ракете) обе скорости малы по сравнению со скоростью света. Прочтите (или спросите у учителя физики) про опыты Майкельсона-Морли.

3. Характеристический многочлен.

Def. Пусть в конечномерном ВП над F задан линейный оператор f:VV. Выберем в V какой-нибудь базис, и пусть А – матрица оператора f в этом базисе. Назовём характеристическим многочленом оператора f (а также матрицы А) многочлен P(t)=det(tE-A). Оказывается, что

Упражнение 104*.

Характеристический многочлен не зависит от выбора базиса, и является, таким образом, инвариантом самого оператора f.

(hint: E=B^-1EB).

Упражнение 105.

Пусть P(t)=tⁿ-a_n-1t^n-1+…+(-1)ⁿa₀. Чему равны а_n-1 и а₀? Узнаёте старых знакомых?

Теперь к ним добавились новые инварианты – все остальные коэффициенты многочлена Р.

Упражнение 106.*

Докажите, что оператор f имеет собственный вектор с собственным значением   P()=0.

Def. Множество всех корней характеристического многочлена называется спектром¹ оператора f. Если среди корней нет кратных (все кратности равны 1), то спектр называется простым.

1 Другое, неудачное, на мой взгляд, название этой функции – антилинейная.

1 Вообще-то в современной литературе скалярным произведением называется любая полуторалинейная (или билинейная) форма, всё, с чем мы имели дело до сих пор. Но в старых и, особенно, в школьных учебниках, придерживаются именно такого определения. В школах, вообще-то принято даже за определение скалярного произведения брать вид, который оно принимает в ортонормальном базисе.

2 В случае эрмитовой формы называемом также неравенством Коши-Шварца. Augustin Louis Cauchy (1789-1857) - великий французский математик.

1 Hermann Minkowski, 22.06.1864 -12.01.1909. Родился в Литве, преподавал в Zurich, Göttingen где и скончался скоропостижно от аппендицита. Блестящий математик, внесший значительный вклад в комбинаторную геометрию и теорию чисел. Его лекции внимательно слушал, будучи студентом, Альберт Эйнштейн (который вообще-то не отличался прилежанием и нечасто посещал лекции других преподавателей).

1 При этих значениях оператор f(t)=tE-f является необратимым. В случае бесконечномерного пространства V это обстоятельство кладётся в основу определения спектра, как множества тех значений t, при которых оператор f(t) необратим. В случае конечномерного V оба определения совпадают.