
- •1.Матрицы и их виды.
- •2.Сложение матриц и умножение на действительное число.
- •3.Согласованные матрицы. Умножение матриц и его свойства.
- •4.Элементарные преобразования матриц. Эквивалентные матрицы.
- •9.Невырожденная матрица. Союзная матрица. Обратная матрица. Теорема о существовании обратной матрицы.
- •10.Свойства обратной матрицы.
- •11.Ранг матрицы. Свойства ранга матрицы.
- •12. Системы линейных уравнений: однородные, неоднородные, совместные, несовместные, определённые, неопределённые.
- •13.Решение невырожденных систем линейных уравнений. Матричный метод. Формула Крамера. Метод Гаусса.
- •14.Совместность системы линейных уравнений. Теорема Кронекера-Капелли.
- •15.Однородные системы линейных уравнений. Условия существования тривиального и нетривиального решений системы линейных однородных уравнений.
- •16. Определение вектора. Линейные операции над векторами.
- •17.Проекция вектора на ось.
- •18.Базис. Разложение вектора по базису. Координаты вектора. Декартова система координат. Направляющие косинусы. Деление отрезка в данном отношении
- •19.Скалярное произведение векторов. Свойства скалярного произведения и его вычисление в ортонормированном базисе
- •20.Векторное произведение векторов. Свойства векторного произведения и его вычисление в ортонормированном базисе.
- •21.Смешанное произведение векторов. Свойства смешанного произведения и его вычисление в ортонормированном базисе.
- •22.Приложения смешанного произведения.
- •31. Определение предела функции в конечной точке и на бесконечности.
- •32. Основные теоремы о пределах.
- •33.Первый и второй замечательные пределы
- •34. Непрерывность функции. Классификация точек разрыва.
- •35.Определение производной функции в точке.
- •36. Геометрический смысл производной функции в точке.
- •38.Правила дифференцирования.
- •39. Производная сложной функции.
- •41.Логарифмическое дифференцирование.
- •42.Производные функций, заданных параметрическими уравнениями.
- •43.Дифференциал функции. Применение дифференциала к приближённым вычислениям.
- •44.Правило Лопиталя.
- •45.Возрастание и убывание функций. Точки экстремума функции.
- •46.Наименьшее и наибольшее значения функции на отрезке.
- •47.Выпуклость и вогнутость графика функции. Точки перегиба.
- •48. Асимптоты графика функции.
- •49. Общая схема исследования функции и построения графика.
- •50.Первообразная функции. Неопределённый интеграл и его свойства. Таблица основных неопределённых интегралов.
- •51.Метод непосредственного интегрирования.
- •52.Метод поднесения под знак дифференциала.
- •53. Метод интегрирования по частям.
- •54.Основные типы простейших рациональных дробей.
- •55. Интегрирование рациональных дробей с помощью разложения их на простейшие дроби.
- •64. Ду высших порядков, допускающие понижение порядка.
- •65. Линейные однородные ду 2-го порядка с постоянными коэффициентами. Структура общего решения в зависимости от корней характеристического уравнения.
- •66. Линейные неоднородные дифференциальные уравнения (лнду) 2-го порядка с постоянными коэффициентами. Структура общего решения.
- •67. Понятие функции двух переменных. Область определения.
- •68. Частные производные первого порядка. Полный дифференциал.
- •69. Частные производные высших порядков.
- •70.Экстремум функции двух переменных.
19.Скалярное произведение векторов. Свойства скалярного произведения и его вычисление в ортонормированном базисе
Скалярным произведение двух векторов наз. число, равное произведению длин этих векторов на cos угла между ними: ā*в=/ā/*/в/*cos(ā,^в).
Свойства скалярного умножения:
1)скалярное умножение коммуникативное: ā*в=в*ā
2)для любого вектора скалярный квадрат = квадрату модуля: ā*ā=ā2=/ā/2
3)скалярное произведение = 0, если сомножители ортогональны или хотя бы один = 0: ā*в=0ā┴в или ā = 0 или в = 0
4)скалярное умножение обладает свойством ассоциативности относительно скалярного множителя: (λā)в=ā(λв)=λ(āв)
5)скалярное умножение дистрибутивно относительно сложения: ā(в+с)=āв+āс
20.Векторное произведение векторов. Свойства векторного произведения и его вычисление в ортонормированном базисе.
Векторным произведение векторов ā и в наз. вектор, обозначаемый с=ā×в и удовлетворяющий следующим трём условиям:
1)/ā×в/=/ā/*/в/*sin(ā,^в)
2)с┴а, с┴в
3)упорядоченная тройка ā, в, с – правая, наз. если из конца вектора с кратчайший поворот от первого вектора ā ко второму в виден против хода часовой стрелки.
Свойства:
1)от перестановки множителей, векторное произведение меняет направление на противоположное, сохраняет модуль, т.е. : ā×в=-в×ā
2)если в векторном произведении изменить знак одного из сомножителей на противоположный, то векторное произведение имеет знак, т.е. :
ā×(-в)=-ā×в
3)скалярный множитель можно выносить за знак векторного произведения: (λā)×в=λā×в или ā×(λв)=λā×в
4)(āв)×с=ā×с+в×с
5)Векторное произведение = 0, если хотя бы один из сомножителей = 0, либо сомножители комплонарны: ā×в=0ā=0 или в=0 или ā║в
6) ā×ā=0
x |
i |
j |
k |
I |
0 |
k |
-j |
J |
-k |
0 |
I |
k |
j |
-i |
0 |
21.Смешанное произведение векторов. Свойства смешанного произведения и его вычисление в ортонормированном базисе.
Смешанными векторами а, в, с наз. число обозначаемое а, в, с и определяемое как скалярное произведение вектора ā×в×с : авс= (ā×в)×с.
Свойства:
1)смешанное произведение не меняется при цикле пересечения его вектора со множителем: авс=вса=сав
2)смешанное произведение меняет знак на противоположный при перестановке любых векторов множителей: авс=-вас=вса
3)смешанные произведения не меняются при перемене местами знаков векторного и скалярного умножения : (ā×в)*с=ā*(в×с)
4)смешанные произведения не нулевых векторов равно 0 тогда и только тогда, когда векторы комплонарны : авс=0 авс- комплонарны.
22.Приложения смешанного произведения.
1)определение взаимной ориентации вектора в пространстве: если авс>0 => векторы а, в, с образуют правую тройку, если авс<0, то левую тройку.
2)установление комплонарности вектора. Векторы а, в, с – комплонарны авс=0.
3)определение объёмов в пространстве предметов: а)V- парал-да, построенного на векторах а, в, с вычисляются по формуле :V=/abc/
б)V=1/6*/abc/
в)V треугольной призмы, построенный на векторах а, в, с вычисляется по формуле: V=1/2*/abc/
23.Различные виды уравнений прямой на плоскости: по точке и нормальному вектору; общее; по точке и направляющему вектору; по двум точкам; по точке и угловому коэффициенту; в отрезках.
1. по точке и нормальному вектору А(х – х0) + В(у – у0)=0
2. общее уравнение Ах + Ву + (- Ах0 – Ву0) = 0 или Ах + Ву + С =0
3. по точке и направляющему вектору М0М║S =>М0М=t*S х-х0/m=y-y0/n
4. по двум точкам х-х1/х2-х1=у-у1/у2-у1
5. по точке и угловому коэффициенту y-y0 = k(x-x0) y=kx + b
6. в отрезках х/а+у/в=1
24.Расстояние от точки до прямой.
d=
/Ax0+By0+C/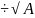 2+B2
2+B2
25.Различные виды уравнений плоскости в пространстве: по точке и направляющему вектору; общее; по трём точкам; в отрезках.
1) А(х-х0)+В(у-у0)+С(z-z0=0(по точке и напр. вектору);
2) Ах+Ву+Cz+(-Ax0-By0-Cz0)=0 или Ах+Ву+Cz+D=0 (общее уравнение);
3)
 (по
трём точкам)
(по
трём точкам)
4)
 (уравнение
плоскости в отрезках).
(уравнение
плоскости в отрезках).
26.Взаимное расположение двух плоскостей в пространстве.
Случаи взаимного расположения плоскостей:
1) Р1 ║ Р2 А1/А2=В1/В2=С1/С2≠Д1/Д2
2) Р1 совпадает с Р2 А1/А2=В1/В2=С1/С2=Д1/Д2
3) Р1 ┴ Р2 n1*n2=0 А1А2+В1В2+С1С2=0
4)
Р1 пересекает Р2 под углом γ
cos
γ = n1*n2 /n1/*/n2/=A1A2+B1B2+C1C2
/n1/*/n2/=A1A2+B1B2+C1C2 *
*
27.Различные виды уравнений прямой в пространстве: общее; по точке и направляющему вектору; по двум точкам
1)

2) =
=
 =
=

3)
4) =
=
 =
=

28.Понятие функции. Основные характеристики функции: чётная, нечётная, возрастающая, убывающая, ограниченная.
Пусть
дано 2 не пустых множества Х и У. Правило
f
по которому каждый элемент Х Х
поставлен в соответствие 1 и только 1
элементa
У
У,
наз.
функцией
и записывается : у=f(x).
Х
поставлен в соответствие 1 и только 1
элементa
У
У,
наз.
функцией
и записывается : у=f(x).
Основные характеристики:
1)Функция у=f(x) , определяемая на множестве D, наз. чётной, если любая Х D выполняет условия : -х D и f(-x)=f(x); не чётной , если любая Х D и f(-x)=-f(x)
2)Функция y=f(x) наз. возрастающей на интервале (а,в), если любое X1,X2 (а,в) Х1>X2, выполняется f(x1)>f(x2). Функция наз. убывающей если любое х1 и х2 (а,в) Х1>X2, выполняется условие f(x1)<f(x2).
3)
Функцию y
= f(x)
опр. на множество D, наз.
ограниченной
на этом множестве, если сущ. Такое число
М>0: любое х
D
=>
 M
M
29.Основные элементарные функции и их графики.
1) Степенная ф-ция: y=xα, α R
а) у=х
б) у=х2
в) у=х3
г) у=х-1=1/х
д)
у=х1/2=
2)
Показательная функция: у = ах,
а>0, a 1.
1.
а) у = ах(а>1)
б) у = ах(0<a<1)
3) Логарифмическая функция: у=logax, a>0, a 1.
a) e=logax (a>1)
б) y = logax(0<a<1)
4) Тригонометрические функции
а) у = sin x
б) y = cos x
в) y = tg x
г) y = ctg x
5) Обратные тригонометрические функции
а) y = arcsin x
б) y = arccos x
в) y = arctg x
г) y = arcctg x
30. Определение предела последовательности.
Определение. Число А наз. пределом функции f(x) при xа, если при всяком положительном числе можно указать другое положительное число , зависящее от выбора , такое, что абсолютная величина разности f(x)-А будет меньше , когда абсолютная величина разности x-a будет меньше , т.е. если числовые значения функции f(x) будут заключены в произвольной -окрестности числа А при условии, что числовые значения аргумента x взяты с достаточно малой -окрестности числа а (исключая само число а):

