
- •1.Матрицы и их виды.
- •2.Сложение матриц и умножение на действительное число.
- •3.Согласованные матрицы. Умножение матриц и его свойства.
- •4.Элементарные преобразования матриц. Эквивалентные матрицы.
- •9.Невырожденная матрица. Союзная матрица. Обратная матрица. Теорема о существовании обратной матрицы.
- •10.Свойства обратной матрицы.
- •11.Ранг матрицы. Свойства ранга матрицы.
- •12. Системы линейных уравнений: однородные, неоднородные, совместные, несовместные, определённые, неопределённые.
- •13.Решение невырожденных систем линейных уравнений. Матричный метод. Формула Крамера. Метод Гаусса.
- •14.Совместность системы линейных уравнений. Теорема Кронекера-Капелли.
- •15.Однородные системы линейных уравнений. Условия существования тривиального и нетривиального решений системы линейных однородных уравнений.
- •16. Определение вектора. Линейные операции над векторами.
- •17.Проекция вектора на ось.
- •18.Базис. Разложение вектора по базису. Координаты вектора. Декартова система координат. Направляющие косинусы. Деление отрезка в данном отношении
- •19.Скалярное произведение векторов. Свойства скалярного произведения и его вычисление в ортонормированном базисе
- •20.Векторное произведение векторов. Свойства векторного произведения и его вычисление в ортонормированном базисе.
- •21.Смешанное произведение векторов. Свойства смешанного произведения и его вычисление в ортонормированном базисе.
- •22.Приложения смешанного произведения.
- •31. Определение предела функции в конечной точке и на бесконечности.
- •32. Основные теоремы о пределах.
- •33.Первый и второй замечательные пределы
- •34. Непрерывность функции. Классификация точек разрыва.
- •35.Определение производной функции в точке.
- •36. Геометрический смысл производной функции в точке.
- •38.Правила дифференцирования.
- •39. Производная сложной функции.
- •41.Логарифмическое дифференцирование.
- •42.Производные функций, заданных параметрическими уравнениями.
- •43.Дифференциал функции. Применение дифференциала к приближённым вычислениям.
- •44.Правило Лопиталя.
- •45.Возрастание и убывание функций. Точки экстремума функции.
- •46.Наименьшее и наибольшее значения функции на отрезке.
- •47.Выпуклость и вогнутость графика функции. Точки перегиба.
- •48. Асимптоты графика функции.
- •49. Общая схема исследования функции и построения графика.
- •50.Первообразная функции. Неопределённый интеграл и его свойства. Таблица основных неопределённых интегралов.
- •51.Метод непосредственного интегрирования.
- •52.Метод поднесения под знак дифференциала.
- •53. Метод интегрирования по частям.
- •54.Основные типы простейших рациональных дробей.
- •55. Интегрирование рациональных дробей с помощью разложения их на простейшие дроби.
- •64. Ду высших порядков, допускающие понижение порядка.
- •65. Линейные однородные ду 2-го порядка с постоянными коэффициентами. Структура общего решения в зависимости от корней характеристического уравнения.
- •66. Линейные неоднородные дифференциальные уравнения (лнду) 2-го порядка с постоянными коэффициентами. Структура общего решения.
- •67. Понятие функции двух переменных. Область определения.
- •68. Частные производные первого порядка. Полный дифференциал.
- •69. Частные производные высших порядков.
- •70.Экстремум функции двух переменных.
1.Матрицы и их виды.
Матрица размером m * n –совокупность m * n чисел расположенных в виде таблицы. Из m-строк и n-столбцов.
- Матрица, все элементы, которой равны нулю наз. нулевой.
- Матрица, у которой число строк равно числу столбцов наз. квадратной.
- Квадратная матрица, у которой все элементы, кроме элемента главной диагонали равны нулю, наз. диагональной.
Диагональная матрица у которой каждый элемент =1, наз. единичной.
2.Сложение матриц и умножение на действительное число.
- сложение матриц: суммой (разностью) матрицы Am*n,=(aij) и Bm*n=(bij) наз. такая матрица Сm*n, что cij=aijbij
- умножение: произведение Am*n =(aij) на k, наз. Число b Bm*n = (bij), bij=k*aij .
3.Согласованные матрицы. Умножение матриц и его свойства.
Операции сложения матриц и умножения на число .Свойства. |
А+ В = В + А |
(А+В) + С= А(В+С) |
А+0 = А |
А-А = 0 |
Α * (А+В) = α*В + α*А |
1*А = А |
(α+β)*А = α*А + β*В |
α(β*А) = (α*β)*А |
4.Элементарные преобразования матриц. Эквивалентные матрицы.
Элементарными преобразованиями матриц, явл.:
1)перестановка двух параллельных рядов матрицы
2)умножение всех элементов, любого ряда матрицы на отличное от нуля число
3)прибавление ко всем элементам ряда матриц соответствующих элемент. параллельного ряда и умноженное на одно и тоже число.
Две матрицы называются эквивалентными, если 1 из них получается из другой с помощью элементарных преобразований и обозначается А˜ В.
5. Определители 2-го порядка.
n=2,
A2x2=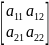 ,
det A=
,
det A=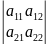 =a11
a22
– a12
a21
=a11
a22
– a12
a21
6. Определители 3-го порядка.
n=3,
A=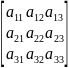 ,
,
det
A=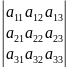 =a11
a22
a33+a21
a32
a13+a12
a23
a31-
a13
a22
a31-
a21
a12
a33-
a32
a23
a11
=a11
a22
a33+a21
a32
a13+a12
a23
a31-
a13
a22
a31-
a21
a12
a33-
a32
a23
a11
7. Миноры и алгебраические дополнение элемента определителя.
Минором элемента aij определителя порядка n называется определитель n-1-го порядка, полученный из исходного вычеркивания i-ой строки j-го столбца.
Алгебраическим дополнением элемента aij с определителем ∆ наз. Соответствующие минором взятом i+j-числа, «+» если i+j-четна, «-» если i+j-нечетна.
8.Свойства определителей.
Свойства:
1)Определитель не изменится, если его строки заменить соответствующими столбцами и наоборот.
2)Если поменять местами два параллельных ряда определителя, то определитель изменит знак.
3)Определитель с двумя одинаковыми параллельными рядами равен 0.
4)Общий множитель, какого – либо ряда можно вынести за знак определителя.
5)Определитель, у которого элементы двух рядов соответственно пропорционален, то он =0.
6)Если все элементы какого-либо ряда определителя равны 0, то и сам определитель равен 0.
7)Определитель не изменится, если к элементам одного ряда прибавить соответственно элементы другого параллельного ряда, умножить на одно и то же число.
8)Определитель равен сумме произведения элементов любого ряда на их алгебраическое дополнение.
9.Невырожденная матрица. Союзная матрица. Обратная матрица. Теорема о существовании обратной матрицы.
Квадратная матрица А наз. не выраженной, если det A0. В противном случае (det A=0) – выражденной.
Союзной матрицей А наз. матрица А*
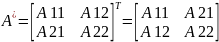
Матрица А-1 наз. обратной к матрице А, если выполняются следующие действия:
А×А-1 = А-1×А = Е, где Е – единичная матрица, того же размера, что и А.
Теорема. Для данной матрицы А, существует единственная обратная матрица А-1 detA≠0.
Формула для нахождения обратной матрицы:

