Решение уравнения методом Ньютона

Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции.

Достоинства метода Ньютона: Метод Ньютона - самый быстрый способ нахождения корней уравнений: обычно заданная точность достигается за 2-3 итерации. Очень быстрая сходимость по сравнению с методом половинного деления и методом простой итерации к заданной точности.

Недостаток: громоздкий алгоритм: на каждой итерации необходимо вычислять значение функции и ее первой производной.

Значение корня новой итерации вычисляется по формуле

Алгоритм

1. Задается начальное приближение x₀.

2. Пока не выполнено условие остановки, в качестве которого можно взять или (то есть погрешность в нужных пределах), вычисляют новое приближение: [1].

Производные функции

1. ;

2. ;

3. если >0

если <0

Точное значение корня

Первое уравнение – кубическое уравнение

Решение кубического уравнения по формуле Кардано

Кубическое уравнение в каноническом виде:

Обозначим дискриминант кубического уравнения

По формулам Кардано 3 корня уравнения определяются следующим образом:

где

При этом количество корней уравнения определяются следующим образом:

Если , уравнение имеет три действительных корня.

Если , уравнение имеет один действительный и два комплексно сопряженных корня.

Если , уравнение имеет два действительных корня. Если p = q = 0, уравнение имеет один действительный корень [2].

Разрабатываемая функция будет вычислять только первый корень. При наличии других действительных корнях будет сообщать об этом.

Наше уравнение имеет вид:

Следовательно

Вычисление корня по формуле Кардано:

float al, be,//альфа, бетта

p, q,//коэффициенты канонического уравнения

de;//дискриминант (дельта)

p = b / a;

q = c / a;

de = pow(p / 3, 3) + pow(q / 2, 2);

al = pow(-q / 2 + pow(de, 0.5), (float)1/3);

be = pow(-q / 2 - pow(de, 0.5), (float)1/3);

if(de <= 0)

cout<<"\nYravnenie imeet neskol'ko deistvitelnuh kornei.";

return al + be;

Второе уравнение – тригонометрическое уравнение

Найдем точное решение уравнения

Уравнение имеет множество корней. Нас интересует ближайший корень к точке x0, следовательно, необходимо найти ближайшее целое значение k.

Тогда точное решение будет в соответствии с найденным k:

int k;

k = (x0 - asin(-c / a) + b) / (2 * M_PI);

return asin(-c / a) + 2 * M_PI * k - b;

Третье уравнение – логарифмическое уравнение

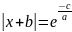
Два возможных точных решения:

Нам необходимо выбрать ближайший к x0. То есть сравниваем расстояния х1х0 и х2х0 и выбираем ближайший:

if (fabs(exp(-c / a) - b - x0) < fabs(-exp(-c / a) - b - x0))

return exp(-c / a) - b;

else

return -exp(-c / a) - b

Абсолютная и относительная погрешность вычисления

Абсолютная погрешность вычисления находится как модуль разности между точным и приближенным решением [3].

А относительной погрешностью приближённого числа называется отношение абсолютной погрешности приближённого числа к самому этому числу в процентном соотношении.

Так в нашем случае

fabs(pribl - toch) – абсолютная погрешность;

fabs(pribl - toch) / toch * 100 – относительная погрешность.

Где pribl – приближенное решение интеграла (методом левых прямоугольников), toch – точное решение интеграла.