Лекция №5

В основе метанольных топливных элементов лежит реакция:

СН₃ОН = СО + 2Н₂

CO тормозит реакцию, так как находится в адсорбированном состоянии на катализаторе и неохотно его покидает. Это уравнение каталитической реакции.

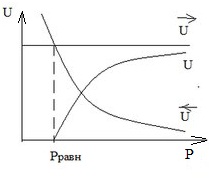
Проанализируем, как будет зависеть скорость процесса от давления, при Т=const и Х_СН3ОН=const. Для этого применим закон Дальтона:

Получаем, что скорость прямой реакции не зависит от давления, а скорость обратной реакции зависит от давления линейно.

В ычитая из U, U получаем, что для этой реакции наблюдаемая скорость уменьшается с ростом давления.

Таким образом, для данной реакции отсутствует понятие Р_опт, а любое увеличение давления, выше атмосферного, приведет к снижению скорости. Отталкиваться нужно от Р_атм.

Управление состоянием равновесия и скоростью сложных процессов.

Рассмотрим случай протекания параллельных реакций.

а₁А + b₁B = cC

a₂A + b₂B = dD

Для расчета равновесного состава реакционной смеси необходимо составить материальный баланс и установить связь между начальными мольными долями компонентов и равновесной степени превращения ключевого компонента в каждой реакции.

Для упрощения задачи примем, что суммарный мольный поток NNS = 1 моль/с, соответственно, мольные потоки исходных реагентов численно равны начальным мольным долям этих реагентов, а для упрощения таблицы примем, что мольные доли продуктов в исходной смеси равны 0.

Соответственно, производительность по компоненту А будет равна:

	а1А + b1B = cC a2A + b2B = dD
исх	ZNA	ZNB	0		1
пр-х				0
			0
ком		ZNB-b1/a1·ZNA·X1- b2/a2·ZNA·X2			W

Для расчета мольных долей компонентов конечной смеси надо разделить мольный поток каждого компонента на коэффициент изменения числа молей.

Для расчета равновесного состава составляем 2 функции.

И для нахождения величин Х1 и Х2 необходимо решать систему 2х этих трансцендентных уравнений, при этом помнить, что Х1, Х2 0 ≤ Х1+Х2 ≥ 1.

Попробуем проанализировать, как будет изменяться равновесный состав.

Экзотермическая реакция.

Kp1 больше, чем Kp2, отсюда мы можем сделать вывод, что для выполнения Х1+Х2=1 необходимо, чтобы равновесная концентрации компонента С была больше, чем концентрация компонента D.

Эндотермическая реакция.

Влияние температуры, давления и концентрации на скорость параллельных реакций.

Скорость химической реакции зависит от боль­шого числа различных факторов. Для сложных реакции, в частности для параллельных, вопрос о выборе концентраций реагентов для управления процессом не является однозначным. Рассмотрим для примера систему из двух параллельных реакций разного порядка (при постоянной температу­ре):

(II)

.

Говоря об увеличении скорости такой реакции, нужно сначала решить, какая реакция более важна, т.е. какая реакция приводит к об­разованию нужного целевого продукта. Нас интересует чаще всего не то, насколько быстро израсходуется реагент А, а насколько быстрее целевой продукт будет образовываться но сравнению с побочным про­дуктом. Пусть в рассматриваемом примере целевым является продукт пер­вой реакции R, а побочным - продукт S.

Для анализа соотношения скоростей целевого и побочных процес­сов пользуются мгновенной или дифференциальной селективностью, равной отношению скорости расходования реагента А на целевую реакцию к общей скорости расходования реагента и на целевую, и на побочные реакции. Значение дифференциальной селективности в ходе процесса в об­щем случае не остается постоянным, гак как оно определяется отноше­нием скоростей реакций, а скорость реакции по мере ее протекания ме­няется. Лишь в том случае, когда параметры процесса во времени и пространстве не меняются, φ’остается постоянной величиной.

При протекании химической реакции меняются концентрации ре­агентов и продуктов. Рассмотрим, как при изменении концентрации исходного реагента А для системы параллельных реакций (II) при постоянной температуре процесса меняется дифференциальная се­лективность φ’. Пусть целевая реакция имеет по исходному реагенту порядок n₁, а побочная реакция – n₂, тогда:

Проанализируем зависимость φ’ от концентрации реагента А. Для удобства преобразуем выражение:

Очевидно, что φ’ может быть как возрастающей, так и убывающей функцией от концентрации. Определим характер функции φ’(с_А) по знаку первой производной:

Как видно из этого уравнения, знак первой производной зависит от знака Δn. Если Δn<0, т.е. если n₁>n₂, то φ’(с_А) – возрастающая функция. Скорость целевой реакции с ростом концентрации исходного реагента возрастает значительно быстрее скорости побочной реакции и доля скорости целевой реакции в суммарной скорости возрастает.

В этом случае желаемый результат – увеличение скорости образования целевого продукта R по сравнению со скоростью образования побочного продукта S – достигается при использовании исходного реагента высокой концентрации.

При Δn>0 характер зависимости противоположный, следовательно, φ’(с_А) – убывающая функция. И более высокая концентрация достигается при низкой концентрации исходного реагента.

При Δn=0 дифференциальная селективность остается постоянной величиной при любых значениях исходных реагентов, и изменить φ’ можно только изменив соотношение к₂/к₁.

Проще всего можно повлиять на это соотношение изменив температуру проведения реакции, так как температура является одним из параметров, в наибольшей степени влияющим на скорость реакции. Рассмотрим влияние температуры, анализируя уравнение Аррениуса:

.

Можно пренебречь зависимостью предэкспоненциального множителя от температуры (RT<<Е). Уравнение Аррениуса можно представить в виде линейной зависимости: . Из анализа этой зависимости можно сделать следующие выводы:

1) Из неравномерности температурной шкалы следует, что химические реакции более чувствительны к изменениям температуры в области более низких температур.

2) Чем выше энергия активации реакции, тем более чувствительна она к изменениям температуры.

3) Рассмотрим влияние температуры на дифференциальную селективность параллельных реакций:

Для того, чтобы выделить только влияние температуры на селективность, принимаем, что n₁=n₂. Преобразуем это уравнение с учетом уравнения Аррениуса.

Пренебрегая слабым влиянием температуры на предэкспоненциальные множители в уравнении Аррениуса, считаем, что от температуры не зависит. Тогда производная положительна, если ΔЕ=Е₁-Е₂>0, и отрицательна, если ΔЕ<0.

Таким образом, если энергия активации целевой реакции превышает энергию активации побочной реакции, то с ростом температуры наблюдается возрастание дифференциальной селективности, т.е. относительно более быстрое увеличение скорости целевой реакции по сравнению с ростом скорости побочной реакции и суммарной скорости процесса. И наоборот, если Е₁<Е₂, для увеличения дифференциальной селективности φ’ нужно понижать, а не повышать температуру.

Задачи

1. Р, Н_НСl=const

2. Р , Н_НСl=const

Экзотермическая реакция

1. T, P = const

2. T V

3. P