Лекция №9 Адиабатический температурный режим.

Рассмотрим Реактор полного смешения.

Для РПС в качестве элементарного объема мы рассматриваем весь объем реактора, поэтому тепловой баланс мы можем составить для всего реактора в целом.

Тепловой баланс в стационарных условиях будет выглядеть так:

Q_вх+Q_{хим. р.}=Q_вых

Теплота расходуется на нагрев или охлаждение исходной смеси.

Q_вх рассчитывается как произведение начального мольного потока на теплоёмкость реакционной смеси на входе в реактор на входную температуру.

Q_вх=NNS·Cp_вх·T_вх

NNS [моль/с], Cp_вх [Дж/моль·К], Q_вх[Дж/с]=[Вт].

Принципиально, эту величину можно определить двумя путями:

1. путь - Разделить суммарный мольный поток, потом сложить и в результате мы получим число.

NNA·Cp_вх·T_вх NNS вычисляется на основе материального баланса

NNB·Cp_вх·T_вх

·

·

·

____________

2. путь менее экстенсивный.

Ср_вх – средняя теплоёмкость реакционной смеси на входе в реактор;

ZNI- начальная мольная доля i-го компонента; Ср_вх·ZNI – исходные вещества, реагенты, инерты, которые поступают в реактор.

NKS – мольный поток;

Нам необходимо рассчитать Т_вых, Ср_вых зависит от температуры, но мы вносим допущение

Это вносит ошибку в наш расчет, но она не заметна, так как молярная теплоёмкость веществ, по крайней мере дл веществ, находящихся в газообразной фазе, друг от друга отличаются незначительно. Отсюда, изменение состава не приведет к существенному изменению средней теплоёмкости.

Относительно температурной зависимости мы вносим ошибку и единственным смягчающим обстоятельством в уравнении для скорости процесса будет использование К, и поэтому мы в этом уравнении подставляем величины средней теплоёмкости реакционной смеси на входе в реактор.

Мы не знаем мольный поток на выходе из реактора, но мы знаем, что он учитывает коэффициент изменения числа молей реакционной смеси, который в свою очередь учитывается при расчете концентрации компонентов, входящих в уравнение скорости процесса, поэтому для первоначального расчета мы можем принять , т.е.

Изменение начального мольного потока – это проценты, теплоёмкости – доли процентов, а температуры – это разы! Вклад выходной температуры будет больше, чем двух других.

Тепловой эффект химической реакции.

q_х.р. – удельный тепловой эффект химической реакции;

а – коэффициент при ключевом компоненте;

;

, ,

Закон Гесса

Состояние равновесия мы не рассматриваем, и U_х.р. не равно 0.

Можно сократить U_х.р и получим:

Отсюда,

- адиабатический коэффициент.

Физический смысл этого коэффициента: изменение температуры реакционной смеси при полном превращении ключевого компонента.

Теперь мы получаем:

Математическая модель адиабатического РИВ

Математическая модель адиабатического РПС

Для РИВ в качестве элементарного объёма выбираем участок реагирующей среды с диаметром, равным диаметру реактора и бесконечно малой длиной l. Вывод уравнения для РИВ аналогичен выводу уравнения для РПС, за исключением выражения для объема реактора: .

Тогда примет вид:

Проектирование адиабатического РИВ.

Для экзотермической реакции

VNS, P, ZNI и T_вх = const.

В адиабатическом температурном режиме температура перестаёт быть управляющим параметром. Управляющий параметр становится температура смеси на входе в реактор.

Рассмотрим, что происходит на границах наших участков.

В том случае если V=0 X=0, T=T_вх и имеет некоторое значение отличное от нуля, производительность равна 0. Поскольку у нас входная температура имеет какое-то значение, то соответствовать этой температуре, давлению и составу будет некоторое значение равновесной степени превращения.

Если будет большой объем реактора (реакция экзотермическая), температура будет увеличиваться, и поэтому, в соответствии с принципом Ле-Шателье, по мере протекания реакции, равновесие смещается в сторону исходных веществ. А поскольку при бесконечном увеличении объема реактора мы будем приближаться к равновесной степени превращения, то скорость будет асимптотически приближаться к нулю, а производительность - к какому- то предельному значению.

Скорость химической реакции

Поскольку при протекании реакции температура будет увеличиваться, один из сомножителей будет увеличиваться, а ДС уменьшаться, при чем движущая сила уменьшается по двум причинам: увеличение температуры приводит к уменьшению константы равновесия, а изменение концентраций реагентов, а именно уменьшение концентрации исходных и увеличение концентрации продуктов, приводит к уменьшению концентрации составляющей ДС.

Отсюда мы получаем, что скорость будет проходить через экстремум и, когда рост константы скорости превышает снижение ДС, мы находимся в состоянии дали от равновесия, а если ДС мала, то величина константы скорости уде не имеет значения.

Если скорость проходит через экстремум, то зависимость X от V_p будет иметь форму вогнуто-выпуклой кривой. Точка перегиба будет соответствовать максимуму скорости.

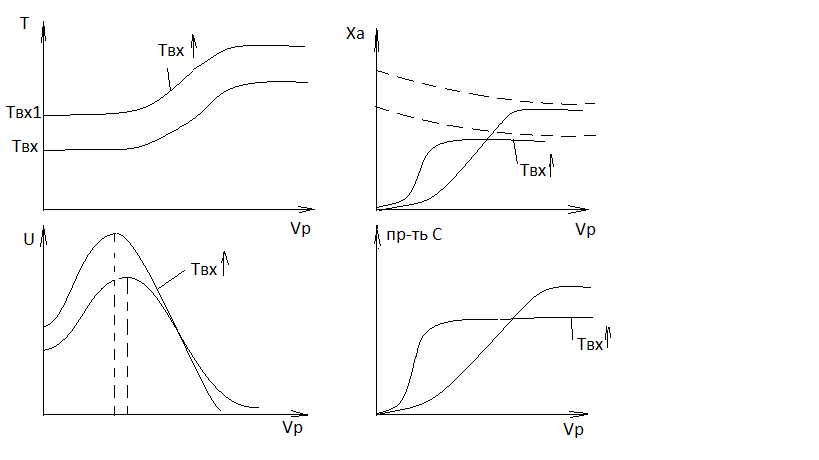
Равновесие будет смещаться в сторону исходных веществ. Скорость существенно возрастет и так же резко уменьшится. Отсюда следует, что при проведении обратимой экзотермической реакции увеличение входной температуры выгодно только в том случае если реакцию проводят вдали от равновесия. Объем реактора, при котором наблюдается пересечение Xa и U не совпадают в связи с тем, что для РИВ, в соответствии с дифференциальной формой уравнения материального баланса производная от степени превращения по объему реактора пропорциональна скорости.

С геометрической точки зрения такая производная есть касательная. В точке пересечения тангенсы угла наклона будут равны.

Для адиабатического РПС характер зависимостей при проведении процесса в адиабатическом режиме аналогичен РИВ, за исключением случая, когда в РПС наблюдается зона множественности стационарных состояний. Применительно к сравнению реакторов, работающих в адиабатическом режиме можно использовать следующую методику. Надо сравнить среднюю скорость.

Экзотермическая реакция

U РИВ UРПС

k РИВ kРПС

Д СРИВ ДСРПС

Отсюда вывод, что при проведении обратимой экзотермической реакции РПС будет предпочтительнее в том случае, если процесс проводится вдали от равновесия, РИВ будет предпочтителен если процесс проводится вблизи равновесия. Т. е. если надо обеспечить высокую температуру процесса, то использовать нужно РПС, а если надо обеспечить высокую степень превращения применяют РИВ.