
- •Вопросы по вышке
- •Матрицы и операции над ними и их свойства. Определитель матрицы порядков 2 и 3 и в общем случае.
- •Шесть основных свойств определителя 3-го порядка.
- •Определители n-го порядка (общий случай)
- •Свойства определителя матрицы и теорема о разложении.
- •Основные понятия систем линейных уравнений. Теорема Крамера.
- •Формулы Крамера
- •Основные понятия систем линейных уравнений. Метод гаусса.
- •Метод Гаусса
- •Обратная матрица. Вычисление коэффициентов, использование при решении систем линейных уравнений.
- •Компонента вектора, проекция на ось, скалярное произведение векторов на плоскости. Расстояние между точками, уравнение линии.
- •1.3.1.Преобразование компонент вектора при поворотах осей координат.
- •Уравнение прямой плоскости. Угол между прямыми и расстояние о точки до прямой на плоскости. Уравнение прямой на плоскости
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Кривые второго порядка. Уравнения эллипса, гиперболы и параболы.
- •Гипербола
- •Парабола
- •Уравнение поверхности. Уравнения плоскости и прямой в пространстве.
- •Углы между прямыми и плоскостями и расстояние от точки до плоскости.
- •Расстояние от точки до плоскости
- •Определения
- •Замечания
- •[Примеры
- •Пределы первый и второй замечательные пределы.
- •Асимптоты вертикальные, наклонные, горизонтальные, вычисление коэфицентов, графическая иллюзия.
- •Непрерывность функции в точке и на отрезке. Пределы сложной функции. Классификация точек разрыва.
- •Сложные функции
- •Классификация точек разрыва функции
- •Определение производной и дифференцируемости функции. Определение производной
- •Непрерывность дифференцируемой функции
Формулы Крамера
Метод Крамера состоит в том, что мы последовательно находим главный определитель системы (5.3), т.е. определитель матрицы А
= det (ai j)
и n вспомогательных определителей i (i= ), которые получаются из определителя заменой i-го столбца столбцом свободных членов.
Формулы Крамера имеют вид:
x i = i (i = ). (5.4)
Из (5.4) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы (5.3): если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:
x i = i / .
Если главный определитель системы и все вспомогательные определители i = 0 (i= ), то система имеет бесчисленное множество решений. Если главный определитель системы = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.
Пример 1.14. Решить методом Крамера систему уравнений:
x1 + x2 + x3 + x4 = 5, x1 + 2x2 - x3 + 4x4 = -2, 2x1 - 3x2 - x3 - 5x4 = -2, 3x1 + x2 +2x3 + 11 x4 = 0.
Решение.
Главный
определитель этой системы
=
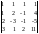 = -142
0, значит, система имеет единственное
решение. Вычислим вспомогательные
определители
i
(i=
= -142
0, значит, система имеет единственное
решение. Вычислим вспомогательные
определители
i
(i=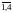 ),
получающиеся из определителя
путем замены в нем столбца, состоящего
из коэффициентов при xi,
столбцом из свободных членов:
1
=
),
получающиеся из определителя
путем замены в нем столбца, состоящего
из коэффициентов при xi,
столбцом из свободных членов:
1
=
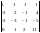 = - 142,
2
=
= - 142,
2
=
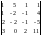 = - 284,
3
=
= - 284,
3
=
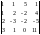 = - 426,
= - 426,
4
=
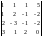 = 142. Отсюда x1
=
1/
= 1, x2
=
2/
= 2, x3
=
3/
= 3, x4
=
4/
= -1, решение системы - вектор С=(1, 2, 3, -1)T.
= 142. Отсюда x1
=
1/
= 1, x2
=
2/
= 2, x3
=
3/
= 3, x4
=
4/
= -1, решение системы - вектор С=(1, 2, 3, -1)T.
Основные понятия систем линейных уравнений. Метод гаусса.
СМОТРИ ВЫШЕ.
Метод Гаусса — Жордана (метод полного исключения неизвестных) — метод, который используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе или отыскания ранга матрицы. Метод является модификацией метода Гаусса.
Алгоритм
Выбирают первый слева столбец матрицы, в котором есть хоть одно отличное от нуля значение.
Если самое верхнее число в этом столбце есть ноль, то меняют всю первую строку матрицы с другой строкой матрицы, где в этой колонке нет нуля.
Все элементы первой строки делят на верхний элемент выбранного столбца.
Из оставшихся строк вычитают первую строку, умноженную на первый элемент соответствующей строки, с целью получить первым элементом каждой строки (кроме первой) ноль.
Далее проводят такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.
После повторения этой процедуры
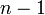 раз
получают верхнюю
треугольную матрицу
раз
получают верхнюю
треугольную матрицуВычитаем из предпоследней строки последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в предпоследней строке осталась только 1 на главной диагонали.
Повторяют предыдущий шаг для последующих строк. В итоге получают единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования).
Чтобы получить обратную матрицу, нужно применить все операции в том же порядке к единичной матрице.
