Описание
Нормальные алгорифмы являются вербальными, то есть предназначенными для применения к словам в различных алфавитах.
Определение
всякого нормального алгорифма состоит
из двух частей: определения алфавита алгорифма
(к словам из символов которого алгорифм
будет применяться) и определения
его схемы.
Схемой нормального алгорифма называется
конечный упорядоченный набор так
называемых формул
подстановки,
каждая из которых может
быть простой илизаключительной.
Простыми формулами подстановки называются
слова вида 
,
где 
и 
—
два произвольных слова в алфавите
алгорифма (называемые, соответственно,
левой и правой частями формулы
подстановки). Аналогично, заключительными
формулами подстановки называются слова
вида 
,
где
и
—
два произвольных слова в алфавите
алгорифма. При этом предполагается, что
вспомогательные буквы 
и 
не
принадлежат алфавиту алгорифма (в
противном случае на исполняемую ими
роль разделителя левой и правой частей
следует избрать другие две буквы).
Примером
схемы нормального алгорифма в пятибуквенном
алфавите 
может
служить схема
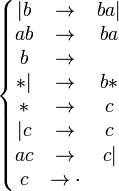
Процесс
применения нормального алгорифма к
произвольному слову
в
алфавите этого алгорифма представляет
собой дискретную последовательность
элементарных шагов, состоящих в следующем.
Пусть 
—
слово, полученное на предыдущем шаге
работы алгорифма (или исходное слово
,
если текущий шаг является первым). Если
среди формул подстановки нет такой,
левая часть которой входила бы в
,
то работа алгорифма считается завершённой,
и результатом этой работы считается
слово
.
Иначе среди формул подстановки, левая
часть которых входит в
,
выбирается самая первая. Если эта формула
подстановки имеет вид
,
то из всех возможных представлений
слова
в
виде
выбирается
такое, при котором 
—
самое короткое, после чего работа
алгорифма считается завершённой с
результатом 
.
Если же эта формула подстановки имеет
вид
,
то из всех возможных представлений
слова
в
виде
выбирается
такое, при котором
—
самое короткое, после чего слово
считается
результатом текущего шага, подлежащим
дальнейшей переработке на следующем
шаге.
Например,
в ходе процесса применения алгорифма
с указанной выше схемой к
слову 
последовательно
возникают слова 
, 
, 
, 
, 
, 
, 
, 
, 
, 
и 
,
после чего алгорифм завершает работу
с результатом 
.
Другие примеры смотрите ниже.
Любой нормальный алгорифм эквивалентен некоторой машине Тьюринга, и наоборот — любая машина Тьюринга эквивалентна некоторому нормальному алгорифму. Вариант тезиса Чёрча — Тьюринга, сформулированный применительно к нормальным алгорифмам, принято называть «принципом нормализации».
Нормальные алгорифмы оказались удобным средством для построения многих разделов конструктивной математики. Кроме того, заложенные в определении нормального алгорифма идеи используются в ряде ориентированных на обработку символьной информации языков программирования — например, в языке Рефал.
-------39 Машины Тьюринга
Маши́на Тью́ринга (МТ) — абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 годудля формализации понятия алгоритма.
Машина Тьюринга является расширением конечного автомата и, согласно тезису Чёрча — Тьюринга, способна имитировать все другие исполнители (с помощью задания правил перехода), каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.