
- •Абсолютное и относительное движения точки. Переносное движение. Теорема о сложении скоростей.
- •Сложение ускорений. Теорема Кореолиса.
- •Мгновенный центр скоростей. Определение ускорения любой точки фигуры как геометрической суммы ускорения полюса и ускорения этой точки при вращении фигуры вокруг полюса.
- •Сферическое движение твердого тела. Теорема Эйлера-Даламбера. Мгновенная ось вращения тела. Векторы угловой скорости и углового ускорения тела.
- •Cкорости и ускорения точек твердого тела, имеющего одну неподвижную точку.
- •Основные аксиомы статики. Связи. Реакции связей.
- •2. Система сходящихся сил. Теорема о трех силах.
- •3. Плоская система сил. Теорема Вариньона о равнодействующей. Свойства момента сил относительно центра.
- •4. Пара сил на плоскости. Теорема об эквивалентности пар сил на плоскости.
- •Условия равновесия плоской системы сил. Лемма Пуансо. Привидение плоской системы сил к простейшим системам.
- •Пространственная система сил. Лемма Пуансо. Свойства векторного момента сил относительно центра. Пара сил в пространстве. Момент силы относительно оси
- •Условия равновесия пространственной системы сил. Приведение пространственной системы сил к простейшим системам. Силовая динама.
Кинематика – раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.
Понятия скорости и ускорения точки. Подсчет скорости и ускорения при координатном способе задания движения. Касательное и нормальное ускорение точки.
Скорость – ВФВ, хар. изменение перемещение за единицу времени
Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую средней по модулю и направлению скоростью точки за промежуток времени (при криволинейном движении направлено в сторону движения точки, а прямолинейном – вдоль самой траектории) Vср=ММ1/t=∆ r/∆ t=dr/dt
Скоростью точки в данный момент времени называется ВФВ V, к которой стремится средняя скорость Vср при стремлении промежутка времени к нулю (равна первой производной от радиуса - вектора точки по времени, направлен по касательной к траектории точки в сторону движения)
Ускорение – ВФВ, хар. изменение вектора скорости за единицу времени.
Отношение приращения
вектора скорости к соответствующему
промежутку времени определяется вектором
среднего ускорения точки
за этот промежуток времени аср=
∆V/∆t
(вектор ускорения имеет тоже направление
как и ∆V,
в сторону вогнутости траектории; = первой
производной от вектора скорости или
второй от перемещения)
![]()
Ускорением точки в данный момент времени называется векторная величина, к которой стремится среднее ускорение при стремлении промежутка времени к нулю
а=lim ∆V/∆t= dV/dt
при прямолинейном движении вектор а направлен вдоль прямой, по которой движется точка. Если плоская кривая , то в сторону вогнутости как вектор среднего ускорения
Способы описания движения м.т.: векторный, координатный, траекторный.
Координатный способ задания движения точек.
f=f(x;у;z;t) x=x(t),y=y(t),z=z(t); r=xi+yj+zk; r2=x2+y2+z2
Положение точки можно непосредственно определять ее декартовыми координатами x,y,z, которые при движении точки будут, с течением времени, изменятся.
x=x(t),y=y(t),z=z(t); эти уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах
Определение скорости из V=dr/dt, Vx=x’, Vy=y’, Vz=z’, Таким образом, проекции скорости точки на координатную оси равны первым производным от соответствующих координат точки по времени.
Затем, зная проекции
скорости, найдем ее модуль и направление
и углы, которые вектор V
образует с координатными осями.

Определение ускорения из а=dV/dt, ax=x’’, ay=y’’, az=z’’, т.е.проекции ускорения точки на координатные оси равны первым производным от проекции скорости или вторым производным от соответствующих координат точки по времени
Модуль и направление
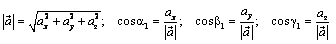 – углы, образуемые вектором ускорения
с координатными осями.
– углы, образуемые вектором ускорения
с координатными осями.
В случае прямолинейного движения, которое задается одним уравнением x=f(t), будет Vx=dx/dt; ax=dVx/dt=d2x/dt2
Касательное и нормальное ускорения точки.
Проектируя на ось тау и n, мы получаем aтан=(dV)тан/dt; an=(dV)n/dt
aтан=(dV) /dt; an=Vd фир/dt=V2/Ро, где фир- угол смежности – элементарный угол смежности; Ро-радиус кривизны траектории
aтан=dV/dt=d2S/dt2; an=V2/ро=Vw; ab=0
![]()
Косательное всегда направлено по косательной к траектории, а нормальное в сторону вогнутости кривой, центру окружности, т.к. всегда больше 0.
Абсолютное и относительное движения точки. Переносное движение. Теорема о сложении скоростей.
Движение, которое относится сразу к двум системам отсчета, одна из которых является основной, а другая, определенным образом движется по отношению к первой, называют сложным или составным. Таким образом, сложное движение рассматривается на два простых.
Движение, совершаемое м.т. по отношению к подвижной системе отсчета, называется относительным движением.
Траектория, описываемая точкой, называется относительной траекторией. Скорость, по отношению к осям Оxyz называется относительной скоростью, ускорение - относительным ускорением. Из определения следует, что при вычислении скорости и ускорения можно движение осей Оxyz во внимание не принимать (рассматривать как неподвижные)
Движение, совершаемое подвижной системой отсчета Оxyz по отношению к неподвижной системой О1x1y1z1 является для м.т. переносным движением.
Скорость той неизменной связанной с подвижным осями Оxyz м.т(малое)., с которой в данный момент времени совпадает движущаяся м.т., называется переносной скоростью т.М в этот момент, а ускорение м.т.(малое) – переносным ускорением м.т.
Движение, совершаемое точкой по отношению к неподвижной системе отсчета О1x1y1z1 называется абсолютным или сложным. Траектория этого движения называется абсолютной, скорость и ускорения – абсолютная …
Пример: движение шара относительно палубы, будет относительный, движение парохода относительно берега будет переносным, движение шара, относительно к берегу, будет абсолютным.
Теорема о сложении скоростей.
При сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей. Vаб=Vот+Vпер
Если угол между векторами Vот и Vпер. Равен альфа, то по модулю Vаб2= Vот2+Vпер2+2VОтVперcosальфа
Сложение ускорений. Теорема Кореолиса.
При сложном движении ускорение точки равно геометрической сумме трех ускорений: относительного, переносного и поворотного (кореолисова). ааб=аот+апер+акор
акор =2(w*Vот) =2|w|*|Vот|sin альфа. Кореолисово ускорение равно удвоенному векторному произведению переносной угловой скорости на относительную скорость точки.
В случае поступательного переносного движения w=0, следовательно акор=0,следовательно ааб=аот+апер
ааб можно найти методом проекции на оси x, y, z
Кореолисово ускорение может быть равно нулю
когда w=0, т.е. когда переносное движение является поступательным или есть переносная угловая скорость в данный момент времени обращается в нуль;
когда Vотн =0, т.е. относительная скорость в данный момент времени обращается в нуль.
Когда альфа=0=180, т.е. когда относительное движение происходит по направлению, параллельному оси переносного вращения, или если в данный момент времени вектор Vотн параллелен этой оси.
Правило Жуковского.
Находим проекцию вектора относительной скорости на плоскость, перпендикулярную оси, а затем эту проекцию повернуть на 90 в сторону вращения. Если движение лежит в одной плоскости, перпендикулярной оси, то нужно повернуть вектор относительной скорости на 90 в сторону вращения
Поступательное и вращательное движение твердого тела. Вектор угловой скорости и углового ускорения.
Задачи кинематики твердого тела распадаются на две части: 1) задание движения и определение кинематических характеристик движения тела в целом; 2) определение кинематических характеристик движения отдельных точек тела.
Поступательным называется такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельной своему начальному направлению.
Свойства поступательного движения определяются теоремой: при поступательном движении все точки тела описывают одинаковые (при наложении совпадающие) траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения.
Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижным. Проходящая через неподвижные точки прямая называется осью вращения. Положение тела в любой момент времени однозначно определится взятым с соответствующим знаком углом ФИР между этими полуосями, который называется углом поворота тела. Измеряется в радианах. Уравнение фир=f(t) выражает закон вращательного движения твердого тела вокруг неподвижной оси.
Фир=w’=E’’
Угловое ускорение характеризует изменение с течением времени угловой скорости тела.
Числовое значение угловой скорости тела в данный момент времени равно первой производной от угла поворота по времени.
Числовое значение углового ускорения тела в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота тела по времени.
Если модуль угловой скорости со временем возрастает, вращение тела называется ускоренным, а если убывает – замедленным (вращение будет ускоренным, когда величины w и E будут иметь одинаковые знаки, и замедленным когда разные; направление E совпадает с направлением w, когда тело вращается ускоренно, и противоположно w при замедленном вращении)
5. Плоское движение твердого тела. Разложение движения плоской фигуры на поступательное вместе с полюсом и вращательное вокруг полюса. Независимость угловой скорости и углового ускорения фигуры от выбора полюса.
Плоскопараллельным (или плоским) называется такое движение твердого тела, при котором все его точки перемещаются параллельно некоторой фиксированной плоскости. Рассматривается сечение фигуры.
Уравнение xa=f1(t), ya=f2(t)- при фир=const; фир=f3(t)-при ха и уа = сonst, определяющие закон происходящего движения, называются уравнениями движения плоской фигуры в ее плоскости. Они же являются уравнениями плоскопараллельного движения твердого тела. В общем случае движение плоской фигуры в ее плоскости может рассматриваться как слагающееся из поступательного движения, при котором все точки фигуры движутся так же, как полюс 1, и из вращательного движения вокруг этого полюса.
При изучении движения можно в качестве полюса выбирать любую точку фигуры. Если вместо 1го полюса взять 2ой и определять ее положение. Характеристики поступательной части движения при этом изменятся, так как в общем случае вектора Vc(ac) не равно Va(aa) (иначе бы движение фигуры было поступательным). Характеристики вращательного части движения остаются неизменными.
Вращательная часть движения от выбора полюса не зависит.
