
- •Факторы, влияющие на частоту собственных колебаний лопатки
- •Определение частоты колебания лопатки в поле центробежных сил
- •4. Резонансные режимы и способы борьбы с опасными колебаниями
- •Силы, демпфирующие колебания
- •14. Критические скорости вращения реальных роторов
- •17. Расчет крических скоростей вращения многодисковых роторов
- •12. Вынуждающие моменты и резонанс
Факторы, влияющие на частоту собственных колебаний лопатки
Проведём анализ зависимости (2.54).
При увеличении длины лопатки собственная частота первой формы колебаний уменьшается пропорционально квадрату отношения длин лопаток:
 .
.
Изменение температуры лопатки изменяет
модуль упругости материала
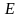 .
Повышение температуры снижает Е и,
следовательно, частоту собственных
колебаний лопатки по соотношению
.
Повышение температуры снижает Е и,
следовательно, частоту собственных
колебаний лопатки по соотношению
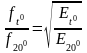 .
.
Материал лопатки характеризуется
отношением
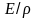 .
Для материалов, из которых изготавливаются
лопатки, это отношение меняется
незначительно. Так частоты собственных
колебаний стальных лопаток всего на
5…7% , а титановых на 6…8% больше чем
изготовленной из алюминия при тех же
размерах. Однако усталостная прочность
у лопаток из алюминия ниже в 4…5 раз.
.
Для материалов, из которых изготавливаются
лопатки, это отношение меняется
незначительно. Так частоты собственных
колебаний стальных лопаток всего на
5…7% , а титановых на 6…8% больше чем
изготовленной из алюминия при тех же
размерах. Однако усталостная прочность
у лопаток из алюминия ниже в 4…5 раз.
Уменьшение осевых моментов инерции
сечения лопатки
 приводит
к снижению первой собственной частоты
колебаний лопатки пропорционально
корню квадратному из отношения моментов
приводит
к снижению первой собственной частоты
колебаний лопатки пропорционально
корню квадратному из отношения моментов

Также на частоту колебаний существенно влияют параметры профиля – толщина, клиновидность, трапециевидность, закрученность.
Так, увеличение толщины профиля, в большей степени увеличивает жёсткость, чем массу, поэтому частота собственных колебаний также увеличивается.
Увеличение клиновидности (уменьшение
отношения
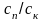 ),
при неизменной площади корневого
сечения, повышает частоту первой формы
изгибных колебаний.
),
при неизменной площади корневого
сечения, повышает частоту первой формы
изгибных колебаний.
Уменьшение трапециевидности (отношение
длины хорды лопатки на периферии к длине
хорды в корневом сечении
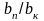 ),
при постоянной площади корневого
сечения, приводит к снижению частоты
собственных колебаний лопатки.
),
при постоянной площади корневого
сечения, приводит к снижению частоты
собственных колебаний лопатки.
Закрутка лопатки большого влияния на частоту колебаний не оказывает.
На частоту собственных колебаний лопатки оказывает влияние форма перехода от пера к хвостовику, тип и форма хвостовика, а также усилие затяжки хвостовика в диске.
Определение частоты колебания лопатки в поле центробежных сил
При вращении ротора на лопатку действует центробежная сила, которая повышает частоту собственных колебаний. Центробежная сила стремится выпрямить ось лопатки, отклоняющуюся при колебаниях.
Центробежная сила приводит к повышению жёсткости лопатки, как натяжение струны в музыкальных инструментах. Влияние центробежной силы возрастает с увеличением закрутки лопатки, угла установки. Бандажная полка также повышает влияние центробежной силы на увеличение собственной частоты колебаний.
Кроме того, в конструкциях, где хвостовик лопатки устанавливается свободно в диске, центробежная сила увеличивает защемление хвостовика лопатки и тем самым повышает частоту собственных колебаний.
Определение частоты колебаний лопатки в поле центробежных сил проведем энергетическим методом. Рассмотрим колебание лопаток с жесткой заделкой в ободе диска в плоскости наименьшей жесткости.
Лопатку представим как упругую невесомую
балку с приведенной массой на конце
(рис.2.8). К массе приложена центробежная
сила
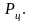
При свободных колебаниях сумма
потенциальной
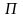 и
кинетической
и
кинетической
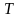 энергий
должна оставаться постоянной
энергий
должна оставаться постоянной
 (2.56)
(2.56)
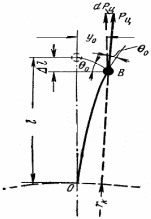
Рис.2.8. К расчету частоты
колебаний лопатки в поле
центробежных сил
В процессе колебаний приведенная масса
на упругой балке отклонится на угол
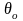 ,
при этом центробежная сила совершает
работу. Пренебрегаем ввиду малости
окружной составляющей центробежной
силы
,
при этом центробежная сила совершает
работу. Пренебрегаем ввиду малости
окружной составляющей центробежной
силы
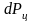 ,
получим максимальную работу центробежных
сил при максимальном прогибе
,
получим максимальную работу центробежных
сил при максимальном прогибе
 (2.57)
(2.57)
где, ввиду малости
можно принять
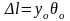 ,
а
,
а
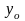 ,
-
максимальный прогиб и угол наклона
лопатки.
,
-
максимальный прогиб и угол наклона
лопатки.
Примем, что форма упругой линии лопатки близка к форме упругой линии балки, нагруженной сосредоточенной на конце силой Р, то потенциальная энергия деформации стержня будет равна этой работе
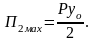 (2.58)
(2.58)
Прогиб
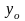 от силы Р определится
от силы Р определится
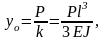 (2.59)
(2.59)
где
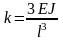 - коэффициент жесткости.
- коэффициент жесткости.
Подставим значения
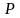 из равенства (2.59)в зависимость (2.58),
получим
из равенства (2.59)в зависимость (2.58),
получим
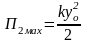 .
(2.60)
.
(2.60)
Кинетическая энергия соответствующая максимальной скорости, равна
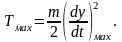 (2.61)
(2.61)
При колебаниях масса перемешается по гармоническому закону
 (2.62)
(2.62)
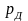 -
круговая частота лопатки, находящейся
в поле центробежных сил.
-
круговая частота лопатки, находящейся
в поле центробежных сил.
Дифференцируя уравнения (2.62), получим
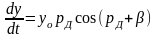 (2.63)
(2.63)
Подставим (2.63) в (2.61) получим зависимость
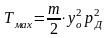 (2.64)
(2.64)
Подставляем полученные выражения для потенциальной и кинетической энергии в (2.56), получим
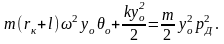 (2.65)
откуда
(2.65)
откуда
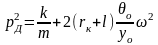 (2.66)
(2.66)
Подставим в (2.66) зависимости для прогиба (2.59) и угла наклона от силы Р
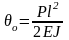 и учитывая, что
и учитывая, что
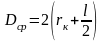
получим
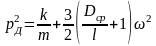 (2.67)
(2.67)
Обозначим
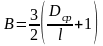 ,
,
тогда (2.67) запишется
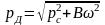 , (2.68)
, (2.68)
где
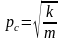 круговая частота колебаний неподвижной
лопатки
круговая частота колебаний неподвижной
лопатки
Линейные частоты связаны с круговыми соотношениями
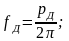
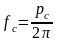
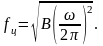
Частота собственных колебаний лопатки
с учётом центробежной силы
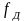 определяется
частотой собственных колебаний при
неподвижном роторе
определяется
частотой собственных колебаний при
неподвижном роторе
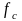 и
частоты колебаний идеально гибкой
лопатки находящейся в поле центробежных
сил
и
частоты колебаний идеально гибкой
лопатки находящейся в поле центробежных
сил
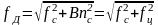 (2.69)
(2.69)
Расчёт частот собственных колебаний лопатки с учётом всех факторов сложен, поэтому рассмотрим полуэмпирические зависимости.
Для расчёта первой собственной частоты колебаний лопатки коэффициент В определяется:
- лопатка с постоянным по длине сечением
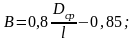
- лопатка с переменным по длине сечением
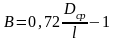
- лопатка закрученная, переменного сечения
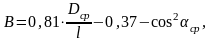
где
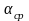 -
средний по длине угол закрутки лопатки,
-
средний по длине угол закрутки лопатки,
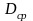 -
средний радиус лопатки;
-
средний радиус лопатки;
 -
длина лопатки.
-
длина лопатки.
