
- •1.Анализ и синтез изображений, растровая и векторная графика. Компьютерная и инженерная графика как наука и индустрия. Основные понятия и определения.
- •3.История, устройство и работа видеоадаптеров, современные 3d графические процессоры Современные тенденции конструирования видеоадаптеров.
- •4. Растровые алгоритмы компьютерной графики. Антиалисинг, сглаживание, дизеринг. Алгоритмы рисования окружности и отрезка. Инкрементный алгоритм Брезенхема. Алгоритмы закрашивания.
- •Параметрическое задание кривых на плоскости и в пространстве. Кривые Безье.
- •Кривая Безье (Bezier curve).
- •Виды сплайнов, применяемых в компьютерной графике.
- •6.Форматы графических файлов: растровые и векторные, сферы их применения. Структура форматов bmp, gif, jpeg. Алгоритмы кодирования информации: rle, lzw, по Хаффману. Сжатие с потерями.
- •Где матрица преобразований m имеет следующий вид:
- •1.Способы проецирования в инженерной графике. Проецирование на плоскость. Параллельные проекции, их классификация и применение. Перспективная проекция.
- •3. Форматы, типы линий, масштабы, шрифты, штриховки – стандарты.
- •1) Вынесенные 2) наложенные.
- •8. Зубчатые колёса, зубчатые и цепные передачи, шлицевые и шпоночные соединения: обозначение на чертежах.
Параметрическое задание кривых на плоскости и в пространстве. Кривые Безье.
Параметрически
заданной кривой называется
множество точек M(x,y,z), координаты которых
определяются соотношениями x
= x(t),
y
= y(t),
z
= z(t),
![]() .
В векторной форме
.
В векторной форме
![]() .
.
Кривая
называется регулярной,
если
![]() в каждой её точке; т.е. в каждой точке
кривой существует касательная, положение
которой меняется непрерывно вдоль
кривой.
в каждой её точке; т.е. в каждой точке
кривой существует касательная, положение
которой меняется непрерывно вдоль
кривой.
Геометрическим образом функции трех переменных F(x,y,z) служит поверхность. Чтобы определить положение точки на ней, нужны два параметра U и V (например, широта и долгота на поверхности шара).
Кривая Безье (Bezier curve).
Алгоритм независимо получен Пьером Безье и Полем Кастельё в конце 60-х годов для технического проектирования. Применяется в интерактивных системах компьютерной графики для приближенного решения задач на построение кривых по точкам.
Пусть
на плоскости или в пространстве задан
набор точек-ориентиров
![]() .
Кривой Безье, определяемой этим набором
точек, называется кривая, определяемая
уравнением
.
Кривой Безье, определяемой этим набором
точек, называется кривая, определяемая
уравнением
![]() ,
,
где
,
,
где
![]() – число сочетаний из n
элементов по i
(коэффициент в разложении бинома
Ньютона).
– число сочетаний из n
элементов по i
(коэффициент в разложении бинома
Ньютона).
Элементарная
кубическая кривая Безье для четырёх
точек-ориентиров
![]() задаётся параметрическим уравнением:
задаётся параметрическим уравнением:
![]() ,
,
(IV.15)
,
,
(IV.15)
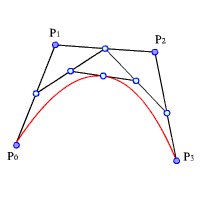
или в матричной записи4:
рис.
IV.10. Способ
вычерчивания
куб. кривой Безье![]() ,
(IV.16)
,
(IV.16)
V2
V1
рис.
IV.11
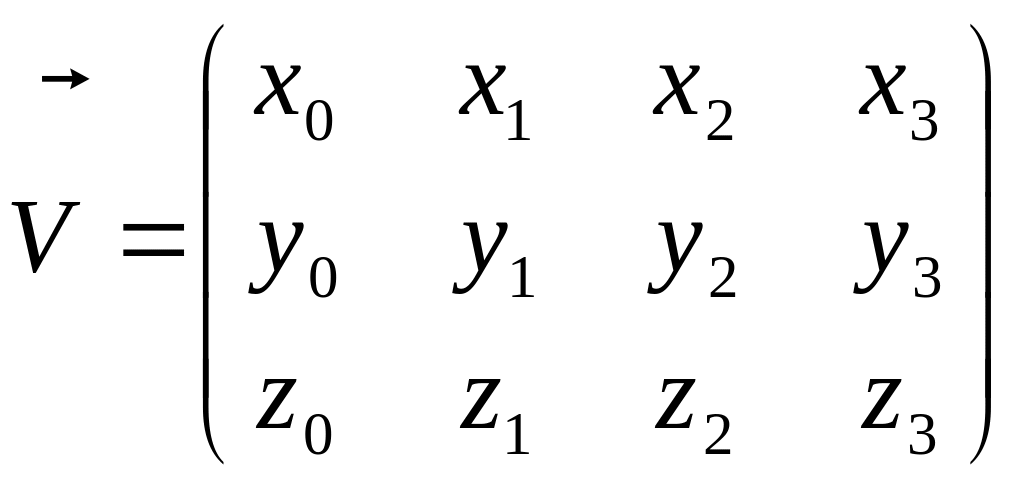 ,
,
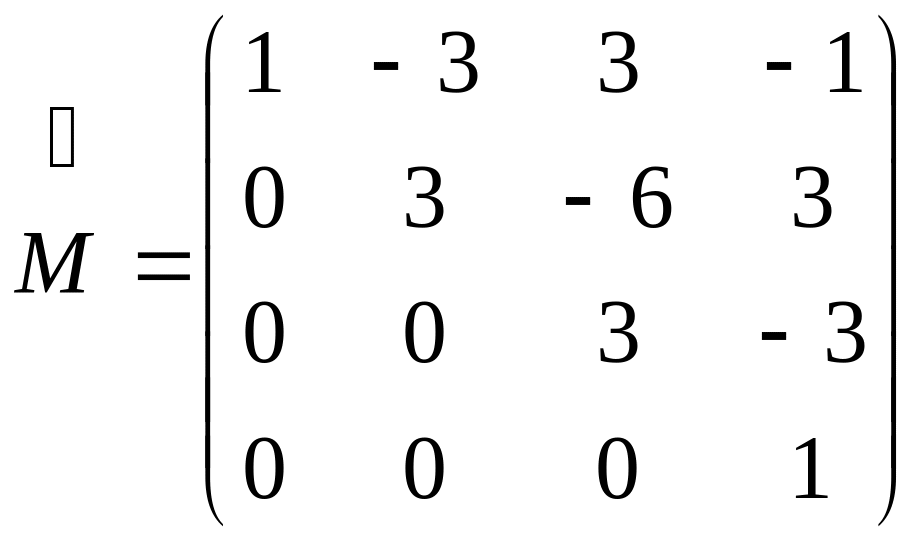 ,
,
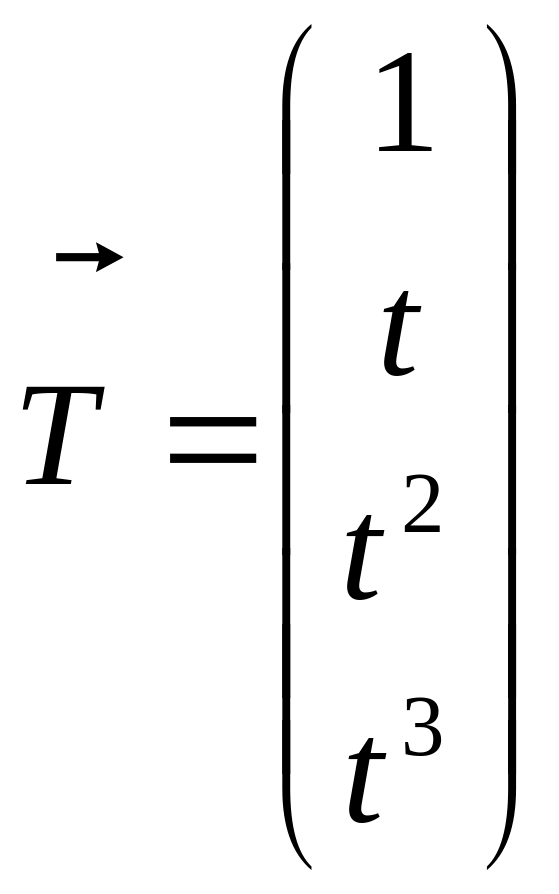 . (IV.17)
. (IV.17)
P1
P2![]()
Свойства кривой Безье:
Является гладкой;
Начинается
точно в точке
![]() и заканчивается в
и заканчивается в
![]() ,
касаясь при этом отрезков
,
касаясь при этом отрезков
![]() и
и
![]() ;
;
Целиком лежит в выпуклой оболочке, порождаемой массивом точек-ориентиров (рис. IV.11 даёт представление, как создаётся элементарная кривая Безье в программе Adobe Illustrator между двумя точками и двумя их подвижными направляющими – handles);
Степень функциональных коэффициентов напрямую связана с количеством точек в наборе; при добавлении хотя бы одной новой точки надо пересчитать все коэффициенты; изменение координат одной точки приводит к заметному изменению вида всей кривой;
Многочлен
Безье можно представить как некоторую
намагниченную эластичную ленту,
закреплённую в точках
![]() ;
точки-ориентиры представляются магнитами,
к которым притягивается эта лента.
Несколько точек-ориентиров могут иметь
одинаковые координаты, при этом
увеличивается вес
такой точки, т.е. кривая притягивается
ближе к ней.
;
точки-ориентиры представляются магнитами,
к которым притягивается эта лента.
Несколько точек-ориентиров могут иметь
одинаковые координаты, при этом
увеличивается вес
такой точки, т.е. кривая притягивается
ближе к ней.
В
практических вычислениях часто
оказывается удобным пользоваться
кривыми, составленными из элементарных
кривых Безье. Определим составную
кубическую кривую Безье как объединение
элементарных кубических кривых Безье,
так что
![]() .
.
Виды сплайнов, применяемых в компьютерной графике.
Сплайн (spline). Термин произошёл от названия гибкой полоски стали, при помощи которой чертёжники проводили через заданные точки плавные кривые. Математическое описание –Шенберг, 1946. Суть: задают координаты небольшого числа опорных точек, через них строят плавные кривые или поверхности.
Рассмотрим
представление кривой в декартовых
координатах на плоскости. Пусть задан
набор точек
![]() ,
i
= 0,1…n.
Интерполяционным
составным кубическим сплайном
называется функция S(x),
обладающая следующими свойствами:
,
i
= 0,1…n.
Интерполяционным
составным кубическим сплайном
называется функция S(x),
обладающая следующими свойствами:
график функции проходит через каждую точку из заданного набора, т.е. S(xi) = yi;
на каждом из отрезков [xi, xi+1], i = 0,1…n-1 функция
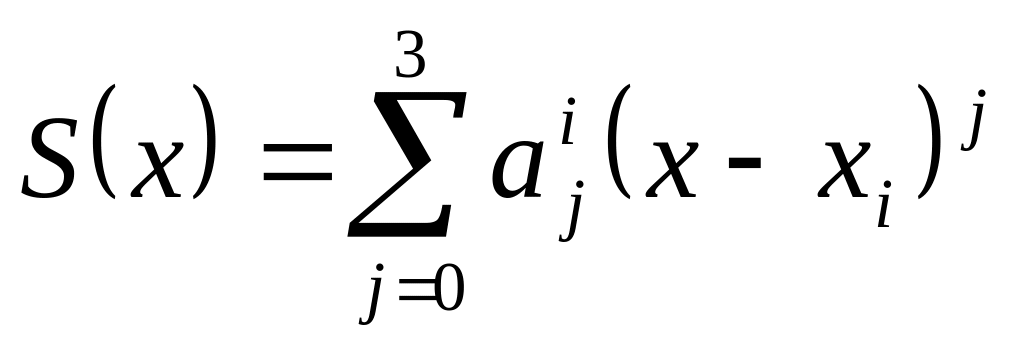 является многочленом третьей степени.
является многочленом третьей степени.На всём отрезке [x0, xn] функция имеет непрерывными первую и вторую производную.
Так как на каждом из отрезков [xi, xi+1] сплайн S(x) определяется четырьмя коэффициентами, то для его полного описания на всей области задания необходимо найти 4n коэффициентов. Учёт трёх вышеперечисленных условий даёт систему из 4n-2 линейных алгебраических уравнений, оставшиеся два граничных условия задаются специально, например так: S /(x0) = l0, S /(xn) = l1.5
Для продолжения описания сплайнов различных видов, используемых в компьютерной графике, вновь вернёмся к параметрическому описанию кривых (в котором, например, очень легко рассматривать кривую, пересекающую саму себя, рис. IV.11).
B-сплайн
(basic spline)
- кусочно-полиномиальная функция. Можно
построить этот сплайн по четырём заданным
точкам
![]() .
При этом элементарная кубическая
B-сплайновая
кривая определяется векторным
параметрическим уравнением:
.
При этом элементарная кубическая
B-сплайновая
кривая определяется векторным
параметрическим уравнением:
![]() ,
,
(IV.18)
,
,
(IV.18)
или в матричной форме:
,
где
 ,
,
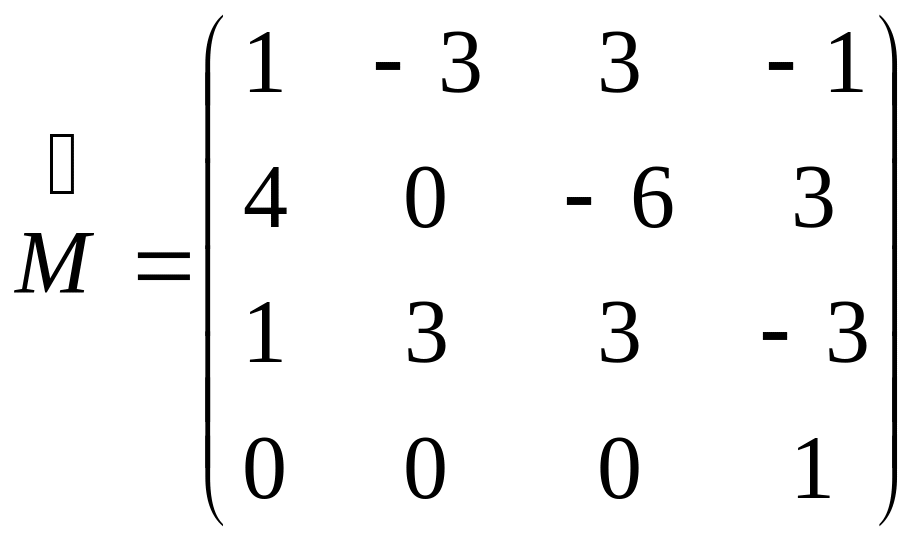 ,
,
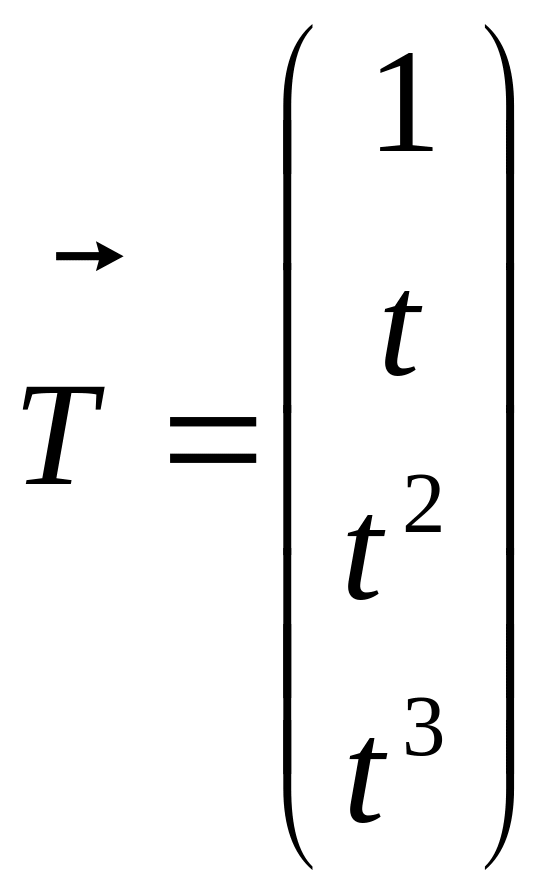
П
С
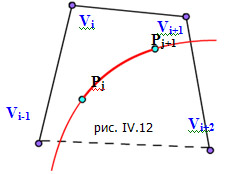
Vi-1![]() представляет собой объединение n-2
элементарных кубических B-сплайновых
кривых, каждая из которых описывается
уравнением
представляет собой объединение n-2
элементарных кубических B-сплайновых
кривых, каждая из которых описывается
уравнением
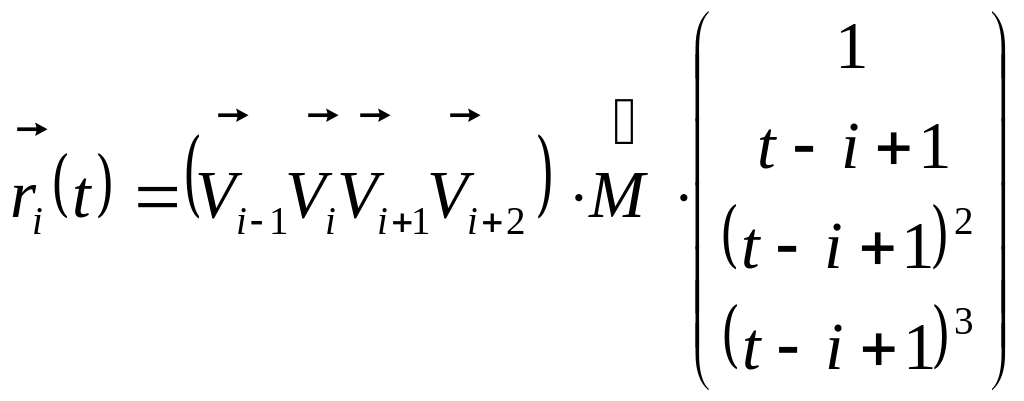 ,
,
![]() ,
,
![]() ,
(IV.20)
,
(IV.20)
т.е. кривая строится между двумя точками на основе информации о координатах двух соседних с ними. Полученная кривая имеет непрерывную вторую производную. Удобно, что коэффициенты вычисляются только один раз для каждого сегмента кривой. Представленный способ изменения t называют параметризацией с равноотстоящими целочисленными узлами.
Рациональные B-сплайны – содержат весовые коэффициенты, с помощью которых можно быстро “подправить” уравнение B-сплайновой кривой, не изменяя исходного массива точек. Кривизна этих объектов определяется положением контрольных точек, а положение любой точки поверхности вычисляется по математическим формулам (отсюда и слово «rational»).
По заданному набору точек элементарная рациональная кубическая B-сплайновая кривая определяется уравнением:
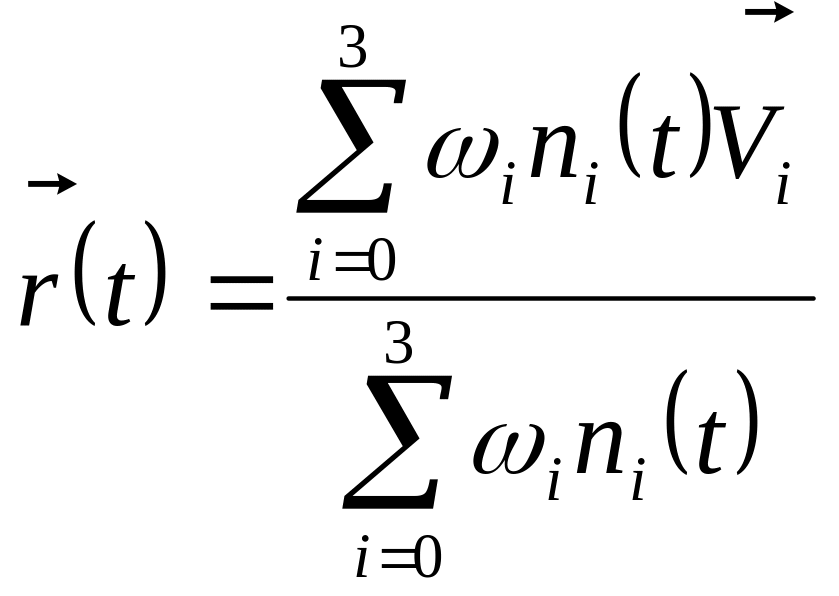 ,
,
где (IV.21)
,
,
где (IV.21)
![]() ,
,
![]() ,
,
![]() ,
,
![]() , (IV.22)
, (IV.22)
а величины ωi – веса (параметры формы) для каждой точки, величины >0. Если веса равны между собой – случай кубической B-сплайновой кривой. Составная кривая строится также как в случае B-сплайна.
NURBS (nonuniform rational B-spline) – рациональные B-сплайны, заданные на неравномерной сетке по параметру t (отсюда термин “non-uniform” – «неоднородный»). Основные свойства: просты в описании, инвариантны относительно масштабирования, сдвига, вращения и перемещения. Для управления NURBS-объектами используются специальные точки, именуемые контрольными узлами. Все контрольные узлы NURBS-кривой находятся во взаимосвязи, воспринимают перемещения окружающих узлов и занимают таким образом новое положение, обеспечивающее цельность и гладкость поверхности.
Изменяя для NURBS-поверхности положение контрольных узлов и их вес (степень влияния) в процессе анимации легко достигать эффектов, характерных для ткани или кожного покрова животных или иных органических поверхностей.
β-сплайн (Beta-spline) – кривая, построенная на основе однородного кубического B-сплайна, имеющая дополнительные параметры для учета локального наклона и гладкости.
Пусть
имеем две элементарные кривые, заданные
параметрическими уравнениями
![]() и
и
![]() .
Для получения составной регулярной
кривой потребуем совпадения в общей
точке единичных касательных векторов
и векторов кривизны. Это будет возможно
если:
.
Для получения составной регулярной
кривой потребуем совпадения в общей
точке единичных касательных векторов
и векторов кривизны. Это будет возможно
если:
![]() ,
,
![]() ,
,
![]() , (IV.23)
, (IV.23)
где
β1,
β2
– числовые параметры >0. При этом
уравнение элементарной кубической
β-сплайновой
кривой, порожденной наборами точек
![]() выглядит в матричном виде так:
выглядит в матричном виде так:
, где (IV.24)
![]() ,
,
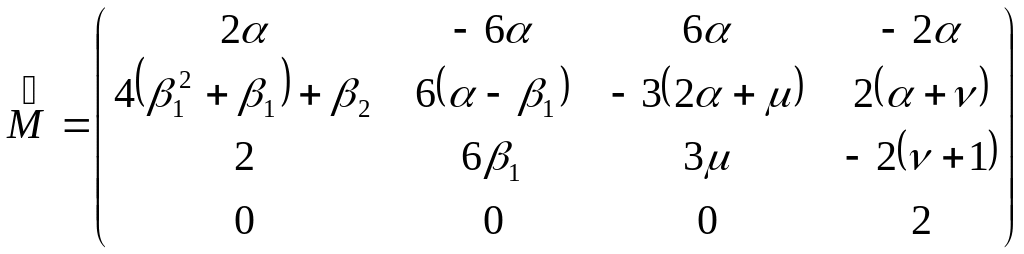 ,
,
при
этом
![]() ,
,
![]() ,
,
![]() .
Параметр β1
носит название параметр
скоса,
β2
–
параметр
натяжения.
Эти параметры влияют на форму всей
кривой. Если β1=1,
β2=0,
то мы получим кубическую В-сплайновую
кривую.
.
Параметр β1
носит название параметр
скоса,
β2
–
параметр
натяжения.
Эти параметры влияют на форму всей
кривой. Если β1=1,
β2=0,
то мы получим кубическую В-сплайновую
кривую.
Определение фрактала, данное Мандельбротом, звучит так: "Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому". Т.е. одним из основных свойств фракталов является самоподобие. В самом простом случае небольшая часть фрактала содержит информацию о всей кривой.
