22. Полная и локальная производные вектора. Формула Бура.

Рассмотрим изменение вектора b(t) по отношению к двум системам координат — подвижной O'XYZ и неподвижной Oxyz.

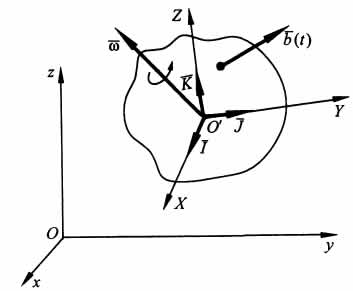
Абсолютной, или полной, производной вектора b по аргументу t назьшается вектор   определяющий изменение вектоpa b(t) в неподвижной системе Oxyz.

Относительная, или локальная, производная  определяет измененине вектора b(t) в подвижной системе O'XYZ.

Формула Бура (получается из зависимости между полной и локальной производными):  .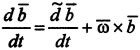

Рассомтрим частные случаи.

1) угловая скорость = 0, то  = ;

2) вектор b не меняется в подвижной системе отсчета ( =0), то  ;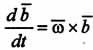

3)  , т.е. вектор b все время параллелен вектору угловой скорости ( ), то  = . В частности, если  , то  , т.е. вектор угловой скорости изменяется одинаково для подвижной и неподвижной систем координат.

Дополнение:

Выведение формулы Бура:

Найдем зависимость между полной и локальными производными. Если воспользоваться проекциями вектора b(t) на оси подвижной системы O'XYZ, то можно записать: , где I, J, К — орты, не изменяемые в этой системе отсчета. Поэтому локальная производная  , а полная производная   с учетом изменения также ортов I, J , К имеет вид: 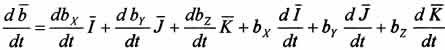 . В правой части уравнения первые три слагаемых выражают локальную производную, а производные от ортов I, J, K определяются формулами Пуассона ( ), т.е.  . С учетом   получаем:  .

23. Скорости и ускорения точки при сложном движении.

Основные задачи кинематики сложного движения заключаются в установлении зависимостей между кинематическими характеристиками абсолютного и относительного движений точки (или тела) и характеристиками движения подвижной системы отсчета, то есть переносного движения. Для точки эти зависимости являются следующими: абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей, то есть:

или

.

Связь ускорений можно найти путём дифференцирования связи для скоростей, не забывая, что координатные векторы подвижной системы координат также могут зависеть от времени.

Положение материального тела в условно неподвижной и инерциальной системе задаётся здесь вектором  , а в неинерциальной системе — вектором  . Положение начала координат второй системы отсчета в первой системе отсчета определяется вектором  . Угловая скорость вращения неинерциальной системы отсчета относительно инерциальной задаётся вектором  . Линейная относительная скорость тела по отношению к неинерциальной (вращающейся) системе отсчета ( считая ее при этом неподвижной ) задаётся вектором  .

Тогда ускорение   в инерциальной системе отсчета будет равно сумме:

.

24. Ускорение Кориолиса. Правило Жуковского.

Кинематическая теорема Кориолиса: абсолютное ускорение точки является векторной суммой трех ускорений - относительного, переносного и ускорения Кориолиса.

Ускорение Кориолиса равно удвоенному векторному произведению угловой скорости переносного движения на относительную скорость точки:  , следовательно по модулю ускорение Кориолиса:   (sin90=1).

Кориолисово ускорение обращаетсяв нуль, когда: 1) переносное движение - поступательное, т.е. омега переносное равно нулю; 2) в те моменты времени, когда в относительном движении точка останавливается, например. при изменении направления относительного движения.

Правило Жуковского: Кориолисово ускорение можно получить, спроецировав вектор радиальной скорости на плоскость, перпендикулярную вектору омега переносное, увеличив полученную проекцию радиальной скорости в 2*(омега переносное) раз и повернув ее на 90 градусов в направлении переносного вращения.