17. Определение ускорений точек плоской фигуры с помощью мцу.

(ответ взят из 16 вопроса, просто во всех формулах нужно выразить вместо расстояния до МЦС - ускорение точки)

18. Вращение твердого тела вокруг неподвижной точки. Углы Эйлера.

Движение твердого тела называется вращением вокруг неподвижной точки, если во все время движения одна и та же точка твердого тела остается неподвижной. Вращение твердого тела вокруг неподвижной точки называют сферическим движением, поскольку траектория любой точки тела располагается на поверхности сферы с центром в неподвижной точке тела.

Положение тела, как правило, определяется углами Эйлера: углом прецессии  , углом нутации  , углом собственного вращения  .

Линию OK пересечения координатных плоскостей Оху (на рис. изображена в виде заштрихованного овала) и OXY (ограничена белым овалом) назовем линией узлов. Тогда угол прецессии у определяет положение линии узлов ОК относительно неподвижной координатной оси Ох. Для изменения этого угла тело должно вращаться вокруг неподвижной оси Oz, называемой осью прецессии. Угол нутации   определяет положение подвижной оси OZ относительно неподвижной Oz и равен углу между этими осями. Изменение угла  сопровождается вращением тела вокруг линии узлов ОК, называемой осью нутации. Наконец, угол собственного вращения   характеризует вращение тела вокруг оси OZ, называемой осью собственного вращения. В подвижной плоскости OXY это угол между линией узлов ОК и подвижной осью ОХ.

Положительное направление отсчета углов Эйлера  ,   и  противоположно направлению движения часовой стрелки, если смотреть на поворот тела с положительных направлений осей Oz, ОК и OZ соответственно.

Уравнения вращения твердого тела вокруг неподвижно точки:  .

19. Скорости и ускорения точек тела при его вращении вокруг неподвижной точки.

20. Скорости и ускорения течек твердого тела при его свободном движении.

Переносное движение - поступательное движение вместе с полюсом. (Ve)

Относительное движение - вращательное движение относительно полюса. (Vr)

ρ = r0 + r

vM = dρ/dt = dr0/dt + dr/dt = v0 + ωr = (vM)e + (vM)r

a = dv/dt = dv0/dt + (dω/dt)*r + ω(dr/dt) = a0 + ε*r+ ω*r = a0 + a(вр) + а(ос) = (аМ)е + (аМ)r

(все что идет ниже, может не относиться к этому вопросу)

Докажем,

v = v0 + ω*r

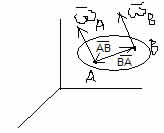
1) Полюс - т. А: vB = vA + ωS*AB

2) Полюс - т. В: vA = vB + ωB*BA = vB - ωB*AB

1) + 2) : (vB + vA) = (vA + vB) + ω*AB- ωB*AB

(ωA - ωB)*AB = 0

21. Сложное движение точки. Основные понятия.

Движение точки, исследуемое одновременно в основной и подвижной (подвижных) системах отсчета, называется сложным. В простейшем случае сложное движение точки состоит из относительного и переносного движений. Определим эти движения.

Рассмотрим сложное движение точки M, перемещающейся по отношению к подвижной системе O'XYZ, связанной с некоторым телом Qy которое в свою очередь совершает свободное движение по отношению к основной, условно неподвижной системе Oxyz.

Движение точки М по отношению к неподвижной системе отсчета Oxyz называется абсолютным, или сложным, состоящим из относительного движения по отношению к подвижной системе O'XYZ и переносного — движения подвижной системы отсчета O'XYZ по отношению к неподвижной системе Oxyz.

Положение точки М в подвижной системе координат O'XYZ характеризует радиус-вектор   с началом в точке О'. Траектория точки М в подвижной системе отсчета называется относительной траекторией и представляет собой годограф радиус-вектора  . Скорость движения точки М по отношению к осям подвижной системы координат называется относительной скоростью и обозначается Vr. Вектор Vr определяет скорость изменения с течением времени радиус-вектора   в подвижной системе O'XYZ и поэтому выражается его относительной, или локальной, производной по времени, 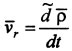 . Ускорение точки М в этом движении называется относительным ускорением и обозначается аr. Вектор аr характеризует скорость изменения вектора относительной скорости Vr в подвижной системе O'XYZ и поэтому выражается относительной, или локальной, производной по времени от Vr:  .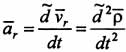

Движение подвижной системы O'XYZ по отношению к неподвижной Oxyz является для точки М переносным движением, а скорость и ускорение той неизменно связанной с подвижной системой отсчета точки А, с которой в данный момент времени совпадает точка М, называют переносными скоростью и ускорением точки М и обозначают Ve и ае.

Переносные скорость и ускорение точки М определяются по формулам:  , где вектора Vo' и ao' - скорость и ускорение точки О' подвижной системы координат.