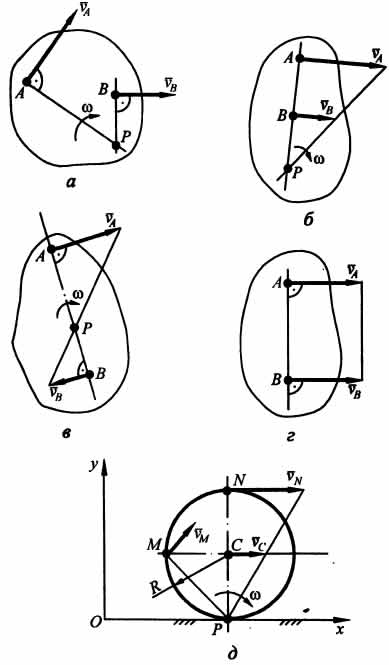
- •Траектория, скорость и ускорение точки при векторном способе задания движения.
- •Траектория, скорость и ускорение точки при задании движения в декартовой системе координат.
- •Скорость и ускорение точки при естественном способе задания движения.
- •Траектория, скорость и ускорение точки при задании движения на плоскости в полярных координатах.
- •Понятие о криволинейных координатах. Координатные линии и координатные оси.
- •Определение скорости точки при задании в криволинейных координатах . Пример.
- •Поступательное движение твердого тела. Траектории, скорости и ускорения точек тела.
- •Вращение твердого тела вокруг неподвижной оси. Скорости и ускорения точек тела (векторные и скалярные выражения).
- •Определение скоростей точек плоской фигуры с помощью мцс.
- •Соотношение между ускорениями двух точек плоской фигуры при плоском движении.
- •Способы определения углового ускорения при плоском движении.
- •Мгновенный центр ускорений. Способы нахождения.
- •Определение ускорений точек плоской фигуры с помощью мцу.
- •Вращение твердого тела вокруг неподвижной точки. Углы Эйлера.
- •Скорости и ускорения точек тела при его вращении вокруг неподвижной точки.
- •Скорости и ускорения течек твердого тела при его свободном движении.
- •Сложное движение точки. Основные понятия.
- •Полная и локальная производные вектора. Формула Бура.
- •Скорости и ускорения точки при сложном движении.
- •Ускорение Кориолиса. Правило Жуковского.
- •Сложение вращений твердого тела вокруг пересекающихся осей.
- •Сложение вращений твердого тела вокруг параллельных осей.
- •Пара вращений.
- •Аксиомы статики.
- •Основные виды связей и их реакции.
- •Система сходящихся сил. Условия равновесия.
- •Алгебраический и векторный моменты силы относительно точки.
- •Момент силы относительно оси.
- •Связь векторного момента силы относительно точки с моментом силы относительно
- •Аналитические выражения для моментов силы относительно осей координат.
- •Пара сил. Теорема о сумме моментов сил, составляющих пару, относительно
- •Векторный и алгебраический моменты пары сил.
- •Эквивалентность пар. Сложение пар. Условия равновесия пар сил.
- •Лемма о параллельном переносе силы.
- •Теорема о приведении произвольной системы сил к силе и паре сил – основная
- •Главный вектор и главный момент системы сил.
- •Условия равновесия произвольной системы сил. Частные случаи.
- •Трение качения. Коэффициент трения качения.
- •Центр системы параллельных сил. Формула для радиус-вектора и координат центра системы параллельных сил.
- •Центр тяжести тела. Методы нахождения центра тяжести.
- •1) Метод симметрии.
- •2) Метод разбиения.
- •3) Метод интегрирования.
Вращение твердого тела вокруг неподвижной оси. Скорости и ускорения точек тела (векторные и скалярные выражения).
Вращением твердого тела вокруг неподвижной оси (или просто вращательным движением) называется такое движение твердого тела, при котором в теле можно выделить прямую, все точки которой будут оставаться неподвижными во время движения. Эта прямая называется осью вращения твердого тела. Очевидно, что для ее задания достаточно указать как минимум две неподвижные точки в рассматриваемом теле, через которые она проходит.
Алгоритм задания вращательного движения может быть определен на основе следующего анализа. Введем неподвижную прямоугольную декартову систему координат Oxyz и аналогичную подвижную систему координат OXYZ, жестко связанную с рассматриваемым телом, расположив оси Oz и OZ на оси вращения тела (рис.).
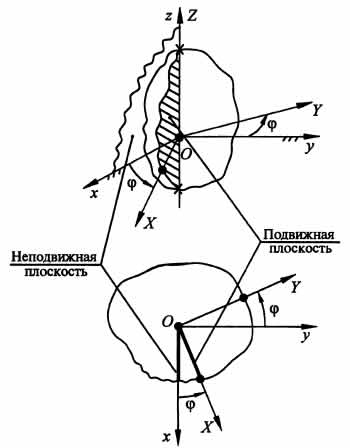
Пусть в начальный момент времени оси координат подвижной и неподвижной систем совпадали. Тогда положение вращающегося тела относительно неподвижной системы координат в любой текущий момент времени однозначно определится значением двугранного угла "фи" между неподвижной плоскостью Oxz и подвижной плоскостью OXZ, вращающейся вместе с рассматриваемым телом. Таким образом, при вращении вокруг неподвижной оси тело имеет одну степень свободы, так как его положение в неподвижной системе координат Oxyz однозначно определяется значением одного скалярного параметра — угла "фи". Уравнение, определяющее изменение этого угла как функции времени, общего вида: "фи" = "фи"(t), где "фи"(t) — непрерывная дважды дифференцируемая функция времени, называется законом вращения твердого тела вокруг неподвижной оси.
Угловую
скорость можно
определить и как вектор "омега",
расположенный на оси вращения и равный ![]() ,
где k — единичный вектор, задающий
положительное направление оси вращения,
или орт оси Oz (рис.).
,
где k — единичный вектор, задающий
положительное направление оси вращения,
или орт оси Oz (рис.).

Проекция
вектора угловой скорости на ось вращения
Oz: ![]() ,
т.е. она равна угловой скорости вращения
тела. Положительные направления
отсчета
,
т.е. она равна угловой скорости вращения
тела. Положительные направления
отсчета ![]() и
оси Oz соответствуют правой декартовой
системе координат.
и
оси Oz соответствуют правой декартовой
системе координат.
Численное
значение угловой скорости "омега"
равно модулю вектора "омега" и
определяется как модуль проекции
"омега"z либо как модуль угловой
скорости тела при его вращении вокруг
неподвижной оси: ![]() .
.
Единица измерения угловой скорости в СИ — радиан в секунду (рад/с).
Изменение
угловой скорости тела во времени
характеризуется его угловым
ускорением.
Угловым
ускорением тела называется первая
производная от угловой скорости или
вторая производная по времени от угла
поворота вокруг неподвижной оси: 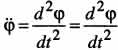 ,
где
,
где ![]() -
скаляоная алгебраическая величина.
-
скаляоная алгебраическая величина.
Как векторную
величину угловое
ускорение можно определить так: ![]() .
.
Проекция
углового ускорения на ось вращения
Oz: ![]() ,
т.е. она равна угловому ускорению тела.
Положительные направления отсчета
,
и
оси Oz соответствуют правой декартовой
системе координат.
,
т.е. она равна угловому ускорению тела.
Положительные направления отсчета
,
и
оси Oz соответствуют правой декартовой
системе координат.
Значение
(модуль) углового ускорения: ![]() .
.
Единица измерения углового ускорения в СИ - радиан на секунду в квадрате (рад/с2).
Теорема о проекциях скоростей двух точек твердого тела на прямую, проходящую через три точки.

Соотношение между скоростями двух точек плоской фигуры при плоском движении твердого тела.

Способы определения угловой скорости при плоском движении.


Мгновенный центр скоростей. Способы нахождения.
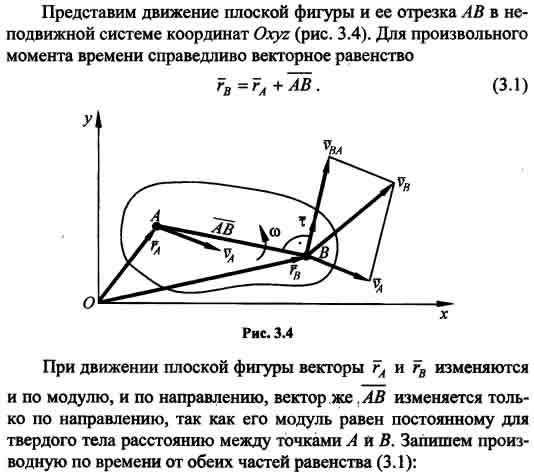
В любой момент времени при плоском движении фигуры существует единственная точка фигуры, скорость которой равна нулю. Эту точку называют мгновенным центром скоростей (МЦС). Найдем эту точку, обозначив ее Р.

Примем
точку Р за полюс фигуры. Тогда для ее
произвольной точки В можно записать:![]() ,
где PB — расстояние от МЦС — точки Р до
точки В; вектор vB перпендикулярен отрезку
РВ, направлен в сторону вращения фигуры
вокруг МЦС (см. рис. 3.5), а его модуль
пропорционален расстоянию от МЦС до
точки.
,
где PB — расстояние от МЦС — точки Р до
точки В; вектор vB перпендикулярен отрезку
РВ, направлен в сторону вращения фигуры
вокруг МЦС (см. рис. 3.5), а его модуль
пропорционален расстоянию от МЦС до
точки.
Таким образом, скорости точек плоской фигуры в данный момент времени вычисляются так же, как если бы фигура вращалась вокруг неподвижной оси, проходящей через МЦС перпендикулярно плоскости движения, с той же угловой скоростью "омега".