Определение скорости точки при задании в криволинейных координатах . Пример.
Скорость
точки М при
задании ее движения в криволинейных
координатах определится в виде векторной
суммы составляющих скоростей, параллельных
координатным осям: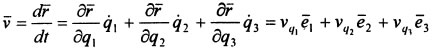 
.
Проекции скорости на соответствующие
координатные оси равны: 
.
Модуль скорости в ортогональной
криволинейной системе координат можно
рассчитать по зависимости: 
.
В приведенных формулах значения
производных и коэффициентов Ламе
вычисляют для текущего положения точки
М в пространстве.
Пример (может быть и не это): Скорость в сферической системе координат.
Координатами
точки в сферической системе координат
являются скалярные параметры r, "фи",
"тета", отсчитываемые так, как
показано на рис. Система уравнений
движения точки в данном случае имеет
вид: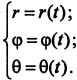 
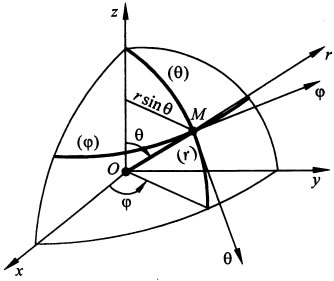
На
рис. изображены радиус-вектор r, проведенный
из начала координат, углы "фи" и
"тета", а также координатные линии
и оси рассматриваемой системы в
произвольной точке М траектории. Видно,
что координатные линии ("фи") и
("тета") лежат на поверхности сферы
радиусом r. Данная криволинейная система
координат также является ортогональной.
Ее оси Mr, М("фи") и М("тета") и
соответствующие им единичные векторы
er, e("фи"), е("тета"), определяютщие
положительные напревления осей, взаимно
перпендикулярны. Декартовы координаты
могут быть выражены через криволинейные
координаты так: 
.
Тогда коэффициент Ламе: 
;
проекции скорости точки на оси сферической
системы координат 
,
а модуль 
.
Поступательное движение твердого тела. Траектории, скорости и ускорения точек тела.
Поступательным движением твердого тела называется такое его движение, при котором прямая, проходящая через любые две точки в этом теле, будет оставаться параллельной своему первоначальному положению во все время движения. Заметим, что при этом траектории точек тела могут быть любыми и иметь форму прямой, окружности, пространственной кривой и т.д.
Примерами поступательного движения служат движения контактной рейки трамвайного пантографа относительно вагона, кабины колеса обозрения в парке относительно земли, ступеней эскалатора относительно пола в метро и т. д.
Свойства поступательного движения: 1) траектории всех точек тела, совершающего поступательное движение, конгруэнтны, т. е. одинаковы, и могут быть получены одна из другой параллельным переносом; 2) скорости всех точек тела одинаковы; 3) ускорения всех точек тела одинаковы.
Эти
выводы можно подтвердить на основании
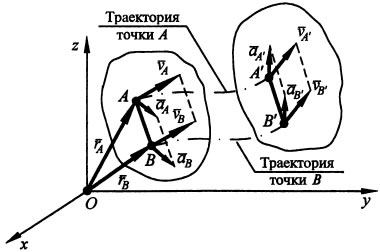
следующего анализа. Дня двух любых точек
А и В тела, совершающего поступательное
движение (рис.), можно записать
соотношение 
,
где АВ=const - вектор, имеющий постоянные
модуль и направление во время движения,
так что траектории точек А и В как
годографы соответствующих радиус-векторов
rA и rB оказываются смещенными в любой
момент времени одна относительно другой
на одну и ту же величину в одном и том
же направлении, что и доказывает первое
свойство.
Дифференцируя левую и правую части приведенного выше векторного соотношения и учитывая, что dAB/dt=0, получаем drB/dt =drA/dt, или VB = VA. Дифференцируя по времени левую и правую части полученного соотношения для скоростей, находим dVB/dt=dVA/dt, или аB = аА. На основании вышеизложенного можно сделать следующий вывод: чтобы задать движение и определить кинематические характеристики тела, совершающего поступательное движение, достаточно задать движение одной его любой точки (по- люса) и найти ее кинематические характеристики.
Как и материальная точка, тело при его поступательном движении будет иметь одну степень свободы при движении по направляющей, задающей траекторию его точкам; две степени свободы в случае движения на плоскости (при постоянном контакте с ней хотя бы одной точкой) и три степени свободы в общем случае движения в пространстве.