4. Траектория, скорость и ускорение точки при задании движения на плоскости в полярных координа­тах.

Если движение точки происходит в некоторой плоскости, то иногда целесообразно использовать полярную систему координат. Положение точки М в ней определяется координатами r и "фи", являющимися скалярными величинами.

Расположение полярной оси (луча, проведенного на плоскости из некоторой точки О) выбирают в плоскости движения точки, исходя из удобства решения задачи.

Полярный радиус r - скалярный неотрицательный параметр, равный длине отрезка ОМ, т.е. расстоянию от начала координат (точки О) до точки М.

Полярный угол "фи" - это угол между полярной осью и илнией ОМ (за положительное значение значение угла принимают направление, противоположное направлению движения часовой стрелки).

Для задания движения точки в полярной системе коодинат необходимо иметь уравнение движения в виде:  Данная система является также параметрической формой записи уравнения траектории точки. Если из системы исключить время, то уравнение траектории можно получить в форме:  .

В полярной системе координат радиус-вектор точки, проведенный из центра О, равен   и выражается так:  .

Вектор скорости представляется в виде суммы двух векторов, каждый из которых является составляющей скорости по направлению, задаваемому векторами r0 и p0 соответственно. Первое слагаемое называется радиальной составляющей, а второе - трансверсальной составляющей скорости точки:  . Проекции скорости на радиальную и трансверсальную оси имею вид  . Так как составляющие скорости взаимно перпендикулярны, то ее модуль:  .

Ускорение точки:  , где   - радиальная и трансверсальная составляющие ускорения точки соответственно. Так как составляющие ускорения взаимно перпендикулярны, то его модуль:  .

5. Понятие о криволинейных координатах. Координатные линии и координатные оси.

Движение точки в пространстве можно считать заданным, если известны законы изменнеия трех ее декартовых координат x, y, z как функции времени. Однако в некоторых случаях пространственного движения материальных точек (например, в областях, ограниченных поверхностями различной формы) использование уравнений движения в декартовых координатах неудобно, так как они становятся слишком громоздкими. В таких случаях можно выбрать другие три независимых скалярных параметра q1, q2, q3, называемых криволинейными, илиобобщенными координатами, которые также однозначно определяют положение точки в пространстве.

Тогда радиус-вектор точки может быть выражен функцией как декартовых, так и криволинейных координат:  . При этом следует иметь в виду, что декартовы координаты точки могут также быть выражены в виде функций, зависящих от криволинейных координат:  . Для задания движения точки в криволинейных координатах необходимо иметь уравнения движения точки в виде:  .

Характеристиками криволинейной системы координат являются координатные линии и координатные оси.

Координатные линии (qi), проходящие через любую выделенную точку М пространства с фиксированными значениями координат q1M, q2M, q3M и соответствующие каждой i-ой криволинейной координате, можно определить как годограф радиус-вектора riM точки М, изменяющегося в результате варьирования одной выделенной i-ой криволинейной координаты при условии, что другие сохраняются постоянными и равными их значениям в выделенной точке:

Касательная к i-ой координатной линии в данной точке называется координатной осью Mqi, относящейся к i-ой криволинейной координате в данной точке. Положительные направления координатных осей задаются единичными векторами, которые называются базисами. Они определяются через частные производные от радиус-вектора точки по i-ой обобщенной координате в данной точке M: 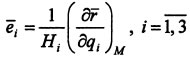 . Здесь   - параметр, который называется i-ым коэффициентом Ламе и равен значению модуля частной производной от радиус-вектора точки по i-ой криволинейной координате, вычисленной в данной точке М. Каждый из векторов ei имеет направление, соответствующее направлению движения точки конца радиус-вектора riM при возрастанийй i-ой обобщенной координаты.