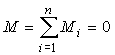35. Пара сил. Теорема о сумме моментов сил, составляющих пару, относительно

произвольной точки.

Пара сил - система двух сил равных по модулю и противоположных по направлению.

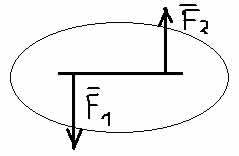
F1 = -F2

R* = F1 - F2 = 0

AC/F2 = BC/(R*) (стремится к бесконечности)

(F1,F2) не эквивалентны 0

Момент пары сил - произведение одной из сил на ее плечо.

M(F1,F2) = M12 = ±F1*d = ±F2*d

Векторный момент пары сил.

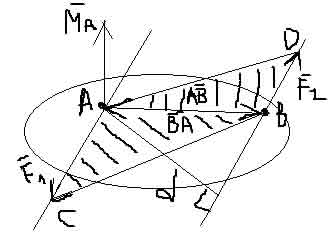
MA = AB * F2

MA = F2 * AB * sinα = F2d

MB = BA * F1 = F1 * d

M = MA = MB = S(ACBD)

Теорема о сумме моментов сил, составляющих пару, относительно произвольной точки: Сумма моментов сил, входящих в состав пары сил относительно любой точки не зависит от ее выбора и равна моменту этой пары сил.

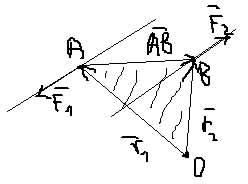
F1 = -F2

Mo(F2) + Mo(F1) = r2*F2 + r1*F1 = r2*F2 - r1*F2 = (r2 - r1)*F2 = AB * F2 = M(F1,F2)

36. Векторный и алгебраический моменты пары сил.

Алгебраический момент M=±F•d (пара). M=±dF1=±dF2=±2SΔABC= ±S. Он не меняется при перемещении сил вдоль линии их действия (ни плечо, ни направление вращения не меняются).

Векторный момент – вектор M=M(F,F’), направлен перпендикулярно плоскости пары в ту сторону, откуда видно стремление пары повернуть тело против часовой хода стрелки, его модуль равен алгебраическому моменту пары. M(F1,F2)=BAxF1=ABxF2.

37. Эквивалентность пар. Сложение пар. Условия равновесия пар сил.

Эквивалентность пар сил. Две пары сил с равными моментами эквивалентны. Или (F,F') ~ (P,P') , если M(F,F') ~ M(P,P'). Эквивалентность пар сил сразу следует из свойств пары сил. Очевидно, что только при равных моментах пар сил их действие на твердое тело будет одинаковым.

Сложение пар сил. Система пар сил эквивалентна одной паре, момент которой равен сумме моментов пар, образующих систему:

(8)

где M₁ = M(F₁,F₁'), M₂ = M(F₂,F₂'), ..., M_n = M(F_n,F_n').

Необходимым и достаточным условием равновесия системы пар, лежащих в одной плоскости, является равенство нулю алгебраической суммы моментов всех пар системы:

38. Лемма о параллельном переносе силы.

Сила, приложенная к какой-либо точке твердого тела, эквивалентна такой же силе, приложенной к любой другой точке тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения. Доказательство: пусть дана сила F. Приложим к какой-либо точке В систему F’ и F”. |F|=|F’|=|F”|. F~(F,F’,F”), т.к. (F’,F”) ~ 0, то  F ~ (F,F’,F”) ~ (F,F’,F”) ~ (F’,M(F,F”)). Но M(F,F”)=BAxF=MB(F). Получаем: F ~ (F’,M(F,F”)) Ч. т. д.

39. Теорема о приведении произвольной системы сил к силе и паре сил – основная

теорема статики.

40. Главный вектор и главный момент системы сил.

41. Условия равновесия произвольной системы сил. Частные случаи.

Условия равновесия можно сформулировать так: для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций всех сил на оси декартовой системы координат равнялись нулю и суммы моментов всех сил относительно этих осей также равнялись нулю.

Частные случаи.

Условия равновесия пространственной системы параллельных сил.

Если силы, действующие на твердое тело, параллельны между собой, то можно выбрать такую систему координат, когда одна из ее осей, например Oz, параллельна направлению действия сил (рис.). Тогда из шести аналитических условий равновесия три выполняются тождественно, и система параллельных сил будет иметь только три условия равновесия:

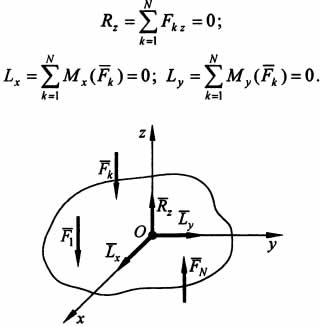
Условия равновесия плоской системы сил.

Для плоской системы сил условия равновесия будут частным случаем уравнений 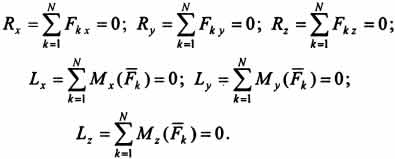 , определяющих условия равновесия пространственной системы сил. Например, если силы расположены в плоскости Оху, то аналитические условия равновесия можно записать в виде: 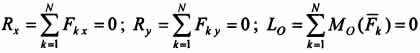 Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма алгебраических моментов этих сил относительно любого центра О были равны нулю. Алгебраическим моментом силы относительно точки называют момент силы относительно оси, проходящей через данную точку перпендикулярно плоскости, в которой расположена сила и точка. Вместо  иногда удобно применить условия равновесия в виде уравнений трех моментов: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы алгебраических моментов всех этих сил относительно любых трех центров А, В, С, не лежащих на одной прямой, были равны нулю:  .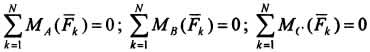

Необходимость утверждения следует из того, что третье условие   справедливо для любой точки. Достаточность докажем методом от противного, используя теорему о приведении произвольной системы сил к центру. Допустим, что плоская система сил не находится в равновесии. Тогда, приводя ее поочередно к точкам А, В, С, будем иметь в этих точках равнодействующую R . Для выполнения равенств   равнодействующая должна пройти одновременно через все три точки, а это невозможно, так как точки не лежат на одной прямой. Следовательно, равнодействующая равна нулю и система сил, удовлетворяющая равенствам  , находится в равновесии.

42. Теорема Вариньона о моменте равнодействующей силы.

Если все силы приложены в одной точке, то  .

Выражение представляет собой векторную запись теоремы Вариньона.

Теорема Вариньона: момент равнодействующей относительно какой-либо точки равен сумме моментов составляющих сил относительно той же точки.

43. Зависимость между главными моментами системы сил относительно двух центров приведения.

44. Инварианты системы сил. Частные случаи приведения.

45. Трение скольжения. Законы Кулона. Угол и конус трения.

Между движущимися телами в плоскости их соприкосновения возникает сила трения скольжения. Обусловлено это прежде всего шероховатостью соприкасающихся поверхностей и наличием сцепления у прижатых тел.

В инженерных расчетах обычно пользуются установленными опытным путем закономерностями, которые с некоторой степенью точности отражают действие силы трения. Эти закономерности называют законами трения скольжения (Кулона). Их можно сформулировать следующим образом.

1. При стремлении сдвинуть одно тело относительно другого в плоскости их соприкосновения возникает сила трения F , модуль которой может принимать любые значения от нуля до Fmax, т. е.  . Сила трения приложена к телу и направлена в сторону, противоположную возможному направлению скорости точки приложения силы.

2. Максимальная сила трения равна произведению коэффициента трения f на силу нормального давления N:  .

Коэффициент трения f — безразмерная величина, зависящая от материалов и состояния поверхностей соприкасающихся тел (шероховатость, температура, влажность и т. п.). Определяют его опытным путем.

Различают коэффициенты трения покоя и трения скольжения, причем последний, как правило, зависит и от скорости скольжения. Коэффициент трения покоя соответствует такой максимальной силе трения Fmax, при которой имеется предельное состояние равновесия. Малейшее увеличение внешних сил может вызвать движение. Коэффициент трения покоя, как правило, немного больше коэффициента трения скольжения. С увеличением скорости скольжения значение коэффициента трения скольжения сначала незначительно уменьшается, а затем остается практически неизменным. Значения коэффициентов трения для некоторых пар трения следующие: дерево по дереву 0,4-0,7; металл по металлу 0,15-0,25; сталь по льду 0,027.

3. Максимальная сила трения в довольно широких пределах не зависит от площади соприкасающихся поверхностей.

Силу трения скольжения иногда называют силой сухого трения.

Реакция шероховатой поверхности. Угол трения.

Реакция идеально гладкой поверхности, как уже говорилось выше, направлена по нормали к поверхности. На шероховатой поверхности могут возникать силы трения скольжения. Поэтому реакцию шероховатой поверхности представим в виде двух составляющих: нормальной реакции N (равна по модулю силе нормального давления) и перпендикулярной ей силы трения F.

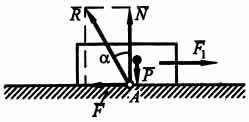
Полная реакция R=N + F всегда отклонена от нормали к поверхности на некоторый угол "альфа". На рисунке видно, что  . Если тело лежит на горизонтальной шероховатой поверхности и на него не действуют никакие внешние силы, кроме силы тяжести, то F = 0, а полная реакция R = N и перпендикулярна опорной поверхности. Приложив к телу силу F1, мы стремимся вызвать его движение, но оно не происходит, так как возникает сила трения F = -F1, причем  . С увеличением силы F1 будет возрастать и сила F . Наконец, при F1 = Fmax наступит предельное состояние равновесия, при котором полная реакция R отклонится от вертикали на угол "альфа"max, называемый углом трения. Обозначив его через "фи", получим  .

Тангенс угла трения равняется коэффициенту трения. Полная реакция неидеальной связи при равновесии имеет направление в пределах угла трения.

Конус трения.

Рассмотрим равновесие невесомого тела на горизонтальной шероховатой плоскости под действием наклонной силы F1, стремящейся его сдвинуть.

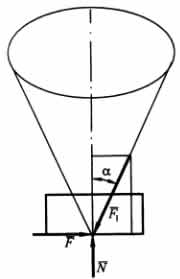
Тело будет сдвинуто только тогда, когда  > Fmax =  . Предельному случаю равновесия соответствует такой угол наклона a, при котором выполняется равенство  =  , или tgα = f. Если tgα<=f, то как бы не возрастала сила F1, тело сдвинуть с места невозможно. Возрастающей сдвигающей силе   будет противостоять пропорционально ей увеличивающаяся сила трения  .

Поворачивая вокруг вертикали вектор силы F1 и сохраняя при этом предельное равновесие, опишем конус, называемый конусом трения. Если свойства соприкасающихся поверхностей во всех направлениях одинаковы, то угол а будет постоянным, а конус трения круговым. Конус трения обладает тем замечательным свойством, что если действующая на тело сила находится внутри него, то тело всегда будет находиться в равновесии. Этим объясняются известные явления заклинивания, или самоторможения тел.