30. Система сходящихся сил. Условия равновесия.

Систему сил, приложенных к твердому телу, называют системой сходящихся сил, если линии действия всех сил пересекаются в одной точке.

Система сходящихся сил эквивалентна одной равнодействующей силе, которую можно определить замыкающим вектором R* силового многоугольника, построенного на векторах-сипах системы сходящихся сил. Другими словами, равнодействующая системы сходящихся сил равна их геометрической сумме.

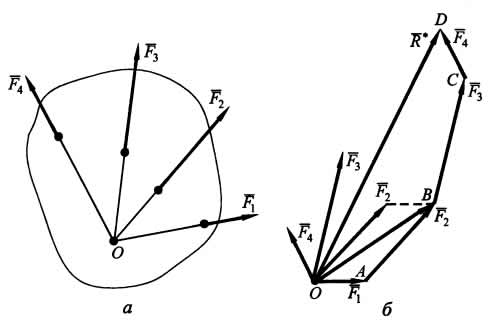
Многоугольник OABCD называется силовым многоугольником.

Условия равновесия системы сходящихся сил.

Так как система сходящихся сил эквивалентна одной равнодействующей, то тело под действием такой системы сил будет находиться в равновесии тогда, когда равнодействующая равна нулю, т. е. силовой многоугольник должен быть замкнут. Условия равновесия в векторной и аналитической форме имеют соответственно следующий вид: 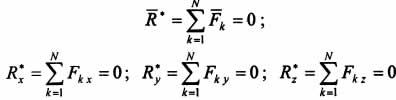 . Данные равенства содержат заданные и неизвестные величины. Их называют уравнения равновесия.

31. Алгебраический и векторный моменты силы относительно точки.

 Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы относительно этой точки взятое со знаком плюс или минус.

Векторным моментом силы относительно точки называют вектор, приложенный в этой точке и равный по модулю произведению силы на плечо силы относительно этой точки. Векторный момент силы направлен перпендикулярно плоскости, в которой лежат сила и моментная точка, таким образом, что с его конца можно видеть стремление силы вращать тело против движения часовой стрелки.

32. Момент силы относительно оси.

Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения плоскостью. Момент силы относительно оси считается положительным, если проекция силы на плоскость, перпендикулярную к оси, стремится вращать тело вокруг положительного направления оси против движения часовой стрелки, и отрицательным, если она стремится вращать тело по движению часовой стрелки:

 M_z(F) = M_o(F_П) = ±hF_П,

где F_П  – вектор проекции силы F  на плоскость  П, перпендикулярную к оси  Oz, точка O  – точка пересечения оси Oz  с плоскостью  П.

33. Связь векторного момента силы относительно точки с моментом силы относительно

оси, проходящей через эту точку.

Момент силы относительно точки О - это вектор, модуль которого равен произведению модуля силы на плечо. Если известен радиус-вектор r⃗  точки приложения силы F⃗  относительно точки О, то момент этой силы относительно О выражается следующим образом:

M⃗ O(F⃗ )=r⃗ ×F⃗ .

34. Аналитические выражения для моментов силы относительно осей координат.

Момент силы относительно оси - проекция на эту ось момента силы относительно любой точки лежащей на оси.

Момент сил относительно декартовых осей координат (проекции момента силы на эти оси).

                          | i     j     k |

M0(F) = r * F = | x    y    z | = (y*Fz - z*Fy)*i + (z*Fx - x*Fz)*j + (x*Fy - y*Fx)*k =

                          | Fx Fy Fz | = Mox(F)*i + Moy(F)*j + Moz(F)*k

Mox(F)=y*Fz - z*Fy

Moy(F)=z*Fx - x*Fz

Moz(F)=x*Fy - y*Fx