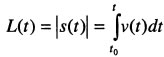1. Траектория, скорость и ускорение точки при векторном способе задания движения.

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета. 

Кривая, которая вычерчивается концом какого-либо вектора, назыв. годографом этого вектора. Т.е. траектория – годограф радиус-вектора.

Пусть движение точки относительно тела отсчета задано ее радиус-вектором r(t). Тогда, по определению, скоростью точки будет векторная производная радиус-вектора r по скалярному аргументу - времени t:

По определению ускорение является производной по времени от вектора скорости:

2. Траектория, скорость и ускорение точки при задании движения в декартовой системе координат.

Положение точки М в пространстве с использованием данной системы координат задается ее координатами x, y, z. Чтобы знать положение точки в пространстве в любой момент времени необходимо иметь уравнения движения точки в виде: x=x(t), y=y(t), z=z(t).

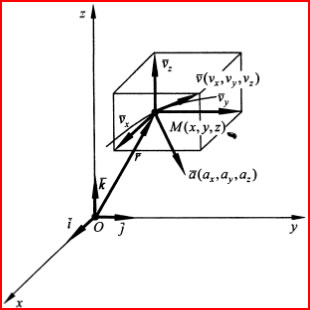
x=x(t), y=y(t), z=z(t) - представляют собой уравнения движения точки в декартовой системе координат и одновременно являются уравнениями траектории точки, записанными в параметрической форме, где параметром является время t. Чтобы найти уравнение траектории в форме непосредственной зависимости между координатами x, y, z, из системы уравнений x=x(t), y=y(t), z=z(t) необходимо исключить время. В таком случае траекторию будет определять, например, система уравнений вида: f1(x,y)=0, f2(x,z)=0. Следовательно, траектория представляет собой линию пересечения цилиндрических поверхностей, уравнения которых составляют систему f1(x,y)=0, f2(x,z)=0.

Скорость:    . Таким образом, скорость точки представляет собой сумму составляющих векторов, параллельных осям декартовой системы координат:  , где  , а ее численное значение (модуль) определяется по формуле:  .

Ускорение:  , проекции ускорения на оси декартовой системы координат будут  , составляющие ускорения, параллельные осям координат, определятся как  , а численное значение ускорения будет равно:  . Проекцию ускорения на ось, совпадающую по направлению с вектором скорости. для определения характера движения точки (т.е. ускоренно или замедленно она движется) можно в данном случае найти, в виде:  .

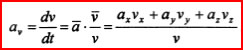3. Скорость и ускорение точки при естественном способе задания движения.

Если траектория точки известна (т.е. в некоторой системе отсчета определена графически, с помощью уравнения или другим образом), то задать движение точки можно естественным способом. Для этого необходимо: зафиксировать на трактории точку начала отсчета, выбрать положительное и отрицательное направления отсчета дуговой координаты и указать уравнение движения точки по траектории в виде S=S(t).

Скалярный параметр S в данном случае имеет смысл криволинейной (дуговой) координаты, модуль которой определяет текущее расстояние по траектории от начала отсчета (точки О) до подвижной точки М, а знак показывает, по какую сторону от начала отч=счета находится точка М на траектории.

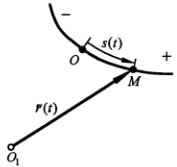
Следует отметить, что уравнение движения в форме S=S(t) определяет текущее положение точки именно на траектории, при этом может быть установлена взаимно однозначная связь между значениями координаты S и радиус-вектором точки М в той системе отсчета, в которой определена в рассматриваемом случае траектория движения точки. Тогда радиус-вектор точки может быть представлен в виде функциональной зависимости от параметра S в виде r=r(S).

Модуль скорости, т.е. ее численное значение, при естественном способе задания движения точки определятся так:  .

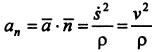Ускорение составляет сумму касательной и нормальной составляющих:  , где   и  . Следовательно:  .

Дополнение: Значение пути -