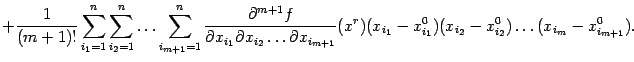- •1. Первообразная и неопределенный интеграл. Теорема об общем виде
- •2. Основные свойства неопределенных интегралов.
- •3. Метод интегрирования разложением и подстановкой. Теорема о замене
- •4. Метод интегрирования по частям. Теорема.
- •5. Интегрирование простейших дробей.
- •6. Интегрирование дробно-рациональных функций.
- •7. Интегрирование иррациональных выражений.
- •8. Интегрирование тригонометрических функций.
- •17.Несобственные интегралы с бесконечными пределами. Теорема о сходимости таких интегралов.
- •18. Несобственные интегралы от неограниченных функций.
- •19. Абсолютная сходимость несобственных интегралов.
- •20. Числовые ряды. Частичные суммы. Сходимость ряда. Теорема об общем члене сходящегося ряда.
- •21. Основные свойства рядов. Остаток ряда. Теорема об остатке ряда.
- •22. Положительные ряды. Признаки сходимости (теоремы сравнения)
- •23. Признак Даламбера.
- •24. Радикальный признак Коши.
- •25. Интегральный признак Коши-Маклорена.
- •26. Знакопеременные ряды. Понятие абсолютной сходимости. Теорема Коши об абсолютной сходимости.
- •27. Условная сходимость рядов. Теорема Лейбница.
- •28. Функциональные ряды. Область сходимости.
- •29. Степенные ряды. Теорема Абеля.
- •30. Ряды Тейлора. Критерий разложимости функции в ряд Тейлора.
- •35. Линейные уравнения первого порядка. Метод вариации произвольной постоянной (Лагранжа).
- •36. Уравнение Бернулли.
- •37. Задача Коши для уравнения первого порядка, разрешенного относительно производной.
- •38. Дифференциальные уравнения порядка выше первого. Два типа уравнений, метод решений которых понижение порядка.
- •39. Линейная зависимость функций. Определитель Вронского.
- •40. Однородные линейные дифференциальные уравнения с постоянными коэффициентами.
- •41. Неоднородные линейные дифференциальные уравнения с постоянными коэффициентами.
- •46. Частные производные высших порядков. Дифференцируемость функций нескольких переменных.
- •47. Дифференцирование сложных функций многих переменных.
- •48. Инвариантность формулы первого дифференциала.
- •49. Касательная плоскость и нормаль к поверхности.
- •50. Полные дифференциалы высших порядков.
- •51. Формула Тейлора для функции нескольких переменных.
- •52. Экстремум функции двух переменных. Необходимое условие экстремума. Достаточное условие экстремума.
46. Частные производные высших порядков. Дифференцируемость функций нескольких переменных.
Это частные производные, чей порядок выше единицы.
Теорема:
Если функция z
= f
(x;
y)
дифференцируема в точке M
(x;
y),
то она непрерывна в этой точке и имеет
в ней частные производные
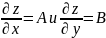
Теорема:
Если функция z
= f
(x;
y)
имеет непрерывные частные производные
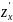 и
и
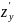 в точке M(x;y),
то она дифференцируема в этой точке и
ее полный дифференциал равен dz=
в точке M(x;y),
то она дифференцируема в этой точке и
ее полный дифференциал равен dz=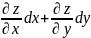
47. Дифференцирование сложных функций многих переменных.
Пусть z = f(x; y) – функция двух переменных x и y, каждая из которых является функцией независимой переменной t: x=x(t), y=y(t). В этом случае функция z=f(x(t); y(t)) является сложной функцией одной независимой переменной t, переменные x, t – промежуточные переменные.
Теорема: Если z = f(x; y) – дифференцируемая в точке M(x; y) ∈ D функция и x=x(t) и y=y(t) – дифференцируемые функции независимой переменной t, то производная сложной функции z=f(x(t); y(t)) вычисляется по формуле
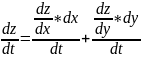
48. Инвариантность формулы первого дифференциала.
Используя правило дифференцирования сложной функции, можно показать, что полный дифференциал обладает свойством инвариантности: полный дифференциал функции z = f(x; y) сохраняет один и тот же вид независимо от того, являются ли аргументы независимыми переменными или функциями независимых переменных.
Пусть
z
= f(x;
y),
где x,
y
– независимые переменные. Тогда полный
дифференциал (1 порядка) функции имеет
вид
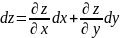 .
.
49. Касательная плоскость и нормаль к поверхности.
Пусть
имеется поверхность, заданная уравнением F
(x,
y,
z)
= 0.
Плоскость, в которой расположены все
касательные прямые к линиям на поверхности,
проходящим через данную точку 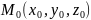 ,
называется касательной
плоскостью к
поверхности в точке
.
Если
поверхность задана уравнением F
(x,
y,
z)
= 0,
то уравнение касательной плоскости к
этой поверхности в точке
, записывается
в виде:
,
называется касательной
плоскостью к
поверхности в точке
.
Если
поверхность задана уравнением F
(x,
y,
z)
= 0,
то уравнение касательной плоскости к
этой поверхности в точке
, записывается
в виде:
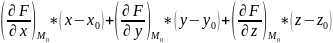 =0
=0
Прямая, проведенная через точку , поверхности F (x, y, z) = 0, перпендикулярно к касательной плоскости называется нормалью к поверхности.
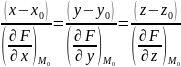
50. Полные дифференциалы высших порядков.
Если
функция z
= f(x;
y)
имеет непрерывные частные производные
второго порядка, то дифференциал второго
порядка определяется так: 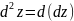
Символически
общий вид дифференциала n-го
порядка от функции z
= f(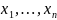 ) выглядит
следующим образом:
) выглядит
следующим образом:
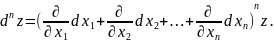
где z
= f(
),
а 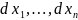 произвольные
приращения независимых переменных
.
Приращения
рассматриваются
как постоянные и остаются одними и теми
же при переходе от одного дифференциала
к следующему. Сложность выражения
дифференциала возрастает с увеличением
числа переменных.
произвольные
приращения независимых переменных
.
Приращения
рассматриваются
как постоянные и остаются одними и теми
же при переходе от одного дифференциала
к следующему. Сложность выражения
дифференциала возрастает с увеличением
числа переменных.
51. Формула Тейлора для функции нескольких переменных.
Теорема:
Пусть функция f(x) задана
в области D и
имеет в ней все
частные производные до порядка m+1 включительно.
Пусть
и
имеет в ней все
частные производные до порядка m+1 включительно.
Пусть ![]() и
и ![]() -
две точки области D
такие, что весь отрезок между ними
целиком лежит в D .
Тогда для некоторой точки
-
две точки области D
такие, что весь отрезок между ними
целиком лежит в D .
Тогда для некоторой точки 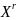 этого
отрезка имеет место равенство
этого
отрезка имеет место равенство
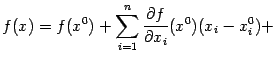
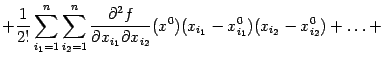
|
|
|
|
|
|
|
|