
- •1. Первообразная и неопределенный интеграл. Теорема об общем виде
- •2. Основные свойства неопределенных интегралов.
- •3. Метод интегрирования разложением и подстановкой. Теорема о замене
- •4. Метод интегрирования по частям. Теорема.
- •5. Интегрирование простейших дробей.
- •6. Интегрирование дробно-рациональных функций.
- •7. Интегрирование иррациональных выражений.
- •8. Интегрирование тригонометрических функций.
- •17.Несобственные интегралы с бесконечными пределами. Теорема о сходимости таких интегралов.
- •18. Несобственные интегралы от неограниченных функций.
- •19. Абсолютная сходимость несобственных интегралов.
- •20. Числовые ряды. Частичные суммы. Сходимость ряда. Теорема об общем члене сходящегося ряда.
- •21. Основные свойства рядов. Остаток ряда. Теорема об остатке ряда.
- •22. Положительные ряды. Признаки сходимости (теоремы сравнения)
- •23. Признак Даламбера.
- •24. Радикальный признак Коши.
- •25. Интегральный признак Коши-Маклорена.
- •26. Знакопеременные ряды. Понятие абсолютной сходимости. Теорема Коши об абсолютной сходимости.
- •27. Условная сходимость рядов. Теорема Лейбница.
- •28. Функциональные ряды. Область сходимости.
- •29. Степенные ряды. Теорема Абеля.
- •30. Ряды Тейлора. Критерий разложимости функции в ряд Тейлора.
- •35. Линейные уравнения первого порядка. Метод вариации произвольной постоянной (Лагранжа).
- •36. Уравнение Бернулли.
- •37. Задача Коши для уравнения первого порядка, разрешенного относительно производной.
- •38. Дифференциальные уравнения порядка выше первого. Два типа уравнений, метод решений которых понижение порядка.
- •39. Линейная зависимость функций. Определитель Вронского.
- •40. Однородные линейные дифференциальные уравнения с постоянными коэффициентами.
- •41. Неоднородные линейные дифференциальные уравнения с постоянными коэффициентами.
- •46. Частные производные высших порядков. Дифференцируемость функций нескольких переменных.
- •47. Дифференцирование сложных функций многих переменных.
- •48. Инвариантность формулы первого дифференциала.
- •49. Касательная плоскость и нормаль к поверхности.
- •50. Полные дифференциалы высших порядков.
- •51. Формула Тейлора для функции нескольких переменных.
- •52. Экстремум функции двух переменных. Необходимое условие экстремума. Достаточное условие экстремума.
35. Линейные уравнения первого порядка. Метод вариации произвольной постоянной (Лагранжа).
Линейное уравнение первое порядка называется линейным, если его можно записать в виде y’+p(x)*y=g(x), где p(x) и g(x) – заданные функции, в частности – постоянные.
Метод
вариации: Рассмотрим
уравнение без правой части. В этом
уравнении переменные делятся:
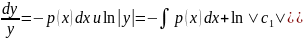 .
Таким образом,
.
Таким образом,
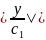 =
=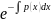 ,
т.е. y=±
,
т.е. y=±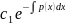 или y=c
или y=c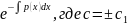 .
.
Метод
вариаций произвольной постоянной
состоит в том, что постоянную с в
полученном решении заменяем функцией
с(х), т.е. полагаем с=с(х). Решение ищем в
виде y=c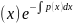 .
.
36. Уравнение Бернулли.
Это
уравнение вида
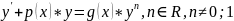 (1).
Его можно привести к линейному. Если
n=0,
то ДУ – линейное, а при n=1
– с разделяющимися переменными. В общем
случае, разделив уравнениена
(1).
Его можно привести к линейному. Если
n=0,
то ДУ – линейное, а при n=1
– с разделяющимися переменными. В общем
случае, разделив уравнениена
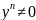 ,
получим:
,
получим:
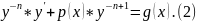 Выполнив замену
Выполнив замену
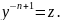 Тогда
Тогда
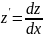 =(1-n)*
=(1-n)*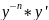 .
Отсюда находим
.
Отсюда находим
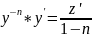 .
Уравнение (2) принимает вид
.
Уравнение (2) принимает вид
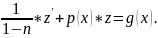
Последнее
уравнение является линейным относительно
z.
Решение его известно. Таким образом,
подстановка z=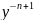 сводит уравнение (1) к линейному.
сводит уравнение (1) к линейному.
37. Задача Коши для уравнения первого порядка, разрешенного относительно производной.
Если
в уравнении y’’=f(x;
y;
y’)
функция f(x;
y;
y’)
и ее частные производные
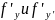 непрерывны в некоторой области D
изменения переменных x,
y,
y’,
то для всякой точки (
непрерывны в некоторой области D
изменения переменных x,
y,
y’,
то для всякой точки (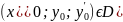 существует
единственное решение y=
существует
единственное решение y=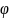 (x)
уравнения, удовлетворяющее заданным
начальным условиям.
(x)
уравнения, удовлетворяющее заданным
начальным условиям.
38. Дифференциальные уравнения порядка выше первого. Два типа уравнений, метод решений которых понижение порядка.
ДУ второго порядка в общем случае записывается в виде F(x;y;y’;y’’)=0 или в виде y’’=f(x; y; y’). Решением ДУ называется всякая функция y= (x), которая при подстановке в уравнение обращает его в тождество.
1 тип: y’’=f(x). Решается непосредственным интегрированием или вводя новую функцию, используя замену.
2 тип: y’’=f(x;y’) (не содержит явно искомой функции y)
Решается с помощью замены и вводя новую функцию.
3 тип: y’’=f(y;y’) (не содержит явно независимой переменной х)
Решается с помощью замены и вводя новую функцию.
39. Линейная зависимость функций. Определитель Вронского.
Определитель Вронского применяется для решения дифференциальных уравнений, например для того, чтобы узнать, являются ли найденные решения однородного линейного дифференциального уравнения (либо системы уравнений) линейно независимыми. Это помогает в поиске его общего решения.
Теорема: Если функции y1(x),…ym(x) линейно зависимы на (a; b) и имеют производные до (m-1)-го порядка, то определитель

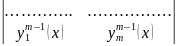 =0
(
=0
(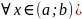
40. Однородные линейные дифференциальные уравнения с постоянными коэффициентами.
Пусть
дано ЛОДУ в виде y’’+p*y’+q*y=0,
p
и q
– постоянны. Частные решения выглядят
так: y=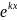 .
Дифференцируя и подставляя выражения
получаем
.
Дифференцируя и подставляя выражения
получаем
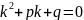 ,
,
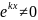 – это характеристическое уравнение.
– это характеристическое уравнение.
Если
корни действительны и различны, то
частными решениями являются
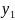 =
=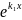 ,
,
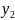 =
=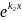 .
Общее решение y=
.
Общее решение y=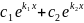
Если
корни действительные и равные, то имеет
1 частное решение
=
и
=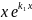
Общее
решение y=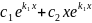
Если
корни комплексные, то частные решения
=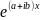 и
=
и
=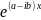
Общее
решение y=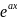 (
(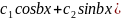
41. Неоднородные линейные дифференциальные уравнения с постоянными коэффициентами.
Уравнение вида y’’+p*y’+q*y=f(x), где p и q – некоторые числа. Общее решение уравнения представляет собой сумму общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения.
Для уравнения с постоянными коэффициентами существует следующий способ нахождения частного решения, если правая часть уравнения имеет вид:
1)
f(x)=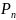 (x)*
2)f(x)=
(
(x)*cosβx+
(x)*
2)f(x)=
(
(x)*cosβx+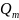 (x)*sinβx).
(x)*sinβx).
Суть метода: по виду правой части записывают ожидаемую форму частного решения с неопределенными коэффициентами, затем подставляют ее в начальное уравнение и из полученного тождества находят значения коэффициентов.
42. Системы линейных дифференциальных уравнений с постоянными коэффициентами.
Это
система вида
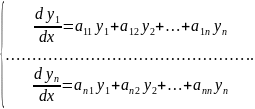
Ограничимся
системой:
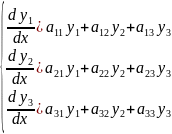 ,
где все коэффициенты постоянные.
,
где все коэффициенты постоянные.
Будем
искать частое решение в виде:
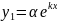 ,
,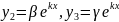 ,
где
,
где
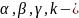 постоянные, которые надо найти. Подставим
функции в систему и сократив на множитель
получим
постоянные, которые надо найти. Подставим
функции в систему и сократив на множитель
получим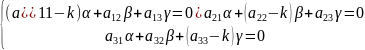
Чтобы система имела ненулевое решение, необходимо, чтобы определитель был равен 0. Далее получаем общее решение системы:
=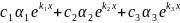 =
=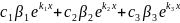
=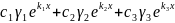
43. Понятие функций нескольких переменных. Геометрическая интерпретация.
Пусть
задано множество D
упорядоченных пар чисел (x;
y).
Соответствие f,
которое каждой паре чисел (x;
y)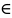 D
сопоставляет одно и только одно число
z
R,
называется функцией двух переменных,
определенной на множестве D
со значениями R
и записывается в виде z=f(x;
y).
При этом x
и y
– независимые переменные, а z
– зависимая переменная.
D
сопоставляет одно и только одно число
z
R,
называется функцией двух переменных,
определенной на множестве D
со значениями R
и записывается в виде z=f(x;
y).
При этом x
и y
– независимые переменные, а z
– зависимая переменная.
44. Предел функции двух переменных. Непрерывность.
A=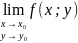 .
Функция
z
=
.
Функция
z
=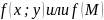 является
непрерывной в точке
является
непрерывной в точке
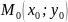 ,
если она
,
если она
1)определена в этой точке и некоторой ее окрестности
2)имеет
предел
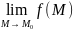
3)этот
предел равен значению функции z
в точке
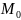 ,
т.е.
,
т.е.
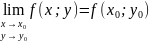
45. Понятие частной производной. Геометрический смысл.
Пусть задана функция z = f (x; y). Так как x и y – независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной х приращение ∆х, сохраняя значение y неизменным. Тогда z получит приращение, которое называется частным приращением z по x и обозначается ∆хz.
Если
существует предел
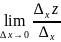 =
=
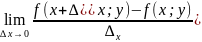 ,
то он называется частной производной
функции z=f(x;
y)
в точке M(x;
y)
по переменной х.
,
то он называется частной производной
функции z=f(x;
y)
в точке M(x;
y)
по переменной х.
Геометрический
смысл: графиком функции двух переменных
является некоторая поверхность,
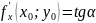 ,
где
,
где
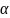 – угол между осью Ох и касательной.
– угол между осью Ох и касательной.
