1.Теорема Лагранжа;

Теорема 25.3 (Лагранж). Если функция ƒ(х) непрерывна на отрезке [а;b], дифференцируема на интервале (α;b), то найдется хотя бы одна точка сє(a;b) такая, что выполняется равенство

 

ƒ(b)-ƒ(a)=ƒ'(с)(b-a).                                      (25.2)

▼ Решение: Теорему Лагранжа можно рассматривать как частный случай теоремы Коши. Действительно, положив φ(х)=х, находим φ(b)-φ(a)=b-a, φ'(х)=1, φ'(с)=1.

Подставляя эти значения в формулу

получаем

или ƒ(b)-ƒ(a)=ƒ'(с)(b-a) ▲.

Полученную формулу называют формулой Лагранжа или формулой о конечном приращении:  приращение дифференцируемой функции на отрезке [a;b] равно приращению аргумента, умноженному на значение производной функции в некоторой внутренней точке этого отрезка

Теорема Лагранжа имеет простой геометрический смысл. Запишем формулу (25.2) в виде

 ,

 где α<с<b. Отношение   есть угловой коэффициент секущей АВ, а величина ƒ'(с) — угловой коэффициент касательной к кривой в точке с абсциссой х=с.

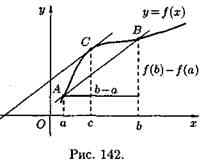
Следовательно, геометрический смысл теоремы Лагранжа таков: на графике функции y=f(x) найдется точка С(с;ƒ(с)) (см. рис. 142), в которой  касательная к графику функции параллельна секущей АВ.

 

 Следствие 25.1. Если производная функции равна нулю на некотором промежутке, то функция постоянна на этом промежутке.

Пусть ƒ'(х)=0 для  xє(α;b). Возьмем произвольные x₁ и х₂ из (а;b) и пусть x₁<х₂. Тогда по теореме Лагранжа  сє(х₁;х₂) такая, что ƒ(х₂)-f(x₁)=ƒ'(с)(х₂-х₁). Но по условию ƒ'(х)=0, стало быть, ƒ'(с)=0, где х₁<с<х₂. Поэтому имеем ƒ(х₂)-ƒ(х₁)=0, т. е. ƒ(х₂)=f(x₁). А так как x₁ и х₂ — произвольные точки из интервала (α;b),то  x є (а;b) имеем ƒ(х)≈с.

 

Следствие 25.2. Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое.

Пусть f₁' (x)=f₂^'(x) при хє(α;b). Тогда (f₁(x)-f₂(x))'=f₁'(x)-f₂'(x)=0. Следовательно, согласно следствию 25.1, функция f₁(х)-f₂(x) есть постоянная, т. е. f₁(x)-f₂(x)=C для  xє(α;b).

<< Пример 25.1

Доказать, что arcsinx + arccosx = /2, где х є [-1;1].

Решение: Пусть ƒ(х)=arcsinx+arccosx. Тогда  xє(-1;1) имеем

Отсюда следует, что ƒ(х)=С, т.е. arcsinx+arccosx=С. Положив х=0, находим 0+ /2=С, т. е. С= /2. Поэтому arcsinx+arccosx= /2. Это равенство выполняется и при х=±1 (проверьте!).

Аналогично доказывается, что arctgх+arcctgх= /2.

Формуле Лагранжа можно придать другой вид. Применив теорему Лагранжа к отрезку [х;х+∆х] (∆х>0), будем иметь

ƒ(х+∆х)-ƒ(х)=ƒ'(с)∆х.                                 (25.3)

Каждое число сє(х;х+∆х) можно записать в виде с=х+θ∆х, где 0<θ<1 (действительно, х<с<х+∆х  0<с-х<∆х  0< <1; положим    =θ   с=х+θ∆х). Формула (25.3) примет вид

ƒ(х+∆х)-ƒ(х)=ƒ'(х+θ∆х)∆х,  где 0<θ<1.

Используя теорему Лагранжа, можно оценить точность приближенного равенства ∆у≈dy. Сделаем это, считая, что функция ƒ(х) имеет непрерывную вторую производную ƒ"(х):

∆у-dy=(ƒ(х+∆х)-ƒ(х))-ƒ'(х)∆х=ƒ'(с)∆х-ƒ'(х)∆х=(ƒ'(с)-ƒ'(х))∆х=ƒ"(c₁)(c-х)∆х,

где с₁є(х;с) (рис. 143).

Итак,    ∆у-dy=f"(c₁)(c-х)∆х.    Пусть   

Так как |с-х|<∆х, a ƒ"(c₁)≤M, то получаем оценку |∆у-dy|≤М|∆х|².