
Если функция
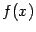 дифференцируема при всех
дифференцируема при всех
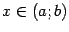 ,
то мы можем рассмотреть функцию
,
то мы можем рассмотреть функцию
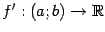 ,
сопоставляющую каждой точке
,
сопоставляющую каждой точке
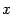 значение производной
значение производной
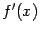 .
Эта функция
.
Эта функция
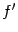 называется производной функции
называется производной функции
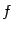 ,
или первой производной от
.
Функция
,
или первой производной от
.
Функция
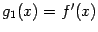 ,
в свою очередь, может иметь производную
во всех (или некоторых) точках
интервала
,
в свою очередь, может иметь производную
во всех (или некоторых) точках
интервала
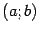 ,
которую мы обозначим
,
которую мы обозначим
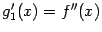 и назовём второй производной функции
.
Если предположить, что вторая производная
и назовём второй производной функции
.
Если предположить, что вторая производная
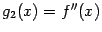 существует во всех точках
,
то она может также иметь производную
существует во всех точках
,
то она может также иметь производную
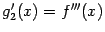 ,
называемую третьей производной функции
,
и т. д. Вообще, n-й
производной
функции называется производная от
предыдущей,
,
называемую третьей производной функции
,
и т. д. Вообще, n-й
производной
функции называется производная от
предыдущей,
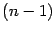 -й
производной
-й
производной
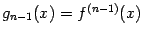 :
:
![]()
Смотри тетрадь
Смотри тетрадь
Смотри тетрадь
Смотри тетрадь
Смотри тетрадь
Смотри тетрадь
Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке (х0, у0) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х0, у0) к точке (х0+Dх, у0+Dу).
Эту главную часть приращения функции, пропорциональную приращению аргумента, называют дифференциалом функции и обозначают символом dy: dy=y/x
Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
??????????????????????????????????????????
Дифференциал функции
![]() в точке
в точке
![]() имеет вид:
имеет вид:
![]()
где
![]() — дифференциал тождественного отображения
— дифференциал тождественного отображения
![]() :
:
![]()
Пусть теперь
![]() Тогда
Тогда
![]() ,
и согласно цепному правилу:
,
и согласно цепному правилу:
![]()
Таким образом, форма первого дифференциала остаётся одной и той же вне зависимости от того, является ли переменная функцией или нет.
Дифференциал высшего порядка функции одной переменной
Для функции, зависящей
от одной переменной
![]() второй и третий дифференциалы выглядят
так:
второй и третий дифференциалы выглядят
так:
![]()
![]()
Отсюда можно вывести общий вид дифференциала n-го порядка от функции :
![]()
При вычислении дифференциалов
высших порядков очень важно, что
![]() есть произвольное и не зависящее от
есть произвольное и не зависящее от
![]() ,
которое при дифференцировании по
следует рассматривать как постоянный
множитель.
,
которое при дифференцировании по
следует рассматривать как постоянный
множитель.
Дифференциал высшего порядка функции нескольких переменных
Если функция
![]() имеет непрерывные частные производные
второго порядка, то дифференциал второго
порядка определяется так:
имеет непрерывные частные производные
второго порядка, то дифференциал второго
порядка определяется так:
![]() .
.
![]()
![]()
![]()
![]()
Символически общий вид
дифференциала n-го порядка от функции
![]() выглядит следующим образом:
выглядит следующим образом:
![]()
где
![]() ,
а
,
а
![]() произвольные приращения независимых
переменных
произвольные приращения независимых
переменных
![]() .
.
Приращения рассматриваются как постоянные и остаются одними и теми же при переходе от одного дифференциала к следующему. Сложность выражения дифференциала возрастает с увеличением числа переменных.
Если указано правило, согласно которому с каждой точкой М плоскости (или какой-нибудь части плоскости) сопоставляется некоторое число u, то говорят, что на плоскости (или на части плоскости) «задана функция точки»; задание функции символически выражается равенством вида u=f(M). Число u, сопоставляемое с точкой М, называется значением данной функции в точке М. Например, если А - фиксированная точка плоскости, М - произвольная точка, то расстояние от А до М есть функция точки М. В данном случае f(m)=AM.
С помощью таблиц, в которых указывается зависимость между значениями агрумента и значениями функции, такой способ подходит для функций, у которых аргумент принимает небольшое количество значений. Так в следующей таблице описана функция, которая показывает зависимость количества пылесосов, выпущенных заводом в зависимости от номера месяца
С помощью графиков
С помощью формулы- это наиболее распространенный способ.
Как было сказано выше, наиболее распространенным способом задания функции, является задание функции с помощью формулы. Формула позволяет для любого значения аргумента находить соответствующее значение функции путем вычислений.
Линией уровня функции двух переменных называется геометрическое место точек, в которых функция принимает одно и то же значение. Линии уровня функции z = f(x, y) определяются уравнением f(x, y)=const.
Если существует конечный предел отношения частного приращения по x функции f(x,y,z) в точке M0(x0,y0,z0) к вызвавшему его приращению Δx при Δx 0, то этот предел называется частной производной по х функции u=f(x,y,z) в точке М0.
Градиент (от лат. gradiens, род. падеж gradientis — шагающий) — характеристика, показывающая направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой. Например, если взять высоту поверхности Земли над уровнем моря (2-мерное пространство), то её градиент в каждой точке поверхности будет показывать «в горку».
Для любого постоянного числа и скалярных полей справедливо следующее:
![]()
Линейность
![]()
![]()
Правило Лейбница
![]() ,
где
,
где
![]() — скалярное произведение векторов
— скалярное произведение векторов
![]() и
и
![]() .
.
Пусть задана функция f(x, y). Тогда каждая из ее частных производных(если они, конечно, существуют)
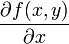 и
и
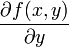 ,
которые называются также частными
производными первого порядка, снова
являются функцией независимых переменных
x, y и может, следовательно также иметь
частные производные. Частная производная
,
которые называются также частными
производными первого порядка, снова
являются функцией независимых переменных
x, y и может, следовательно также иметь
частные производные. Частная производная
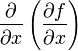 обозначается через
обозначается через
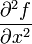 или
или
 ,
а
,
а
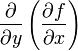 через
через
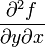 или
или
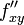 .
Таким образом,
.
Таким образом,
 ,
,
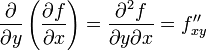
и, аналогично,
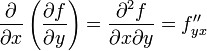 ,
,
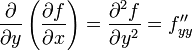 .
.
Производные
![]() и называются частными производными
второго порядка. Определение:Частной
производной второго порядка от функции
z=f(x;y) дифференцируемой в области
D,называется первая производная от
соответствующей частной производной.
Рассматривая частные производные от
них, получим всевозможные частные
производные третьего порядка:
и называются частными производными
второго порядка. Определение:Частной
производной второго порядка от функции
z=f(x;y) дифференцируемой в области
D,называется первая производная от
соответствующей частной производной.
Рассматривая частные производные от
них, получим всевозможные частные
производные третьего порядка:
![]() ,
,
![]() ,
,
![]() и т. д.
и т. д.
Предположим,
что
![]() — некоторый
— некоторый
![]() -угольник,
а функция
-угольник,
а функция
![]() осуществляет конформное отображение
осуществляет конформное отображение
![]() на
на
![]() .
Тогда
можно представить в виде
.
Тогда
можно представить в виде
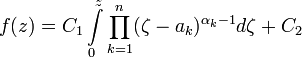 ,
,
где
![]() — прообразы вершин
на вещественной оси,
— прообразы вершин
на вещественной оси,
![]() — радианные меры соответствующих
внутренних углов, деленные на
— радианные меры соответствующих
внутренних углов, деленные на
![]() (то есть, развернутый угол соответствует
нулевой степени), а
(то есть, развернутый угол соответствует
нулевой степени), а
![]() и
и
![]() — так называемые акцессорные параметры.
Интеграл в правой части имеет собственное
название — его называют интегралом
Шварца — Кристоффеля I рода.
— так называемые акцессорные параметры.
Интеграл в правой части имеет собственное
название — его называют интегралом
Шварца — Кристоффеля I рода.
В случае, если прообраз одной из вершин многоугольника находится в бесконечности, то формула немного видоизменяется. Если -ая вершина имеет своим прообразом бесконечно удалённую точку, то формула будет иметь вид
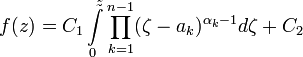 ,
,
то есть множитель, соответствующий этой вершине, будет просто отсутствовать. Такой интеграл будет интегралом Шварца — Кристоффеля II рода.
Трудность использования этих формул состоит в том, что точки , как и акцессорные параметры, в общем случае неизвестны. Для их вычисления обычно на многоугольник накладываются какие-то дополнительные нормировки, либо вычисление производится приближённо (что применяется на практике).
↑
Говорят, что функция
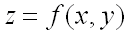 имеет максимум в точке
имеет максимум в точке
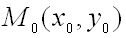 ,
т.е. при
,
т.е. при
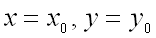 ,
если
,
если
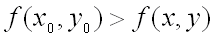 для всех точек
для всех точек
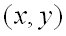 ,
достаточно близких к точке
,
достаточно близких к точке
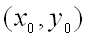 и отличных от неё.
и отличных от неё.
Говорят,
что функция
имеет минимум в точке
,
т.е. при
,
если
![]() для всех точек
,
достаточно близких к точке
и отличных от неё.
для всех точек
,
достаточно близких к точке
и отличных от неё.
Максимум и минимум функции называются экстремумами функции.
Теорема
(необходимое условие
экстремума функции двух переменных).
Если функция
достигает экстремума при
,
то каждая частная производная первого
порядка от
![]() или обращается в нуль при этих значениях
аргументов, или не существует.
или обращается в нуль при этих значениях
аргументов, или не существует.
Теорема (достаточное условие экстремума функции двух переменных). Пусть в некоторой области, содержащей точку функция имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка является критической точкой функции
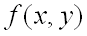 ,
т.е.
,
т.е.
![]() ,
,
тогда при :
1)
имеет максимум, если дискриминант
![]() и
и
![]() ,
где
,
где
![]() ;
;
2)
имеет минимум, если дискриминант
и
![]() ;
;
3)
не имеет ни минимума, ни максимума, если
дискриминант
![]() ;
;
4)
если
![]() ,
то экстремум может быть, а может и не
быть (требуется дополнительное
исследование).
,
то экстремум может быть, а может и не
быть (требуется дополнительное
исследование).
Первообра́зной или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
Так,
например, функция
![]() является первообразной
является первообразной
![]() .
Так как производная константы равна
нулю,
.
Так как производная константы равна
нулю,
![]() будет иметь бесконечное количество
первообразных; таких как
будет иметь бесконечное количество
первообразных; таких как
![]() или
или
![]() … и т. д.; таким образом семейство
первообразных функции
можно обозначить как
… и т. д.; таким образом семейство
первообразных функции
можно обозначить как
![]() ,
где C — любое число. Графики таких
первообразных смещены вертикально
относительно друг друга, и их положение
зависит от значения C.
,
где C — любое число. Графики таких
первообразных смещены вертикально
относительно друг друга, и их положение
зависит от значения C.
Неопределённый
интегра́л для функции
![]() — это совокупность всех первообразных
данной функции.
— это совокупность всех первообразных
данной функции.
Если
функция
определена и непрерывна на промежутке
![]() и
и
![]() — её первообразная, то есть при
— её первообразная, то есть при
![]() ,
то
,
то
![]()
где С — произвольная постоянная.
![]()
![]()
![]()
![]()
Если
![]() ,
то и
,
то и
![]() ,
где
,
где
![]() — произвольная функция, имеющая
непрерывную производную
— произвольная функция, имеющая
непрерывную производную
Свойства первообразных и неопределённого интеграла вытекают из определения и соответствующих свойств производных.
1. Из определения вытекает, что
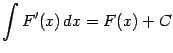
и
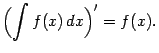
Второе равенство нужно понимать так, что производная любой из функций, составляющих неопределённый интеграл, даёт один и тот же результат, равный подынтегральной функции (это как раз и есть определение первообразной). Два написанных равенства выражают взаимную обратность операций дифференцирования и интегрирования.
2. Имеет место равенство:
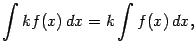
где
![]() -- произвольная постоянная. Для
доказательства обозначим через
-- произвольная постоянная. Для
доказательства обозначим через
![]() некоторую первообразную для
,
а через
некоторую первообразную для
,
а через
![]() -- некоторую первообразную для
-- некоторую первообразную для
![]() .
Тогда равенство означает, что
.
Тогда равенство означает, что
![]() , где
, где
![]() -- постоянная. Это равенство верно,
поскольку производные левой и правой
частей дают одно и то же:
-- постоянная. Это равенство верно,
поскольку производные левой и правой
частей дают одно и то же:
![]() ,
так как
-- первообразная для
,
а
,
так как
-- первообразная для
,
а
![]() , так как постоянный множитель можно
вынести за знак производной и
, так как постоянный множитель можно
вынести за знак производной и
![]() .
.
Итак, постоянный множитель можно вынесить за знак интеграла.
3. Интеграл от суммы равен сумме интегралов:
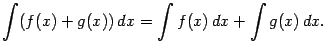
Действительно,
пусть первообразная для
равна
, для
![]() равна
, а для
равна
, а для
![]() равна
равна
![]() .
Тогда равенство означает, что
.
Тогда равенство означает, что
![]()
где
![]() .
Поскольку
.
Поскольку
![]()
и
![]()
то равенство верно; при этом мы воспользовались тем, что производная суммы равна сумме производных.
Свойства
2 и 3 называются свойствами линейности
неопределённого интеграла. Из них
следует, что для любых постоянных
![]() и
и
![]()

и, в частности,
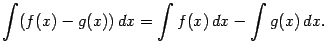
Более традиционный подход к аналитическим функциям основан на понятии производной. Из математического анализа берется элементарное определение производной и ставится вопрос, может ли функция F иметь комплексную производную Fў, задаваемую такой же формулой, как в анализе
Свойство инвариантности формул интегрирования
Всякая
формула интегрирования (см. таблицу)
сохраняет свой вид при подстановке
вместо независимой переменной любой
дифференцируемой функции, то есть если
![]() где
где
![]() то
то
![]() где
где
![]() – любая дифференцируемая функция.
– любая дифференцируемая функция.
Так,
например, если
![]() ,
то
,
то
![]() где
где
![]() – функция от
– функция от
![]()
