6. Линии и поверхности 2-го порядка. Классификация линий. Теорема о подобии линий 2-го порядка.

Мн-во всех т-к прокт-ой пл-ти, корд. кот. удовл-ют в некотором репере R(А₁,А₂,А₃,Е) Ур-ю 2-й степени =0=а₁₁х₁²+ а₂₂х₂²+ а₃₃х₁₃²+2 а₁₂ х₁х₂+2 а₁₃ х₁х₃+2 а₂₃ х₂х₃=0 наз. ЛВП, причем а_ij≠0 одновр-но. Ранг квадр-ой формы наз. рангом ЛВП. Лиин. наз. невырожд-ой, если ее r=3, вырожд-ой, если ее r<3. Лемма:Любая прямая пересекает невырожд-ую ЛВП не более, чем в 2-х точках. Д-во(м.о.п.) Пусть пр-я имеет с ЛВП 3 общ. точки М₁,М₂,М₃. Зададим репер R= [А₁,А₂,А₃,Е] след. образом: А₁= М₁(1;0;0), А₂= М₂(0;1;0), А₃= М₃(1;1;0) . А₃

Подставл. эти корд. в Ур-ие ЛВП

М₁: а₁₁=0, М₂: а₂₂=0, М₃: а₁₁+ а₂₂+ 2а₁₂=0

ЛВП примет след. вид. а₃₃х₃²+2 а₁₃ х₁х₃+ Е

+ 2 а₂₃ х₂х₃=0.

Найдем ранг:

(М₁) А₁ Е₃ (М₃₎ А₂ (М₂₎

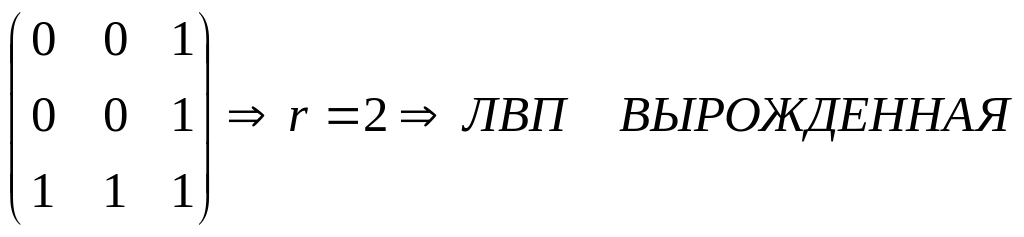
Это противоречит усл-ю леммы , след. наше предпол. неверно и и пр. 2-х т-к перес-я.Проект-ая класифик. ЛВП: изв-о, что всегда сущ. базис, в котор. квадр. формула им-ет норм. вид: ε₁х₁²+ ε₂х₂²+ ε₃х₃²=0, где ε_1,2,3=±1, r=0, поэтому м-о выделить следующие виды: 1. r=3, х₁²+ х₂²+ х₃²=0 – нулевая линия (ε_1,2,3=1); х₁²+ х₂²- х₃²=0 – овальная линия (ε_1,2,3=-1); 2. r=2, х₁²+ х₂²=0 – пара мнимых перес. прям; х₁²- х₂²=0 – пара действит. перес. прям.; 3. r=1, х₁²=0 – пара совпав. прям. Пусть задана невыр-ая ЛВП и прям., прох-ая ч-з точки Р (р₁,р₂,р₃) и Q(q₁,q₂,q₃).

В рез-те преобр-ий получ. ур-ие вида: А₁₁λ²+2 А₁₁λμ+ А₂₂μ²=0, А₁₁=∑а_ijp_ip_j , А₁₂=∑а_ijp_iq_j , А₂₂=∑а_ijq_iq_j . В завис. от D ур-ия возможны след. случаи:1. D>0 прям. перес. ЛВП в 2-х т-ах. 2. D<0 прям. перес. ЛВП в 2-х комплексно-сопряж. т-ах. 3. D=0 ур-ие имеет ед-ое решение, в этом случ. прям. наз. косат. к ЛВП. Теорема: В кажд. т-е Р(р₁,р₂,р₃) невырожд. ЛВП сущ. ед-ая касат. , задан. ур-ием: (∑а_i1p_i)х₁+(∑а_i2p_i)х₂+(∑а_i3p_i)х₃=0. Пусть задана кривая ВП и т.М не € ей.

Прям. АВ по отнош. к т.М наз. М

ее полярой, а т.М по отнош. к

АВ – полюсом. А В

Точки P и Q наз. сопряженными

отн-но ЛВП, если ∑а_ijp_iq_j=0 (1)

Пусть на проективной плоскости задана невырожд. ЛВП. Возьмем как.-нибудь т-у Р(р₁,р₂,р₃) пл-ти и рассм. мн-во q всех т-к Х(х₁,х₂,х₃), кажд. из которых сопряжена с т.Р относ. ЛВП исполь-я (1), получ. ур-е множ-ва q₃:

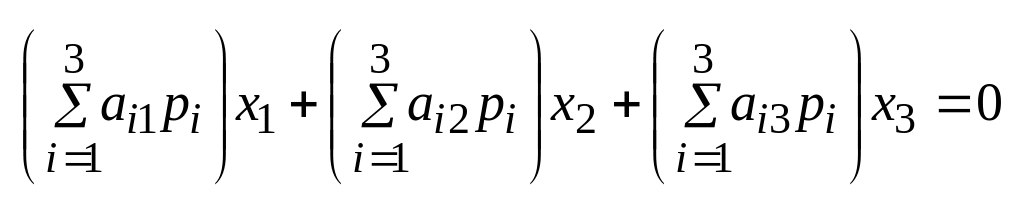(2)

В рав-ве (1) коэф. а_ij симм-ы относ. индексов i и j, т.к. а_ij= а_ji при i=1,2,3. Поэтому исполь. (1) и (2) получ. теорему: Пусть дана ЛВП. Если т.Q лежит на поляре т.Р, то т.Р лежит на поляре т.Q.