5.1. Силовой расчет быстроходного вала
Исходные данные:
l1 = 33,2 мм; l2 = 89,5 мм; l3 = LОП= 85,3 мм;
Ft1 = 4600 Н; Fr1 = 1182 Н; Fa1 = 3616 Н; Fоп = 2189 Н;
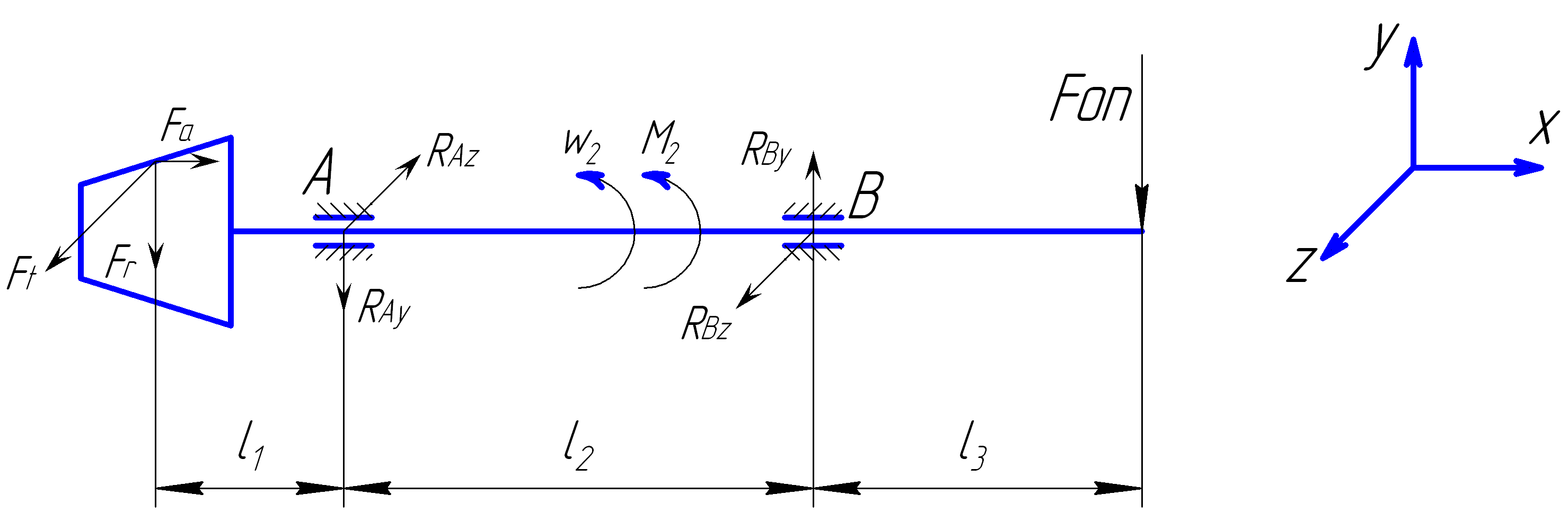
Рис.5.3. Расчетная схема быстроходного вала.
1. Плоскость XOZ
а) Определяем опорные реакции.
Составляем уравнение равновесия относительно опоры А (точка 2).
отсюда
Составляем уравнение равновесия относительно опоры В (точка 3).
отсюда
Проверка:
Значит, расчет реакций в горизонтальной плоскости произведен, верно.
б) По полученным данным строим эпюру изгибающих моментов в плоскости XOZ
2. Плоскость XOY
а) Определяем опорные реакции.
Составляем уравнение равновесия относительно опоры А (точка 2).
отсюда
Составляем уравнение равновесия относительно опоры В (точка 3).
отсюда
Проверка:
Значит, расчет реакций в вертикальной плоскости произведен, верно.
б) По полученным данным строим эпюру изгибающих моментов в плоскости XOY
3. Строим эпюру крутящих моментов:
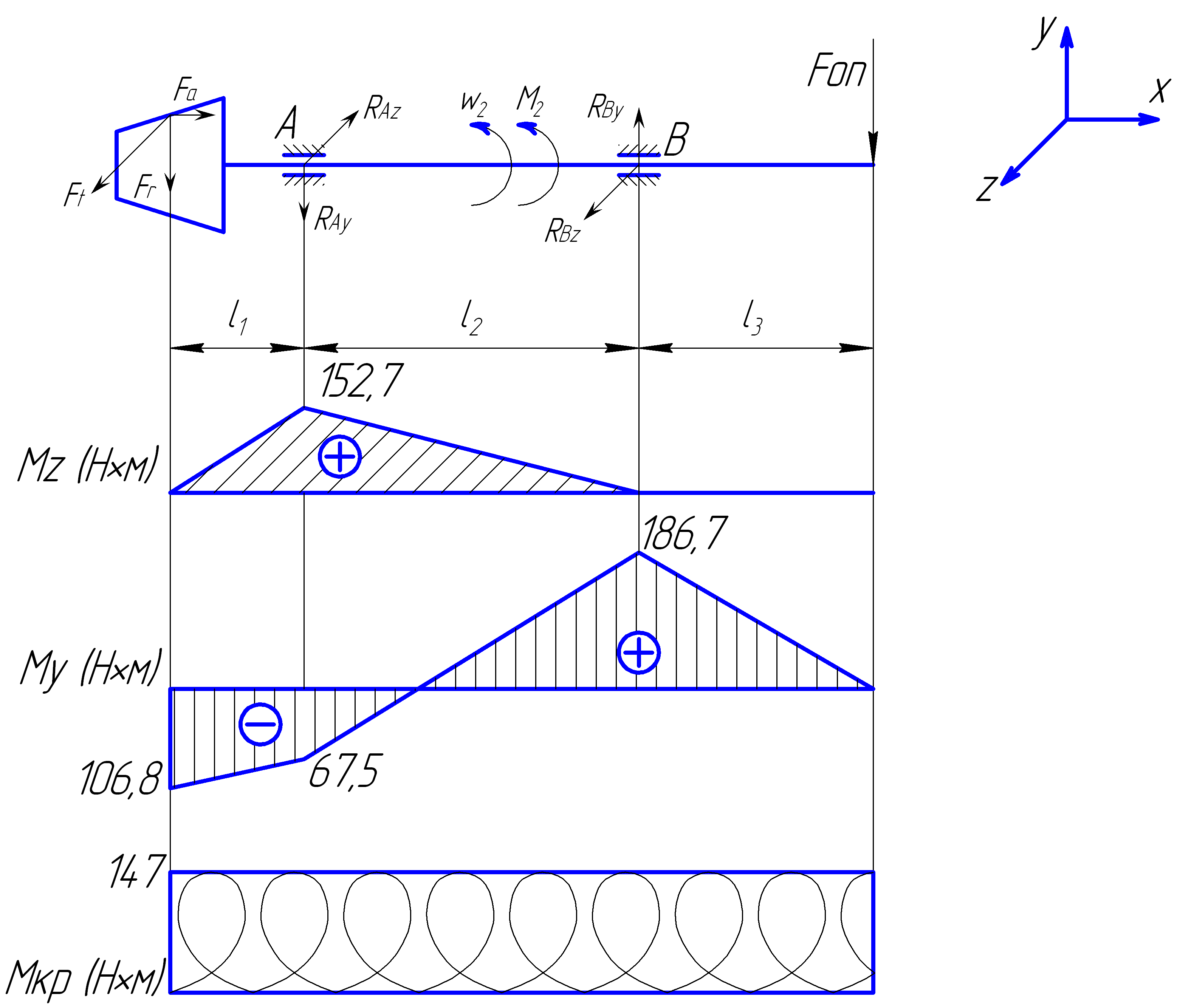
Рис. 5.4. Эпюры моментов, действующих на быстроходный вал.
4. Определяем суммарные радиальные реакции в подшипниках:
5. Определяем суммарные изгибающие моменты в наиболее нагруженных сечениях:
6. Рассчитываем составляющие реакций подшипников. Расчет проводим согласно требованиям таблицы 9.1 [ист. 4 стр. 141…142] и таблицы 9.6 [ист. 4 стр. 148].
Цифрой 2 обозначен подшипник воспринимающей осевую нагрузку в зацеплении. Наклон контактных линий в радиально-упорных подшипниках приводит к тому, что суммарные реакции в опорах подшипников, приложенные к телам качения, вызывают появление в них радиальных нагрузок Rr1 и Rr2, и их осевых составляющих RS1 и RS2, которые стремятся раздвинуть кольца подшипников в осевом направлении. Этому препятствуют буртики вала и корпуса редуктора с соответствующими реакциями Ra1 и Ra2, величина которых зависит от осевой силы в зацеплении Fa и осевых составляющих в опорах подшипников RS1 и RS2.
Находим RS1 и RS2 по формуле:
Где е = 0,42 – коэффициент влияния осевого нагружения таблица К29 [ист. 4 стр. 436…438].
Принимаем:
Находим Ra2:
Вычерчиваем схему нагружения подшипников.
Рис. 5.5. Схема нагружения подшипников быстроходного вала.
5.2. Силовой расчет тихоходного вала
Исходные данные:
l1 = 74,8 мм; l2 = 133,8 мм; l3 = 113,2 мм;
Ft2 = 4600 Н; Fr2 = 3616 Н; Fa2 = 1182 Н; Fм = 2932 Н;
Рис. 5.6. Расчетная схема тихоходного вала.
1. Плоскость XOZ:
а) Определяем опорные реакции.
Составляем уравнение равновесия относительно опоры D (точка 1).
отсюда
Составляем уравнение равновесия относительно опоры C (точка 3).
отсюда
Проверка:
Значит, расчет реакций в вертикальной плоскости произведен, верно.
б) По полученным данным строим эпюру изгибающих моментов в плоскости XOZ.
2. Плоскость XOY:
а) Определяем опорные реакции.
Составляем уравнение равновесия относительно опоры D (точка 1).
отсюда
Составляем уравнение равновесия относительно опоры C (точка 3).
отсюда
Проверка:
Значит, расчет реакций в горизонтальной плоскости произведен, верно.
б) По полученным данным строим эпюру изгибающих моментов в плоскости XOY
В точке 2 происходит скачок, на величину момента, создаваемого осевой силой:
3. Строим эпюру крутящих моментов:
Рис. 5.7. Эпюры моментов, действующих на тихоходный вал.
4. Определяем суммарные радиальные реакции в подшипниках:
5. Определяем суммарные изгибающие моменты в наиболее нагруженных сечениях:
6. Рассчитываем составляющие реакций подшипников. Расчет проводим согласно требованиям таблицы 9.1 [ист. 4 стр. 141…142] и таблицы 9.6 [ист. 4 стр. 148].
Находим RS1 и RS2 по формуле:
Где е = 0,42 – коэффициент влияния осевого нагружения таблица К29 [ист. 4 стр. 437…438].
Принимаем
Находим Ra2:
Вычерчиваем схему нагружения подшипников.
Рис. 5.8. Схема нагружения подшипников тихоходного вала.