2. Основные методы расчета линейных электрических цепей постоянного тока

В настоящей главе выводы методов расчета опущены, приведены примеры и порядок расчета.

2.1. Метод непосредственного применения законов Кирхгофа

Метод сводится к составлению системы независимых линейных алгебраических уравнений по законам Кирхгофа и ее решению относительно неизвестных. Обычно в роли неизвестных выступают токи в ветвях электрической цепи. Порядок расчета рассмотрим на примере.

Постановка задачи: задана электрическая цепь (рис. 2.1), заданы величины сопротивлений R₁- R₆, Э.Д.С. Е₁ и Е₂; требуется найти токи в ветвях I₁ – I₆.

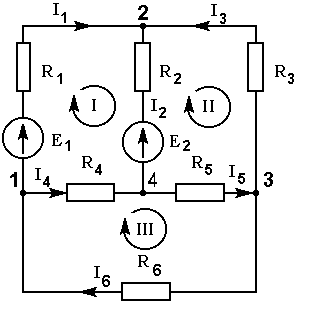
Рис. 2.1

Решение.

1. Определим число уравнений, составляемых по первому закону Кирхгофа по формуле n - 1 = 3 и по второму закону Кирхгофа по формуле m - (n - 1) = 3, где n = 4 - число узлов, m = 6 - число ветвей (рис 2.1).

2. Выбираем (произвольно) направление токов в ветвях, рис. 2.1.

3. Составляем систему из трех уравнений по первому закону Кирхгофа (для узлов 1, 2 и 3) и из трех уравнений по второму закону Кирхгофа (контуры I, II и III).

Направление обхода контуров выберем по часовой стрелке, рис. 2.1 .

Система имеет вид

-I₁ – I₄ + I₆ = 0,
I₁ – I₂ + I₃ = 0,
-I₃ + I₅ – I₆ = 0,	(2.1)
R₁I₁ + R₂I₂ – R₄I₄ = E₁ – E_2,
-R₂I₂ – R₃I₃ – R₅I₅ = E₂,
R₄I₄ + R₅I₅ + R₆I₆ = 0.

Система ( 2.1 ) может быть решена любым из известных методов расчета, например, методом подстановки или численным методом на ЭВМ. Рассмотрим решение системы с помощью ЭВМ. Приведем систему уравнений к стандартному виду:

-I₁ + 0I₂ + 0I₃ - I₄ + 0I₅ + I₆ = 0,
I₁ – I₂ + I₃ + 0I₄ + 0I₅ + 0I₆ = 0,
0I₁ + 0I₂ – I₃ + 0I₄ + I₅ – I₆ = 0,	(2.2)
R₁I₁ + R₂I₂ + 0I₃ - R₄I₄ + 0I₅ – 0I₆ = E₁ – E₂,
0I₁ – R₂I₂ – R₃I₃ + 0I₄ – R₅I₅ + 0I₆ = E₂,
0I₁ + 0I₂ + 0I₃ + R₄I₄ + R₅I₅ + R₆I₆ = 0.