1.3. Неразветвленные и разветвленные электрические цепи

Ветвь - участок цепи, образованный последовательно соединенными элементами, по которым течет один и тот же ток, и двумя узлами, рис. 1.10.

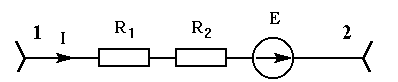
Рис. 1.10

Узел - точка цепи, в которой сходится не менее трех ветвей, обозначен на рис. 1.10 цифрами 1 и 2.

Неразветвленная электрическая цепь - это цепь, по которой течет один и тот же ток, рис. 1.11.

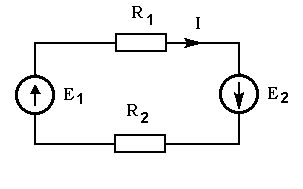
Рис. 1.11

Разветвленная электрическая цепь - это цепь, имеющая три и более ветвей, рис. 1.12.

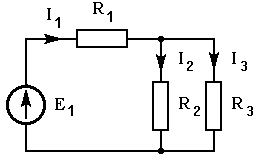
Рис. 1.12

Контур - любой замкнутый путь в электрической цепи. В неразветвленной электрической цепи один контур.

1.4. Закон Ома , законы Кирхгофа , баланс мощностей

1. Закон Ома для участка цепи записывается в виде (рис. 1.13)

I = и i = ,

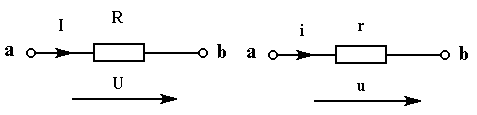
Рис. 1.13

2. Обобщенный закон Ома иллюстрируется рисунком 1.14 и следующими формулами:

.

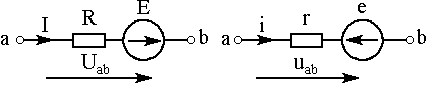
Рис. 1.14

Здесь знак у напряжения и э.д.с. берется плюс, если стрелки напряжения и э.д.с. совпадают по направлению с током, в противном случае берется знак минус.

В общем виде для цепей постоянного тока формула может быть записана

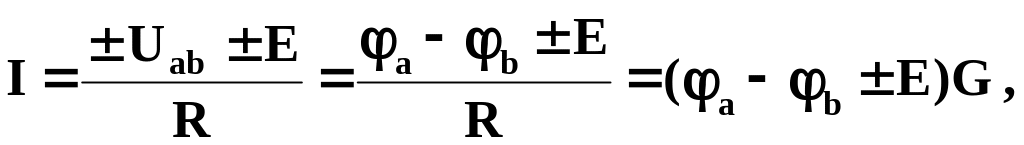
где G = - проводимость,

ток I течет от большего потенциала _a к меньшему потенциалу _b (формула записывается по обозначениям на схеме, а не по величинам потенциалов).

3. Первый закон Кирхгофа. Aлгебраическая сумма токов в любом узле электрической цепи равна нулю:

и .

4. Второй закон Кирхгофа. Для любого контура электрической цепи алгебраическая сумма падений напряжений на элементах равна алгебраической сумме э.д.с., действующих в данном контуре:

и .

Пример.

Составить уравнение по второму закону Кирхгофа для контура, показанного на рис. 1.15.

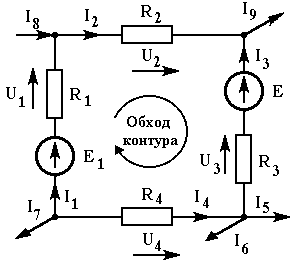
Рис. 1.15

Отметим, что стрелка падения напряжения на пассивном элементе электрической цепи совпадает по направлению с током, текущим по этому элементу (как показано на рис. 1.15).

Выбираем направление обхода контура по часовой стрелке и запишем уравнение. При этом падения напряжения, совпадающие с выбранным направлением обхода, запишем со знаком плюс, а несовпадающие с направлением обхода - со знаком минус. Затем ставим знак равенства и напишем правую часть уравнения, при этом берем э.д.с. со знаком плюс, если стрелки э.д.с. совпадают с направлением обхода, и со знаком минус, если не совпадают. Уравнение имеет вид

+U₁ + U₂ - U₃ - U₄ = +E₁ - E₃,

с учетом закона Ома уравнение может быть записано

R₁I₁ + R₂I₂ - R₃I₃ - R₄I₄ = E₁ - E₃ .

5. Баланс мощностей. Баланс мощностей вытекает из закона сохранения энергии и сводится к следующему: в любой электрической цепи сумма мощностей отдаваемой источниками энергии равна сумме мощностей потребляемой нагрузками (пассивными элементами электрической цепи).

Для цепей постоянного тока баланс мощностей может быть записан в виде

Р_и = Р_н ,

где - мощность источников; знак плюс у произведения э.д.с. на ток берется, если направления стрелок Е_к и I_к совпадают, в противном случае берется знак минус,

- мощность нагрузок.

Для цепей переменного тока баланс мощностей записывается в общем виде аналогично. Конкретные формулы будут приведены ниже. По балансу мощностей проверяется правильность расчетов электрических цепей.

Примеры составления баланса мощностей будут приведены в разделе 2 (для цепей постоянного тока) и в разделе 3 (для цепей синусоидального тока).