3.6.4. Метод двух узлов

Пример расчета, рис. 3.15 .

Дано: ₁ = 220 = 220 е ^j0 В ; ₂ = -110 - j190,53 = 220 е ^-j120 В;

₃ = -110 + j190,53 = 220 е ^j120 В; Z₁ = 15 + j15 = 21,21 е ^j45 Ом ;

Z₂ = 10 + j10 = 14,14 е ^j45 Ом; Z₃ = 20 + j20 = 28,28 е ^j45 Ом ;

Z₄ = 5 - j5 = 7,07 е ^-j45 Ом.

Найти: ₁, ₂, ₃, ₄.

Решение.

Найдем полные комплексные проводимости ветвей:

См;

См;

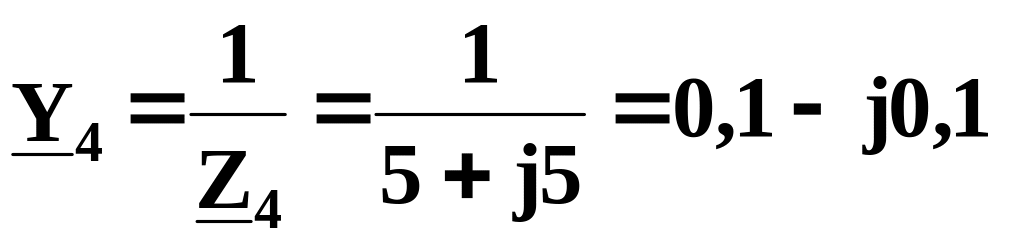См;

См.

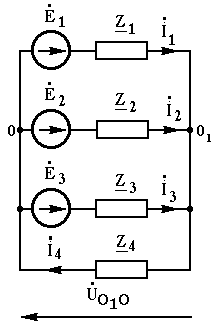
Рис. 3.15

Вычислим напряжение между двумя узлами:

В.

Определим токи с помощью обобщенного закона Ома:

1	= ( 1 - 01,0)Y1 =
	=(220 + 26,49 + j19,52)(0,03333 - j0,03333) = 8,866 - j7,565 = 11,65 e -j40,47 А;
2	= ( 2 - 01,0) Y2 =
	=(-110 - j190,53+26,49+j19,52)(0,05 - j0,05) = -12,726 - j4,375=13,46 e j198,97 А;
3	= ( 3 - 01,0) Y3 =
	=(-110+ j190,53+ 26,49+ j19,52)(0,025 - j0,025) = 3,164+ j7,339 =7,99 e j66,68 А;
4	= 01,0 Y4 = (-26,49 - j19,52)(0,1 + j0,1) = -0,697 - j4,601 = 4,653 e j81,39 А.

Проверим значение токов по первому закону Кирхгофа:

₄= ₁+ ₂+ 3= 8,866-j7,565-12,726-j4,375+3,164+j7,339 = -0,696- j4,601 А.

Тождество практически соблюдается.

Баланс мощностей:

_u = ₁I^*₁ + ₂I^*₂ + ₃I^*₃ = 220 e ^j0 11,65 e ^j40,47 +

+ 220 e ^-j120 13,46 e ^-j198,97 + 220 e ^j120 7,99 e ^-j66,68 = 5234 + j5017 ВА;

_н = Z₁I₁² + Z₂I₂² + Z₃I₃² + Z₄I₄² =

= 21,21 e ^j45 11,65² +14,14 e ^j45 13,46² + 28,28 e ^j45 7,99² +7,07 e ^{-j45 .} 4,65²

= 5232 + j5015 ВА.

Ошибки _P и _Q не превышают 5 %.

5. Метод эквивалентного генератора

Рассмотрим пример расчета, рис. 3.16 .

Рис. 3.16

Дано: ₁ = 220 = 220 e ^j0 В; Z₁ = 100 + j100 = 141,4 e ^j45 Ом;

Z₂ = 100 + j50 = 111,8 e ^j26,56 Ом; Z₃ = 100 + j50 Ом;

Z₄ = 100 + j100 Ом; Z₅ = 50 Ом.

Найти: ₅.

Решение.

1.Удалим сопротивление Z₅ и найдем э.д.с. эквивалентного генератора, равное напряжению холостого хода _ab,0 , рис. 3.17 .

По закону Ома найдем токи:

А;

А.

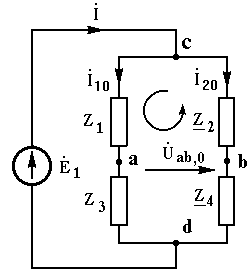
Рис. 3.17

Обойдем контур abca против часовой стрелки, тогда по второму закону Кирхгофа имеем

_ab,0 - Z_{2 20} + Z_{1 10} = 0,

затем найдем э.д.с. эквивалентного генератора:

_г= _ab,0=Z_{2 20}-Z_{1 10}=(100 + j50)(0,704-j0,528)-(100 + j100)(0,704 –

-j0,528)= -26,4 - j35,2 = 44 e ^j233,13 В.

3. Найдем сопротивление эквивалентного генератора, равного сопротивлению между точками a и b, рис. 3.18 .

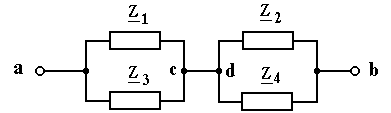
Рис. 3.18

= 104 + j72 = 126,49 e ^j34,69 Ом.

2. Используя схему эквивалентного генератора, найдем ток в пятой ветви, рис. 3.19:

А.

Рис. 3.19

5. Метод наложения

Рассмотрим пример использования метода наложения, рис. 3.20 .

Дано: ₁ = 220 e ^j0 В; ₂ = 220 e ^j0 В;

Z₁ = Z₂ = 5 + j50 = 50,25 e ^j84,3 Ом;

Z₃ = 100 - j50 = 111,8 e ^-j26,6 Ом.

Найти: ₁, ₂, ₃, _ab.

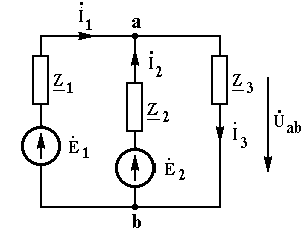
Рис. 3.20

Решение.

1. Оставим в исходной электрической цепи первую э.д.с. E₁, и найдем частичные токи '₁, '₂, '₃ и падение напряжения '_ab от этой э.д.с., рис. 3.21 .Расчет проведем по закону Ома.

Ом;

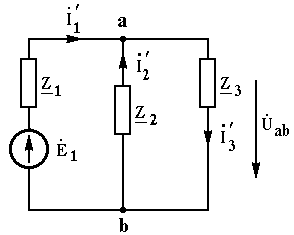
Рис. 3.21

А;

В;

А;

А.

2. Оставим в исходной электрической цепи вторую э.д.с. ₂, и определим частичные токи ₁, ₂, ₃ и падение напряжения _ab от этой э.д.с., рис. 3.22 . Для расчета воспользуемся законом Ома.

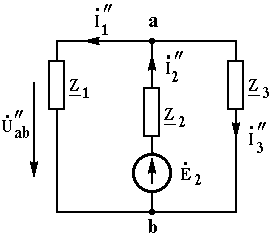
Рис. 3.22

Ом;

А;

В;

А;

А.

3. Токи в ветвях ₁, ₂, ₃ и падение напряжения _ab найдем как алгебраическую сумму соответствующих частичных токов и падений напряжения:

₁ = ₁ - ₁ = 0,73 - j2,05 + 0,28 + j2,3 = 1,01 + j0,25 = 1,04 e ^j13,9 А;

₂ = - ₂+ ₂ = 0,28 + j2,3 + 0,73 - j2,05 = 1,01 + j0,25 = 1,04 e ^j13,9 А;

₃ = ₃ + ₃ = 1,01 + j0,25 + 1,01 + j0,25 = 2,02 + j0,5 = 2,08 e ^j13,9 А;

_ab = _ab+ _ab =113,5 - j25,6 + 113,5 - j25,6= 227 - j51,2 = 232,7 e ^-j12,7 В.

4. Найденное решение проверим по балансу мощностей:

_и = ₁I^*₁ + ₂I^*₂ = 220 e ^{j0 .} 1,04 e ^-j13,9 + 220 e ^{j0 .} 1,04 e ^-j13,9 =

= 444 - j110 ВА;

_н = Z₁I₁² + Z₂I₂² + Z₃I₃² = 50,25 e ^{j84,3 .} 1,04² + 50,25 e ^{j84,3 .} 1,04² +

+ 111,8 e ^{-j26,6 .} 2,08² = 443 - j108 ВА.

меньше 5%.