3.3. Операции с комплексными числами

Рассмотрим операции с векторами и комплексными числами.

1. Сложение и вычитание производится в алгебраической форме:

= ₁ + ₂ = a₁ + jb₁ + a₂ + jb₂ = (a₁ + a₂) + j(b₁ + b₂) = a + jb;

= ₁ - ₂ = a₁ + jb₁ - (a₂ + jb₂) = (a₁ - a₂) + j(b₁- b₂) = a + jb.

Операции с векторами показаны на рис. 3.3.

Рис. 3.3 Показаны операции с векторами:

a = a₁ + a₂; a = a₁ - a₂;

b = b₁ + b₂; b = b₁ - b₂

Пример: = (5 + j7) + ( -9 + j5) = -4 + j12;

= (5 + j7) - ( -9 + j5) = 14 + j2.

2. Умножение и деление можно проводить в показательной

= _{1 2} = A₁ e ^j1A₂ e ^j2 = A₁ A₂ e ^j(1+2) = A e ^j ;

и в алгебраической формах:

= (a₁ + jb₁)(a₂ + jb₂) = (a₁a₂ - b₁b₂) + j(a₁b₂ + a₂b₁) = a + jb;

Пример: = 10 e ^{j20 .} 2 e ^-j30 = 20 e ^-j10 ;

= (2 + j3)(4 + j5) = (8 - 15) + j(10 + 12) = -7 + j22;

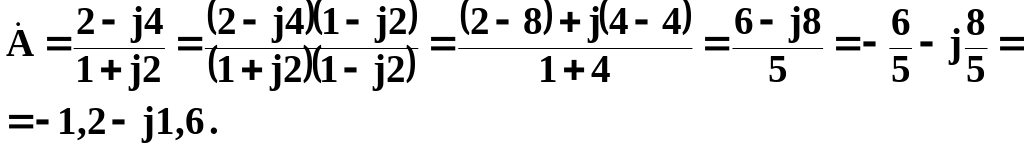
Перевод комплексного числа из алгебраической формы в показательную форму и обратно осуществляется по формулам:

1. Из алгебраической формы в показательную, рис. 3.4,

= a + jb = A e ^j ,

здесь A = , ( при этом a, b < A < a + b );

если a > 0 ( I и IV квадранты ), то

если a < 0 ( II и III квадранты), то

При этом значения вещественной а и мнимой b частей подставляются со своими знаками.

Пример: ₁ = 5 + j8 = e ^{j arctg (8/5)} = 9,43 e ^j58 ;

₂ = -5 + j8 = 9,43 e ^j122 ;

₃ = ₄ = -5 - j8 = 9,43 e ^j238 = 9,43 e ^-j122 ;

₄ = 5 - j8 = 9,43 e ^-j58 .

Векторы показаны на рис. 3.5.

Рис. 3.4 Рис. 3.5

2. Из показательной формы в алгебраическую, рис. 3.4,

= A e ^j = A cos  + jA sin  = a + jb.

Пример: ₁ = 10 e ^j30 = 10 cos30^o + j10 sin30^o = 8,66 + j5;

₂ = 220 e ^j0 = 220 + j0 = 220;

₃ = -10 e ^-j50 = -10 cos(-50^o) - j10 sin(-50^o) = - 6,43 + j7,66;

₄ = 5 e ^j210 = 5 cos210^o + j5 sin210^o = - 4,33 - j2,5.

Частные случаи:

3.4. Последовательное, параллельное и смешанное соединения элементов

Приведем формулы определения полных комплексных сопротивлений последовательного и параллельного соединения элементов.

Рассмотрим на примере электрических схем рис. 3.6 и 3.7.

Дано: Z₁ = 5 + 5j Ом, Z₂ = 3 - j8 Ом, Z₃ = -j10 Ом.

Найти: Z - полное комплексное сопротивление последовательной и параллельной цепочек.

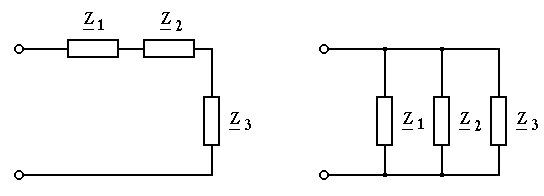
Рис. 3.6 Рис. 3.7

В общем случае для последовательно соединенных элементов

Z = Z_{к .}

Для рассматриваемого примера (рис.3.6)

Z = Z₁ + Z₂ + Z₃ = 5 + j5 + 3 - j8 - j10 = 8 - j13 Ом.

Для параллельной цепочки найдем полную комплексную проводимость и полное комплексное сопротивление:

.

Для нашего примера (рис.3.7)

См;

См;

См;

См;

Ом,

.

Рассмотрим пример расчёта электрической цепи со смешанным соединением элементов (рис. 3.8).

Дано: U = 220 B , Z₁= 5+j8 Ом, Z₂ = Z₃ = 20+j20 Ом.

Найти: ₁, ₂, _{3 .}

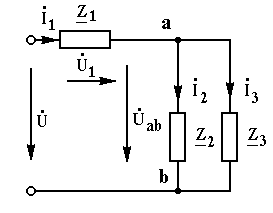
Рис. 3.8

Решение.

а) Эквивалентное сопротивление параллельного участка

Ом.

б) Полное комплексное сопротивление всей цепи

Ом.

в) Найдём токи:

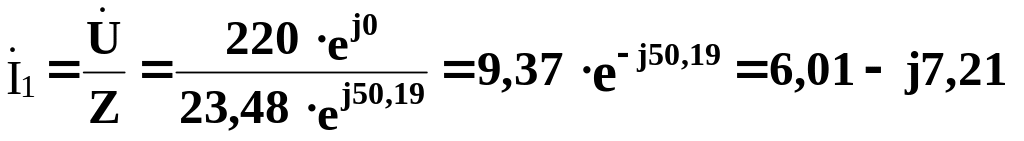А;

В;

А;

А.

г) Проверим токи по первому закону Кирхгофа ₁ = ₂ + ₃ :

₁ = 6,01 - j7,21 А; ₂ + ₃ = 2,99 - j3,58 + 2,99 - j3,58 = 5,98 - j7,16 А.

Действительные и мнимые части у ₁ и ( ₂+ ₃ ) отличаются незначительно. Будем считать, что значения токов найдены правильно.