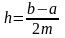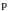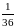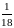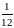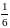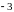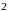Б

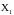Бросаются два игральных кубика. Пусть случайная величина есть число очков, выпавших на первом кубике, а случайная величина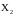 – на втором. Ряд распределения случайной величины 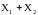имеет вид

		2	3	4	5	6	7	8	9	10	11	12

В

В интерполяционной формуле Ньютона равно -

В формуле прямоугольников для приближенного вычисления определенных интегралов 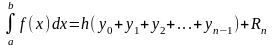шаг h вычисляется по формуле -

В приближенных вычислениях определенных интегралов наибольшую точность дает метод - Симпсона (парабол)

Вероятность того, что в результате двух испытаний 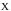хотя бы один раз примет значение, принадлежащее интервалу (0,25; 0,75) равна - 0,75.

Вероятность того, что наугад записанное четырёхзначное число окажется палиндромом равна - .

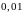В турнире участвуют 4 человека. Число способов, которыми могут распределиться места между ними, равно -

Вероятность того, что при подбрасывании двух игральных кубиков произведение выпавших очков окажется равным 6, равна - 1/9

Вероятность попадания при каждом выстреле равна .

В определении простейшего (пуассоновского) потока событий отсутствует предположение – регулярности

В цепи Маркова с дискретным временем шагами называются - моменты времени, в которые система может перейти из одного состояния в другое;

В непрерывной цепи Маркова переход системы из одного состояния в другое может произойти - в любой момент времени;

В классическом определении вероятности события пространство исходов опыта представляет собой - конечное множество

В геометрическом определении вероятности события пространство исходов опыта представляет собой - бесконечное множество

Вероятность события есть - число

Вероятность любого события принадлежит промежутку -

Вероятность невозможного события равна - 0

Вероятность достоверного события равна - 1

Вероятности событий и связаны равенством -

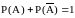
Выборка, адекватно отражающая исследуемую генеральную совокупность, называется – репрезентативной

Г

Гипотезами называются - попарно несовместные события, образующие полную группу событий;

Д

Два стрелка произвели по одному выстрелу в мишень. Вероятность попадания для 1-го стрелка равна 0,7 , для 2-го – 0,8. Математичес­кое ожидание случайной величины, значения которой равны числу попаданий в мишень равно -

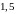
Даны законы распределения случайных величин и :

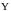	0	5	7
	0,1	0,4	0,5

	0	4	5
	0,3	0,6	0,1

Дисперсия случайной величины 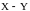равна -

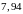
Дан закон распределения случайной величины :

	1	2	3	4
	0,3	0,4	0,2	0,1

Мода случайной величины равна - 1.

Для произвольного события и гипотез формула Байеса имеет вид -

Десять электрических лампочек включены в цепь последовательно. Если вероятность выхода из строя каждой лампочки равна 0,1, то вероятность разрыва цепи равна - .

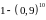Для случайной величины выборочная средняя является точечной оценкой её - математического ожидания;

Для исследуемой случайной величины гистограмма относительных частот группированной выборки является статистическим аналогом - плотности распределения вероятностей

Дан закон распределения дискретной случайной величины :

	1	2	3	4
	0,2	0,4	0,1	0,3

Вероятность 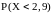равна - 0,6

Дан закон распределения дискретной случайной величины :

	0	1	2
	0,2	0,5	0,3

Дисперсия любой случайной величины обладает свойствами ( – любая константа) - и .

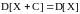Дана плотность распределения вероятностей случайной величины . Математическое ожидание и дисперсия соответственно равны - 2 и 9

Дисперсия любой случайной величины – неотрицательна

Доверительным называется интервал, который накрывает оцениваемый параметр распределения - с некоторой заданной вероятностью;

Е

Если – матрица перехода однородной цепи Маркова с дискретным временем за один шаг, то матрица перехода за два

шага есть матрица -

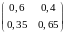
Если случайно отобранные из генеральной совокупности объекты не возвращается обратно, то получаемая выборка называется - бесповторной

Если функция распределения случайной величины X имеет вид

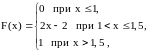
то вероятность равна - 1

Если функция распределения случайной величины имеет вид

то математическое ожидание равно - 2

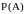Если n – число всех исходов опыта и – число исходов, благоприятствующих событию , то вероятность равна -

З

Закон распределения случайной величины может быть представлен таблицей:

		1/3	1/3	1/3

			1	2
		0,98	0,01	0,01

Закон распределения случайной величины 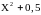имеет вид:

		0,5	1,5	4,5
		0,2	0,5	0,3

Значения, принимаемые любой непрерывной случайной величиной - заполняют некоторый интервал;

Значения, принимаемые дискретной случайной величиной - образуют конечное или счётное множество;

И

Интерполяционным многочленом Лагранжа является -

Информация отправлена от резидента в центр по трём различным каналам связи. Вероятность прохождения её по каждому из каналов оценивается соответственно в 60%, 90% и 50%. Вероятность того, что информация попадёт в центр равна - .

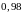Известно, что

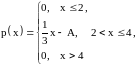
есть плотность распределения вероятностей некоторой непрерывной случайной величины.

Тогда число А равно - .

Известно, что случайная величина Х имеет нормальное распределение, причём и . Тогда с точностью до 0,0001 вероятность 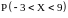равна - 0,9973

Известно, что при подбрасывании игрального кубика выпало нечётное число очков. Вероятность того, что выпало 5 очков равна – 1/3

К

Квадратная матрица с неотрицательными элементами называется стохастической, если - сумма всех элементов любой её строки равна 1;

К дискретной случайной величине относятся - пуассоновское распределение, биномиальное распределение;

К непрерывной случайной величине относится - нормальное распределение;

Комбинаторным соединением, в котором не учитывается порядок входящих в него элементов, является - сочетание

Количество обедов, которое можно составить из меню, содержащего 4 первых и 6 вторых блюд, равно – 24

Количество параметров входящих в выражение плотности вероятности случайной величины, распределённой по экспоненциальному закону, равно - один

Коэффициент корреляции между двумя случайными величинами находится в прормежутке -

Корреляционный момент (ковариация) двух независимых случайных величин может принимать значения -

М

Монета подбрасывается два раза. Ряд распределения случайной величины , значения которой равны числу выпавших гербов, имеет вид:

		0	1	2
		1/4	½	1/4

Медиана не совпадает с математическим ожиданием для - показательного закона распределения;

Марковские цепи относятся к случайным процессам - без последействия.

Математическое ожидание любой случайной величины - может быть любым действительным числом

Множество всех однотипных объектов, подлежащих статистическому анализу, называется - генеральной совокупностью

Матрица переходных вероятностей однородной цепи Маркова с дискретным временем является – стохастической

Метод простых итераций решения уравнения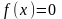 состоит в замене исходного уравнения эквивалентным ему уравнением -

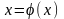
Н

Начальное приближение корня x₀ уравнения , решаемого методом Ньютона (касательных), удовлетворяет условию -

Наивероятнейшее число попаданий при 5 выстрелах равно - 1

О

Оценка 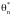параметра 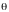распределения называется несмещённой, если -

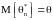
Объёмом статистической выборки называется - число составляющих её значений;

Относительной частотой события в серии испытаний называется - результат деления числа появлений события в серии на число всех испытаний серии

П

Приближенное решение уравнения методом Ньютона (касательных) производится по формуле -

Первое приближенное значение корня уравнения , изолированного на отрезке [a,b], методом хорд найдется по формуле -

При решении уравнения методом итераций функция 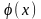должна удовлетворять условию -

По каждой из дорог, изображенных на рисунке, можно пройти лишь в одном направлении. На каждой развилке следующая дорога выбирается наугад. Вероятность, что путник, вышедший из пункта А, попадет в пункт В равна:

При решении уравнения методом проб необходимо выполнение условия -

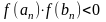
При решении уравнения 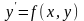методом Эйлера 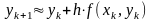, где h - шаг изменения аргумента

При решении уравнения методом Рунге-Кутта определяют k_i, где i равно - 4

При решении уравнения методом Адамса изначально находятся значения искомой функции , где n равно - 3

При вычислении определенного интеграла по формуле Симпсона шаг h находится по формуле -